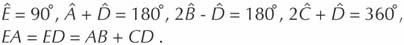Các bộ phần này gọi là các viên ngói của hình lát. Trong trường hợp khác với tập hợp một điểm, giao của hai viên ngói được gọi là cạnh của hình lát và được gọi là đỉnh của hình lát trong trường hợp ngược lại.
Đối với một hình lát P, ta kí hiệu S(P) là tập hợp các đẳng cự f của mặt phẳng sao cho ảnh của mọi viên ngói thuộc P qua f là một viên ngói của P. S(P) là một nhóm, gọi là nhóm các phép đối xứng của hình lát. Ta cần xét một số trường hợp đối với nhóm này :
• S(P) không chứa bất kì phép tịnh tiến nào. Khi đó S(P) sẽ là một đẳng cấu vào một nhóm vòng, có thể suy biến thành biến đổi đồng nhất sinh ra bởi một phép quay có góc quay là 2π/n, hoặc vào một nhóm điêđran, nhóm các phép đối xứng của đa giác đều n cạnh.
• S(P) chứa các phép tịnh tiến của các vectơ tất cả đều cộng tuyến với nhau. Khi đó S(P) là một đẳng cấu vào một trong 7 nhóm frizơ.
• S(P) chứa hai phép tịnh tiến của các vectơ không cộng tuyến. Khi đó S(P) là một đẳng cấu vào một trong 17 nhóm cristanlôgraphic và hình lát được gọi là tuần hoàn.
Nếu tất cả các viên ngói của hình lát có thể thu được nhờ một phép đẳng cự của chỉ
duy nhất một viên ngói, ta nói rằng hình lát là mônôhêđran. Ở đây ta chỉ quan tâm tới các trường hợp hình lát mônôhêđran mà ở đó các viên ngói đều là các đa giác.
Đầu tiên ta sẽ dựng một hình lát mônôhêđran mà mỗi viên lát là một tam giác bất kì. Ta dựng tam giác ABC bất kì nhờ công cụ [Đường]Tam giác, sau đó dựng điểm I là trung điểm của một cạnh, ví dụ của cạnh BC nhờ công cụ [Dựng hình]Trung điểm. Gọi D là điểm đối xứng của A qua điểm I, có được bằng công cụ [Biến hình]Đối xứng tâm bằng cách chọn đối tượng cần biến đổi là điểm A rồi sau đó chọn tâm đối xứng I.
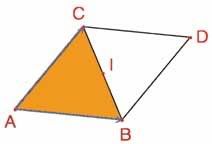
Hình 3.1 – Ta dựng hình đối xứng của tam giác ABC qua trung điểm của một trong ba cạnh của nó (ở đây là của cạnh BC). Khi đó ta thu được hình bình hành ABDC.
Tứ giác ABCD là một hình bình hành và ta có thể sử dụng nó để lát mặt phẳng. Ta dựng hai vectơ 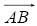 và và 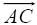 nhờ công cụ [Đường]Vectơ, và sau đó ta sự dụng chúng để nhân các tam giác ABC et BCD ra bằng phép tịnh tiến nhờ công cụ [Biến hình]Tịnh tiến. nhờ công cụ [Đường]Vectơ, và sau đó ta sự dụng chúng để nhân các tam giác ABC et BCD ra bằng phép tịnh tiến nhờ công cụ [Biến hình]Tịnh tiến.
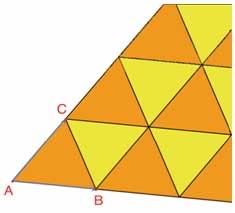
Hình 3.2 - Dựng các ảnh của hai tam giác qua các phép tịnh tiến.
Bằng cách tiến hành tương tự ta có thể lát mặt phẳng bằng một tứ giác bất kì, có thể lồi hay không nhưng không được là tứ giác chéo. Ta sẽ dựng hình đối xứng của tứ giác qua trung điểm của một cạnh và thu được một hình lục giác có các cặp cạnh đối song song từng đôi một. Lục giác này sẽ lát đầy mặt phẳng.
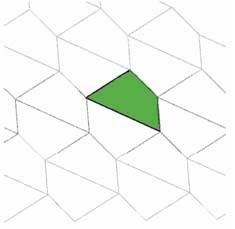
Hình3.3 - Một cách dựng tương tự cho phép lát mặt phẳng bằng một tứ giác bất kì, có thể không lồi nhưng không được tự cắt.
Đối với các đa giác lồi loại khác, bài toán trở nên phức tạp hơn. Đối với hình bẩy cạnh trở lên, ta có thể chứng minh rằng không tồn tại bất kì đa giác nào có thể lát được mặt phẳng. Có 3 loại lục giác lồi có thể lát được mặt phẳng và có ít nhất 14 loại ngũ giác lồi có thể lát được mặt phẳng, mỗi loại được xác định bởi một tập hợp các ràng buộc
về góc và về độ dài cạnh. Đối với các ngũ giác, ngày nay người ta chưa kiểm chứng được có phải 14 loại ngũ giác này cho ta toàn bộ lời giải hay không ? Loại cuối cùng được khám phá là vào năm 1985. Theo chúng tôi biết, người ta chưa có câu trả lời cho các đa giác không lồi.
Bài tập 12 - Dựng ngũ giác lồi ABCDE thoả mãn điều kiện sau : góc tại A có số đo  là 60°, góc tại C có số đo là 120°, AB = AE, CB = CD. Các điều kiện này không xác định một ngũ giác duy nhất mà xác định một họ các ngũ giác. Do đó số các điểm tự do của phép dựng sẽ ít nhất là ba.
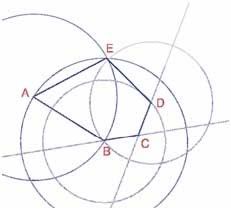
Hình 3.4 - Dựng một ngũ giác thoả mãn các điều kiện A = 60°, C = 120°, AB = AE và CB = BD. Các điểm A, B và C là các điểm tự do trong mặt phẳng.
Bằng các phép quay liên tiếp tâm A và góc quay là 60° (công cụ [Biến hình]Quay yêu cầu chọn đối tượng cần biến đổi, một góc, một tâm) ta dựng một « bông hoa » gồm 6 ngũ giác. Góc là số ta nhập vào vùng làm việc với công cụ [Văn bản và Biểu tượng]Số.
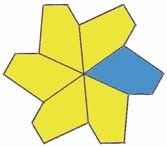
Hình 3.5 – Ngũ giác cơ sở được áp dụng cho phép quay tâm A, góc quay 60°, để thu được một « bông hoa » có sáu cánh.
Các bông hoa này có thể được nhân ra tiếp nhờ phép tịnh tiến để lát mặt phẳng. Hình lát thu được là kiểu thứ 5 trong sự xếp loại được đề cập đến trong Tilings and Patterns. Nó được công bố bởi K. Reinhardt vào năm 1918. Hình lát này không chỉ mônôhêđran, có nghĩa là tất cả các viên ngói đều trùng nhau qua một phép đẳng cự, nhưng hơn nữa nó cũng là isohêđran : tất cả các viên ngói đóng một vai trò quan trọng như nhau trong hình lát. Một cách cụ thể hơn, nếu một phép đẳng cự biến đổi một viên ngói thành một viên khác của hình lát thì nó thuộc nhóm các phép đối xứng của sự hình lát.
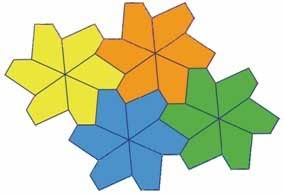
Hình 3.6 – Các bông hoa được tạo ra bởi phép tịnh tiến để phủ toàn bộ mặt phẳng
Bài tập 13* - Dựng một ngũ giác ABCDE thoả mãn các điều kiện ràng buộc :
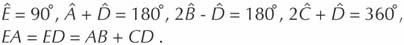
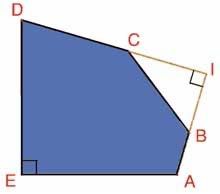
Hình 3. 7 – Ngũ giác kiểu thứ 10 theo sự xếp loại trong Tilings and Patterns. Ngũ giác này dùng trong hình lát loại mônôhêđran. Các điểm E và A là các điểm tự do trong mặt phẳng và điểm I là điểm tự do trên cung tròn.
Hình lát này được thực hiện bằng cách tạo ra ba hình từ viên ngói cơ sở bằng phép quay tâm E, góc quay 90° liên tiếp quanh đỉnh E. Sau đó các hình vuông được ghép thành các dải bởi các phép tịnh tiến theo một phương. Các dải hình vuông được phân cách bởi các dải ngũ giác như minh hoạ trong hình dưới đây.
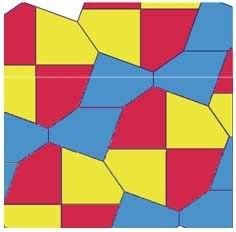
Hình 3.8 – Hình lát mônôhêđran tạo bởi các đa giác lồi. Hình lát này được sáng tạo bởi Richard E. James III sau một bài báo công bố công trình của Martin Gardner trong tạp chí Scientific American năm 1975. Ta có thể đọc bài báo này sau khi được bổ xung trong tạp chí Time travel and other mathematical bewilderments của Martin Gardner, Nhà xuất bản Freeman 1987.
School@net
|

 Ta sẽ dựng một số hình lát của mặt phẳng bằng các đa giác. Ta sẽ bắt đầu bằng một số định nghĩa đơn giản nhưng đủ dùng cho sau này. Bạn đọc quan tâm có thể tham khảo thêm quyển sách kinh điển về vấn đề này « Tilings and Patterns » của Branko Grünbaum và G.C. Shephard, Nhà xuất bản Freeman 1987. Ta cũng có thể tìm được một số lượng lớn các trang WEB về các hình lát cũng như về các nhóm đối xứng.
Ta sẽ dựng một số hình lát của mặt phẳng bằng các đa giác. Ta sẽ bắt đầu bằng một số định nghĩa đơn giản nhưng đủ dùng cho sau này. Bạn đọc quan tâm có thể tham khảo thêm quyển sách kinh điển về vấn đề này « Tilings and Patterns » của Branko Grünbaum và G.C. Shephard, Nhà xuất bản Freeman 1987. Ta cũng có thể tìm được một số lượng lớn các trang WEB về các hình lát cũng như về các nhóm đối xứng.
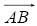 và
và 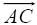 nhờ công cụ [Đường]Vectơ, và sau đó ta sự dụng chúng để nhân các tam giác ABC et BCD ra bằng phép tịnh tiến nhờ công cụ [Biến hình]Tịnh tiến.
nhờ công cụ [Đường]Vectơ, và sau đó ta sự dụng chúng để nhân các tam giác ABC et BCD ra bằng phép tịnh tiến nhờ công cụ [Biến hình]Tịnh tiến.