Tôi không cần những cách dựng ra sao, tôi cũng không cần hình vẽ trình diễn đẹp hay xấu như thế nào. Tôi chỉ muốn biết được bản chất của cách dựng là gì. Đây, theo tôi là một điều cần đặc biệt lưu ý. Trong đời sống, nếu như chúng ta không tỉnh thì chúng ta sẽ bị rơi vào sự điều khiển của người khác mà chúng ta không hay. Trong khoa học cũng vậy, nếu bạn không thực sự tỉnh táo thì bạn cũng rơi vào sự điều khiển của khoa học. Nếu bạn bắt chước và cứ bắt chước hoài thì bạn sẽ thật sự rơi vào tình trạng làm nô lệ cho khoa học lúc nào không biết. Những hình vẽ của người khác trình diễn cho bạn thực sự gây ấn tượng cho bạn. Thậm chí người ta cho bạn tất cả những hình vẽ, bày cho bạn tất cả kĩ thuật vẽ, nhưng bản chất của nó bạn không biết thì bạn chỉ suốt đời làm con rối cho họ mà thôi. Từ bài báo này, tôi sẽ trình bày tất cả cơ sở toán mà tôi cho là quan trọng nhất. Trước hết là phép dựng elip.
Trong tất cả các phần mềm hình học động, cơ sở toán của phép dựng ba đường cônic là một trong những bản lề của các phép dựng hình. Lẽ dĩ nhiên, bản chất của những phép dựng quan trọng như vậy không ai cho bạn biết cả đâu. Bởi một khi bạn biết rồi, thì coi như họ trắng tay. Khi tôi công bố các bài viết này, thì tôi thực sự đã tặng cho các bạn những con gà đẻ trứng vàng. Bởi từ cơ sở toán này, bạn sẽ dựng được hàng trăm, hàng nghìn hình vẽ trên các phần mềm hình học động và đó là những cái do chính các bạn làm ra. Liệu những cơ sở toán này, tôi là người biết đầu tiên ? Câu trả lời chắc chắn là không ! Tuy nhiên, tôi là người dám hy sinh vì lợi ích cá nhân cho khoa học. Tôi sẵn sàng tặng hết những gì tôi biết được cho khoa học. Tôi không sử dụng dụng nó làm bí mật riêng cho mình để trục lợi vì bất cứ mục đích gì.
Trong tất cả các phần mềm hình học động như Cabri, Sketchpad thì luôn có nút lệnh cônic. Muốn dựng được cônic thì bạn phải biết được 5 điểm : A, B, C, D, E. Vậy thì vì sao một cônic lại dựng được khi biết 5 điểm ? Câu trả lời cho vấn đề này có nhiều. Chúng ta hãy bắt đầu với việc giải thích như sau :
Cách 1. Ta chọn hệ trục toạ độ Oxy trong mặt phẳng, ta đã biết phương trình tổng quát của đường bậc hai là :
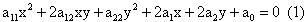
Trong đó
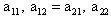
không đồng thời bằng 0.
Ta biết rằng có hệ toạ độ Descartes vuông góc ΩXY để phương trình bậc hai trên có một và chỉ một trong chín dạng đơn giản sau đây chính là
phương trình dạng chính tắc của đường bậc hai đó.
Xét các bất biến:
 1). Nếu
1). Nếu 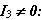 : Đường bậc hai không suy biến.
: Đường bậc hai không suy biến.
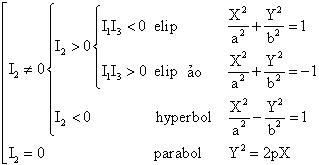 2). Nếu I3 = 0: Đường bậc hai suy biến.
2). Nếu I3 = 0: Đường bậc hai suy biến.

Như vậy, phương trình (1) luôn xác định một cônic (elip, hyperbol hay parabol) và các trường hợp suy biến.
Dựa vào điều kiện:
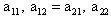
không đồng thời bằng 0, nên có ít nhất một giá trị khác 0 ; giả sử
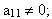
chia hai vế của (1) cho a11 ta được một phương trình có dạng như sau:
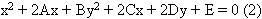
Thay toạ độ của 5 điểm xác định cônic vào (2) ta được một hệ phương trình tuyến tính chứa 5 ẩn A, B, C, D, E. Giải hệ phương trình đó sẽ xác định được một cônic và các trường hợp suy biến của nó. Vậy một cônic hoàn toàn xác định khi biết 5 điểm.
Cách 2. Ta có thể sử dụng kiến thức của hình học Xạ ảnh để giải thích cho vấn đề này.
‘‘Cho bất cứ năm điểm nào trong mặt phẳng, bao giờ cũng có một cônic thuộc 5 điểm đó. Cônic này là duy nhất trừ trường hợp trong năm điểm có ít nhất bốn điểm thẳng hàng’’.
Ta chứng minh như sau. Ta xét các trường hợp :
1) Năm điểm thẳng hàng : Ta có vô số cônic thuộc năm điểm đó, mỗi cônic suy biến thành một cặp đường thẳng trong đó một đường có thể lấy tuỳ ý còn đường kia là đường thuộc năm điểm đã cho.
2) Bốn điểm thẳng hàng : Lúc này, mỗi cặp đường thẳng gồm đường thẳng thuộc bốn điểm này và bất cứ đường thẳng nào thuộc điểm thứ năm đều là một cônic suy biến thuộc cả 5 điểm.
3) Ba điểm thẳng hàng : Lúc này cặp đường thẳng gồm có đường thẳng thuộc ba điểm này và đường thẳng thuộc hai điểm còn lại là cônic suy biến duy nhất thuộc cả năm điểm.
4) Không có ba điểm nào thẳng hàng. Giả sử năm điểm là A, B, C, D, E. Lúc này có một ánh xạ cộng tuyến duy nhất trong đó có các tia AC, AD, AE theo thứ tự ứng với các tia
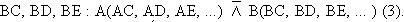
Và ánh xạ cộng tuyến này xác định một cônic không suy biến thuộc A, B, C, D, E. Cônic này là duy nhất vì (3) là duy nhất.
Sau khi đã có tường tận cơ sở toán của phép dựng cônic. Ta đi tìm hiểu cơ sở toán của elip.
Để dựng được elip trên phần mềm hình học động, chúng ta có nhiều cách dựng. Mỗi cách dựng đều có cơ sở toán tương ứng. Ta hãy đến với một số cách dựng elip sau :
Cách 1. Dựng Cônic theo tỉ số
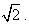
.
Ta đi đến bài toán sau : Trong mặt phẳng Oxy, cho elip (E):
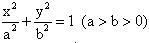
. Gọi I là trung điểm của đoạn thẳng AB nối hai đỉnh nằm trên hai trục của (E). Tia OI cắt (E) tại một điểm K. Tính tỉ số
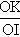
.
Ta có, toạ độ hai đỉnh của (E) là : A(a; 0) và B(0; b).
Toạ độ trung điểm I của AB là:
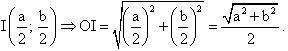
.
Phương trình của tia OI :
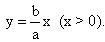
.
Toạ độ giao điểm K của tia OI và (E) là nghiệm của hệ phương trình:
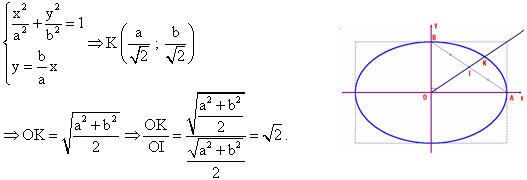
Từ đây, ta có cách dựng elip (E):
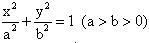
theo 5 điểm trên phần mềm tin học Cabri như sau :
Hiện hệ trục Oxy.
Dựng 4 đỉnh của (E): A(a ; 0) ; A/(-a ; 0) ; B(0 ; b) ; B/(0 ; -b).
Dựng trung điểm I của AB.
Phép vị tự tâm O tỉ số k =
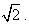
, biến điểm I thành K.
Cônic qua 5 điểm A, A/, B, B/, K chính là (E) cần dựng.
Muốn biết phương trình của (E) ta thực hiện:
kích vào (E), khi đó ta có ngay phương trình của (E).
Cách 2. Ảnh của một đuờng tròn qua phép biến đổi trực giao là một elip.
Ta chứng minh như sau :
Giả sử C là một đường tròn, D là một đường thẳng,
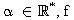
là phép co trực giao với trục D và tỉ số
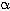
. Ta kí hiệu Ω và R là tâm và bán kính của C, và xét trong hệ quy chiếu trực chuẩn thuận
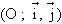
trong đó O là hình chiếu vuông góc của Ω lên D,
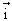
là một vector chuẩn hoá định hướng D,
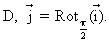
.
Trong hệ quy chiếu, Ω có toạ độ
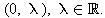
Cho M(x, y) thuộc mặt phẳng afin Euclide định hướng.
Ta có :
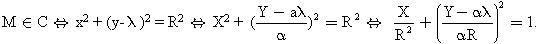
Vậy f(C) là một elip, tâm
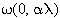
(ảnh của
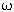
qua f), các bán trục R và |
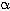
|R.
Một số khái niệm riêng biệt của chứng minh này như mặt phẳng Euclide định hướng, phép biến đổi trực giao, ... bạn đọc có thể tìm thấy trong bất cứ tài liệu hình học nào. Tôi xin không được đưa vào vì như thế thì quá dài dòng.
Nếu bạn không hiểu cách 2 này, thì tôi có thể giới thiệu một các giải giống hệt được diễn giải dễ hiểu hơn qua bài toán sau :
Bài toán Coi elip mà hai trục AOA’ = 2a, BOB’ = 2b, đường tròn chính là (O, a). Chứng tỏ rằng khi thực hiện phép
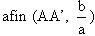
thì đường tròn chính biến thành elip.
Giải
Khi lấy một điểm M
1(x
1, y
1) ở trên vòng tròn chính thì toạ độ của nó thoả mãn hệ thức
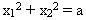
(4).Thực hiện phép
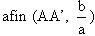
, M
1 biến thành M(x, y).
Ta có
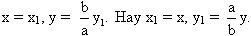
. Hệ thức (4) thành
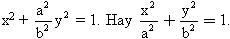
Điều này chứng tỏ M ở trên elip.
Từ cơ sở toán, bạn đọc có thể tìm ra cách dựng một cách dễ dàng. Để minh hoạ, tôi xin đưa ra cách dựng :
Hiện hệ trục Oxy.
Dựng đường tròn (O ; a) có OB = OB’ = b (b < a) ; OA =OA’ = R ; OB1 = OB'
1 = R.
Đo OB, OB
1. Dùng
đo tỉ số
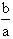
là c.
Gọi M
1 là điểm trên (O). Hạ đường vuông góc M
1H xuống AA’.
Dựng M sao cho HM = c . M
1H.
Vẽ cônic đi qua 5 điểm A’, B, M, A, B’, ta có elip cần dựng.
 Cách 3.
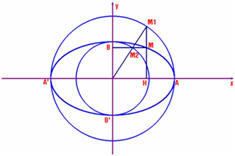
Cách 3. Tôi xin cung cấp thêm cho các bạn một cách vẽ elip như sau :
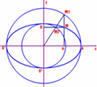
Ta vẽ hai đường tròn (O, a) và (O, b). Một nửa đường thẳng qua O cắt chúng ở M
1 M
2.
Đặt
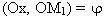
Ta có : M
1 có toạ độ :
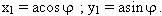
. M2 có toạ độ :
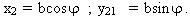
. Hạ
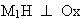
,
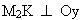
. M
1H và M
2 K cắt nhau ở M. Ta có : M có toạ độ :
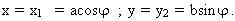
. Vậy M ở trên elip :
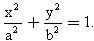
.
Từ cơ sở toán, ta có cách dựng tương ứng trên phần mềm hình học động một cách dễ dàng. Ta làm như sau :
Dựng đường tròn (O, a).
Dựng đường tròn (O, b).
Dựng nửa đường thẳng qua O cắt đường tròn tại M
1, M
2.
Hạ đường vuông góc M
1H.
Hạ qua M
2 đường vuông góc với M
1H cắt M
1H tại M.
Cônic đi qua 5 điểm A, M, B, A, B’ là elip cần dựng.
Rõ ràng, với các cách dựng khi biết cơ sở toán như trên, ta đã hiểu rõ được bản chất của phép dựng elip. Bạn có thể tìm quỹ tích, trình diễn với các hình vẽ của elip, … Các cách trình diễn này với cơ sở toán được hiểu rõ một cách căn cơ sẽ làm thoả mãn cho tất cả bất cứ ai yêu thích phần mềm hình học động. Bài viết về elip đến đây tạm dừng. Bài viết sau sẽ là cơ sở toán của hyperbol. Nội dung của nó ra sao ? Xin mời các bạn đón đọc bài 2 sẽ rõ.

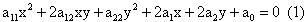
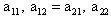 không đồng thời bằng 0.
không đồng thời bằng 0.
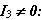 : Đường bậc hai không suy biến.
: Đường bậc hai không suy biến. 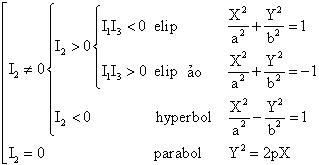

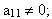 chia hai vế của (1) cho a11 ta được một phương trình có dạng như sau:
chia hai vế của (1) cho a11 ta được một phương trình có dạng như sau: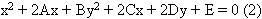
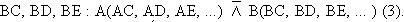 Và ánh xạ cộng tuyến này xác định một cônic không suy biến thuộc A, B, C, D, E. Cônic này là duy nhất vì (3) là duy nhất.
Và ánh xạ cộng tuyến này xác định một cônic không suy biến thuộc A, B, C, D, E. Cônic này là duy nhất vì (3) là duy nhất.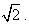 .
.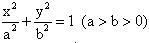 . Gọi I là trung điểm của đoạn thẳng AB nối hai đỉnh nằm trên hai trục của (E). Tia OI cắt (E) tại một điểm K. Tính tỉ số
. Gọi I là trung điểm của đoạn thẳng AB nối hai đỉnh nằm trên hai trục của (E). Tia OI cắt (E) tại một điểm K. Tính tỉ số 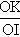 .
.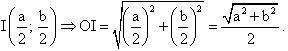 .
.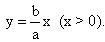 .
.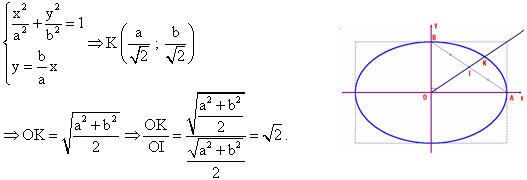
 kích vào (E), khi đó ta có ngay phương trình của (E).
kích vào (E), khi đó ta có ngay phương trình của (E).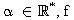 là phép co trực giao với trục D và tỉ số
là phép co trực giao với trục D và tỉ số 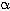 . Ta kí hiệu Ω và R là tâm và bán kính của C, và xét trong hệ quy chiếu trực chuẩn thuận
. Ta kí hiệu Ω và R là tâm và bán kính của C, và xét trong hệ quy chiếu trực chuẩn thuận 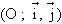 trong đó O là hình chiếu vuông góc của Ω lên D,
trong đó O là hình chiếu vuông góc của Ω lên D, 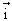 là một vector chuẩn hoá định hướng D,
là một vector chuẩn hoá định hướng D, 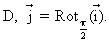 .
.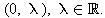 Cho M(x, y) thuộc mặt phẳng afin Euclide định hướng.
Cho M(x, y) thuộc mặt phẳng afin Euclide định hướng. 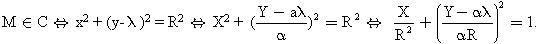
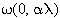 (ảnh của
(ảnh của 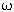 qua f), các bán trục R và |
qua f), các bán trục R và |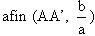 thì đường tròn chính biến thành elip.
thì đường tròn chính biến thành elip. 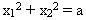 (4).Thực hiện phép
(4).Thực hiện phép 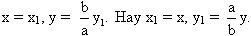 . Hệ thức (4) thành
. Hệ thức (4) thành 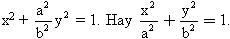
 đo tỉ số
đo tỉ số 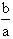 là c.
là c.
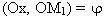 Ta có : M1 có toạ độ :
Ta có : M1 có toạ độ : 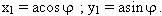 . M2 có toạ độ :
. M2 có toạ độ : 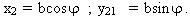 . Hạ
. Hạ 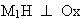 ,
, 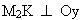 . M1H và M2 K cắt nhau ở M. Ta có : M có toạ độ :
. M1H và M2 K cắt nhau ở M. Ta có : M có toạ độ : 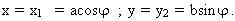 . Vậy M ở trên elip :
. Vậy M ở trên elip : 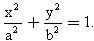 .
.

