The Algorithm:
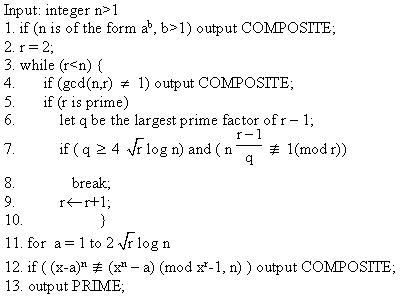
Định lý nhỏ Fermat
Nếu p là số nguyên tố và a là số nguyên tuỳ ý thì 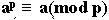
Có thể nói không quá rằng, định lý nhỏ Fermat về số nguyên tố có tầm quan trọng rất lớn không những trong toán mà còn trong tin học. Vậy một câu hỏi đặt ra là, liệu Fermat còn có những nghiên cứu về số nguyên tố nào khác nữa hay không? Và chúng có điều gì thú vị cần lưu ý?
Lúc sinh thời Fermat thường trao đổi với bạn bè về những phát hiện qua các bức thư. Chính vì thế chúng ta đã có được những trang tư liệu cực kỳ quý giá về những đóng góp của ông. Qua việc tìm hiểu những trang thư và những tư liệu liên quan người ta cho rằng, những phát hiện sau là của nhà toán học lỗi lạc này:
(1) Nếu n không là số nguyên tố thì 2n – 1 không là số nguyên tố.
(2) Nếu n là số nguyên tố thì 2n - 2 là bội của n.
Khẳng định đầu tiên có thể được chứng minh trực tiếp bằng việc phân tích 2n - 1 thành nhân tử. Vì n là hợp số, nên n = pq (Với p, 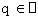 , p>1, q>1). Ta có: , p>1, q>1). Ta có:
2n-1 = 2pq – 1 = (2p(q-1) + 2p(q-2) + … + 1)
Vậy rõ ràng 2n – 1 không là số nguyên tố.
Khẳng định thứ hai chính là trường hợp riêng của định lý nhỏ Fermat mà ta đã đề cập ở trên. Xuất phát từ việc nghiên cứu định lý nhỏ Fermat, Euler đã đưa ra định lý tổng quát hơn:
Định lý Euler:
Nếu m là số nguyên dương và (a,m)=1 thì 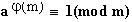
Ở đây, 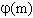 là số các số nguyên dương không vượt quá m nguyên tố cùng nhau với m. là số các số nguyên dương không vượt quá m nguyên tố cùng nhau với m.
Tuy vậy, không phải phát hiện nào của Fermat củng đúng. Ông đã từng cho rằng số có dạng 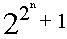 là số nguyên tố xuất phát từ việc lập bảng quan sát: là số nguyên tố xuất phát từ việc lập bảng quan sát:
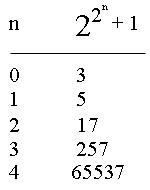
đều là số nguyên tố.
Nhưng cũng chính nhà bác học Leonhard Euler vào năm 1732 đã chứng minh được nhận định này là sai. Với trường hợp n = 5 Euler đã phân tích được 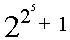 là hợp số: là hợp số:
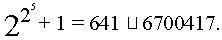
Một điều lý thú khác, đó là vào năm 1794, ở tuổi 17, Gauss đã tìm ra cách dựng đa giác đều p - cạnh, với p là số nguyên tố Fermat. Nghĩa là, chỉ bằng thước và compa ta sẽ dựng được đa giác đều 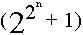 - cạnh với - cạnh với 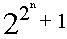 là số nguyên tố . Vì thế các đa giác đều 3-cạnh, 5-cạnh, 17-cạnh, 257-cạnh, 65537-cạnh là dựng được. Ví dụ ta có thể dựng được ngũ giác đều. Các đỉnh của ngũ giác đều nằm trên đường tròn nên ta phải giả định là đã biết trước được đường tròn ngoại tiếp của nó. Sau đây là cách dựng (Xem hình): là số nguyên tố . Vì thế các đa giác đều 3-cạnh, 5-cạnh, 17-cạnh, 257-cạnh, 65537-cạnh là dựng được. Ví dụ ta có thể dựng được ngũ giác đều. Các đỉnh của ngũ giác đều nằm trên đường tròn nên ta phải giả định là đã biết trước được đường tròn ngoại tiếp của nó. Sau đây là cách dựng (Xem hình):
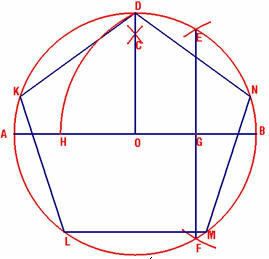 Trong một đường tròn ngoại tiếp đã biết, vẽ một đường kính bất kỳ AB. Lấy A, B làm tâm và lấy một đoạn thẳng bất kỳ lớn AO làm bán kính, vẽ hai cung gặp nhau ở C, nối OC (lúc cần thiết phải kéo dài) gặp đường tròn tại D. Lấy B làm tâm, BO làm bán kính vẽ một cung gặp đường tròn tại E và F, nối EF, gặp BO tại G. Lấy G làm tâm vẽ một cung có bán kính bằng khoảng cách DG, lấy G làm tâm vẽ cung có bán kính bằng khoảng cách DG, gặp AO tại H. Lấy D làm tâm vẽ cung có bán kính là khoảng cách DH gặp đường tròn tại K. Sau đó lấy DK làm bán kính, K làm tâm vẽ một cung cắt đường tròn O ở L, cũng làm tương tự ta được M, N. Nối DK, KL, LM, MN, ND được ngũ giác đều DKLMN. Trong một đường tròn ngoại tiếp đã biết, vẽ một đường kính bất kỳ AB. Lấy A, B làm tâm và lấy một đoạn thẳng bất kỳ lớn AO làm bán kính, vẽ hai cung gặp nhau ở C, nối OC (lúc cần thiết phải kéo dài) gặp đường tròn tại D. Lấy B làm tâm, BO làm bán kính vẽ một cung gặp đường tròn tại E và F, nối EF, gặp BO tại G. Lấy G làm tâm vẽ một cung có bán kính bằng khoảng cách DG, lấy G làm tâm vẽ cung có bán kính bằng khoảng cách DG, gặp AO tại H. Lấy D làm tâm vẽ cung có bán kính là khoảng cách DH gặp đường tròn tại K. Sau đó lấy DK làm bán kính, K làm tâm vẽ một cung cắt đường tròn O ở L, cũng làm tương tự ta được M, N. Nối DK, KL, LM, MN, ND được ngũ giác đều DKLMN.
Thêm vào đó, các đa giác đều p - cạnh với p là số nguyên tố không phải là số nguyên tố Fermat thì ta không thể dựng được. Ta sẽ minh chứng cho nhận định này bằng trường hợp p = 7. Ta biết rằng các đỉnh của hình bảy cạnh đều là các nghiệm của phương trình z7 -1 = 0, trong đó các tọa độ x, y của mỗi đỉnh là các phần thực và phần ảo của số phức z = x + iy. Một nghiệm là z = 1, các nghiệm còn lại sẽ thỏa mãn phương trình:
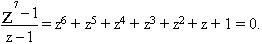
Chia cho z3 ta được phương trình mới:
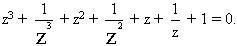
Bằng việc thực hiện các phép biến đổi đại số đơn giản ta sẽ thu được:
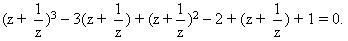
Đặt 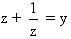 ta được phương trình bậc 3: y3 + y2 – 2 y – 1 = 0 (*). Ta biết rằng z là căn bậc bảy của đơn vị được cho bởi công thức ta được phương trình bậc 3: y3 + y2 – 2 y – 1 = 0 (*). Ta biết rằng z là căn bậc bảy của đơn vị được cho bởi công thức 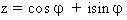 trong đó trong đó 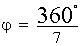 là góc nhìn từ tâm đường tròn xuống cạnh của đa giác; ngoài ra, ta còn suy ra là góc nhìn từ tâm đường tròn xuống cạnh của đa giác; ngoài ra, ta còn suy ra 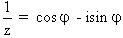 , như thế thì , như thế thì 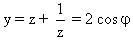 . .
Nếu ta biết cách dựng y thì ta biết dựng cả 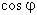 và ngược lại, Như vậy, nếu ta chứng minh được rằng không thể dựng được y thì cũng chính là chứng minh được rằng không thể dựng được cả và ngược lại, Như vậy, nếu ta chứng minh được rằng không thể dựng được y thì cũng chính là chứng minh được rằng không thể dựng được cả 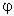 lẫn z, do đó sẽ không dựng được hình bảy cạnh. Mà để chứng minh điều này thì tương đương với việc chứng minh phương trình(*) không có nghiệm hữu tỷ. Ta sẽ chứng minh bằng phương pháp gián tiếp. Giả sử phương trình (*) có nghiệm hữu tỷ lẫn z, do đó sẽ không dựng được hình bảy cạnh. Mà để chứng minh điều này thì tương đương với việc chứng minh phương trình(*) không có nghiệm hữu tỷ. Ta sẽ chứng minh bằng phương pháp gián tiếp. Giả sử phương trình (*) có nghiệm hữu tỷ 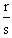 , trong đó r và s là những số nguyên không có thừa số chung. nếu như vậy thì đẳng thức r3 + r2s - 2rs2 – s3 = 0 phải được thoả mãn. Từ đó rõ ràng r3 chia hết cho s, còn s3 chia hết cho r. Bởi vì r và s là các số nguyên tố cùng nhau, cho nên mỗi số đó phải bằng , trong đó r và s là những số nguyên không có thừa số chung. nếu như vậy thì đẳng thức r3 + r2s - 2rs2 – s3 = 0 phải được thoả mãn. Từ đó rõ ràng r3 chia hết cho s, còn s3 chia hết cho r. Bởi vì r và s là các số nguyên tố cùng nhau, cho nên mỗi số đó phải bằng 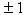 . Nghĩa là cả y (Nếu nó là số hữu tỷ) cũng phải bằng hoặc (+ 1) hoặc (-1). Nhưng phép thế vào phương trình (*) chứng tỏ cả 1, -1 đều không phải là nghiệm của phương trình. Vì thế, không thể dựng được y và do đó không thể dựng được cạnh của hình đa giác bảy cạnh đều. . Nghĩa là cả y (Nếu nó là số hữu tỷ) cũng phải bằng hoặc (+ 1) hoặc (-1). Nhưng phép thế vào phương trình (*) chứng tỏ cả 1, -1 đều không phải là nghiệm của phương trình. Vì thế, không thể dựng được y và do đó không thể dựng được cạnh của hình đa giác bảy cạnh đều.
Như vậy, tôi đã trình bày với các bạn đôi điều lý thú xoay quanh câu chuyện về những khám phá số nguyên tố của Fermat. Qua đó ta thấy rõ rằng, số nguyên tố Fermat nói riêng và số nguyên tố nói chung không chỉ xuất hiện trong số học hay tin học mà còn xuất hiện trong rất nhiều lĩnh vực khác như đại số, giải tích hay hình học. Những yếu tố đan xen giữa thực và phức, giữa tin học, số học , giải tích và hình học đã tạo ra một nét đẹp rất riêng mà số nguyên tố mang lại. Chính điều này đã góp phần tạo ra một cách nhìn đầy đủ hơn, chính xác hơn về một loại số cực kỳ quan trọng trong toán học này.
(Nguyễn Ngọc Giang-229/85 Thích Quảng Đức, Phường 4 ,Quận Phú Nhuận, Tp. Hồ Chí Minh)
School@net (Theo THNT)
|

 Có lẽ các bạn đã từng biết đến thuật toán tìm số nguyên tố nổi tiếng này. Ngay từ lúc ra đời, nó đã được mọi người thừa nhận là “một công thức thần diệu”. Sở dĩ có được điều đó là do nó cho phép xác định chính xác những số nguyên tố lên tới hàng trăm chữ số với thời gian tương đối ngắn . Thuật toán này lại bắt nguồn từ việc nghiên cứu một định lý rất đỗi quen thuộc trong toán học, định lý nhỏ Fermat
Có lẽ các bạn đã từng biết đến thuật toán tìm số nguyên tố nổi tiếng này. Ngay từ lúc ra đời, nó đã được mọi người thừa nhận là “một công thức thần diệu”. Sở dĩ có được điều đó là do nó cho phép xác định chính xác những số nguyên tố lên tới hàng trăm chữ số với thời gian tương đối ngắn . Thuật toán này lại bắt nguồn từ việc nghiên cứu một định lý rất đỗi quen thuộc trong toán học, định lý nhỏ Fermat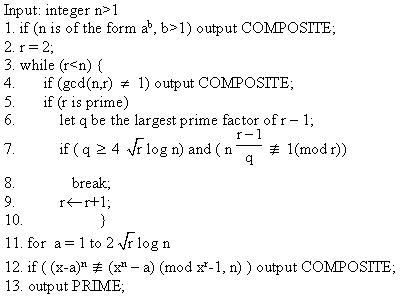
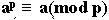
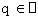 , p>1, q>1). Ta có:
, p>1, q>1). Ta có: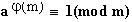
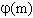 là số các số nguyên dương không vượt quá m nguyên tố cùng nhau với m.
là số các số nguyên dương không vượt quá m nguyên tố cùng nhau với m.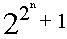 là số nguyên tố xuất phát từ việc lập bảng quan sát:
là số nguyên tố xuất phát từ việc lập bảng quan sát: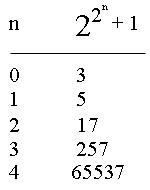
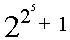 là hợp số:
là hợp số: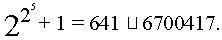
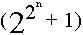 - cạnh với
- cạnh với 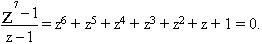
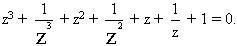
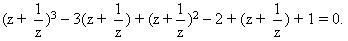
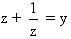 ta được phương trình bậc 3: y3 + y2 – 2 y – 1 = 0 (*). Ta biết rằng z là căn bậc bảy của đơn vị được cho bởi công thức
ta được phương trình bậc 3: y3 + y2 – 2 y – 1 = 0 (*). Ta biết rằng z là căn bậc bảy của đơn vị được cho bởi công thức 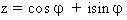 trong đó
trong đó 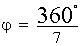 là góc nhìn từ tâm đường tròn xuống cạnh của đa giác; ngoài ra, ta còn suy ra
là góc nhìn từ tâm đường tròn xuống cạnh của đa giác; ngoài ra, ta còn suy ra 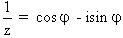 , như thế thì
, như thế thì 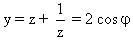 .
.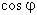 và ngược lại, Như vậy, nếu ta chứng minh được rằng không thể dựng được y thì cũng chính là chứng minh được rằng không thể dựng được cả
và ngược lại, Như vậy, nếu ta chứng minh được rằng không thể dựng được y thì cũng chính là chứng minh được rằng không thể dựng được cả 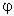 lẫn z, do đó sẽ không dựng được hình bảy cạnh. Mà để chứng minh điều này thì tương đương với việc chứng minh phương trình(*) không có nghiệm hữu tỷ. Ta sẽ chứng minh bằng phương pháp gián tiếp. Giả sử phương trình (*) có nghiệm hữu tỷ
lẫn z, do đó sẽ không dựng được hình bảy cạnh. Mà để chứng minh điều này thì tương đương với việc chứng minh phương trình(*) không có nghiệm hữu tỷ. Ta sẽ chứng minh bằng phương pháp gián tiếp. Giả sử phương trình (*) có nghiệm hữu tỷ 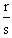 , trong đó r và s là những số nguyên không có thừa số chung. nếu như vậy thì đẳng thức r3 + r2s - 2rs2 – s3 = 0 phải được thoả mãn. Từ đó rõ ràng r3 chia hết cho s, còn s3 chia hết cho r. Bởi vì r và s là các số nguyên tố cùng nhau, cho nên mỗi số đó phải bằng
, trong đó r và s là những số nguyên không có thừa số chung. nếu như vậy thì đẳng thức r3 + r2s - 2rs2 – s3 = 0 phải được thoả mãn. Từ đó rõ ràng r3 chia hết cho s, còn s3 chia hết cho r. Bởi vì r và s là các số nguyên tố cùng nhau, cho nên mỗi số đó phải bằng 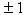 . Nghĩa là cả y (Nếu nó là số hữu tỷ) cũng phải bằng hoặc (+ 1) hoặc (-1). Nhưng phép thế vào phương trình (*) chứng tỏ cả 1, -1 đều không phải là nghiệm của phương trình. Vì thế, không thể dựng được y và do đó không thể dựng được cạnh của hình đa giác bảy cạnh đều.
. Nghĩa là cả y (Nếu nó là số hữu tỷ) cũng phải bằng hoặc (+ 1) hoặc (-1). Nhưng phép thế vào phương trình (*) chứng tỏ cả 1, -1 đều không phải là nghiệm của phương trình. Vì thế, không thể dựng được y và do đó không thể dựng được cạnh của hình đa giác bảy cạnh đều.

