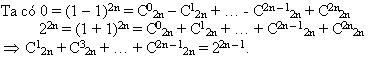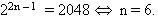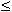Chúng ta hãy đến với bài toán sau. Bài toán 1Tìm số nguyên dương n thoả mãn hệ thức 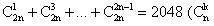 là số tổ hợp chập k của n phần tử) là số tổ hợp chập k của n phần tử) (Đề thi tuyển sinh Đại học, khối D, năm 2008) Sau đây là đáp án của bộ giáo dục : 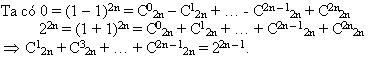
Từ giả thiết suy ra 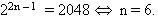 Để có thể giải được bài toán bằng phương pháp lập trình thì ta cần phân tích một số dữ kiện. Ta biết rằng, C12n+ C32n + … + C2n – 12n = 2048 thì n 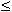 8 vì lúc đó 8 vì lúc đó Từ đây, ta có thuật toán như sau : Thuật toán 1 1. n = 0 ; 2. Trong khi (n < 8) thì 2.1. Tăng n lên 1. 2.2. s =0. 2.3. Cho i chạy từ 0 tới n - 1 2.3.1. s := s + C2i+12n. 2.4. Nếu (s == 2048) thì 2.5. Xuất ra số cần tìm là n. 3. Quay lại bước 2. 4. Kết thúc thuật toán. Từ thuật toán, ta có chương trình được viết bằng ngôn ngữ lập trình C++ : Chương trình 1 #include #include #include const k=2048 ; int TH(int m, int k); void main() {clrscr(); int n=0; double max; cout<<"CHUONG TRINH GIAI TOAN THI DAI HOC BANG PHUONG PHAP LAP TRINH" ; cout<<"
Nguoi lap trinh: Nguyen Ngoc Giang
"; cout<<"
DE TOAN:
"; cout<<"
Tim n
"; cout<<"
LOI GIAI:
"; while(n<8) {n ++ ; int s=0; for(int i=0; i s+=TH(2*n,2*i+1); if (s==k) cout<<"
so can tim la :"< } getch(); } int TH(int m, int k) {if (k<0||k>m) return 0; if(k==0 || k==m) return 1; else return TH(m-1,k-1)+TH(m-1,k); } Kết quả sau khi chạy chương trình : CHUONG TRINH GIAI TOAN THI DAI HOC BANG PHUONG PHAP LAP TRINH Nguoi lap trinh: Nguyen Ngoc Giang DE TOAN: Tim n LOI GIAI: so can tim la : 6 Cũng là điều kiện dừng C12n+ C32n + … + C2n – 12n = 2048 nhưng ta có thể viết được dưới dạng thuật toán tìm kiếm nhị phân. Ý tưởng của thuật toán được viết dưới dạng sau : Thuật toán 2 1. l = 0, mid, r = 8. 2. x = 2048. 3. Trong khi (l < r) 3.1. mid = (l + r)/2. 3.2. Nếu (x == Tong(mid)) 3.2.1. Xuất ra số cần tìm là mid. 3.3. Nếu (x > Tong(mid)) 3.4. l =mid. 3.5. Nếu (x < Tong(mid)) 3.6. r = mid. 4. Quay lại bước 3. 5. Kết thúc thuật toán. Chương trình viết bằng ngôn ngữ lập trình C++ như sau : Chương trình 2 #include #include int Tong(int m); int TH(int m, int k); void main() { clrscr(); int l = 0 , mid , r = 8 ; int x = 2048; while (l < r) { mid = (l + r) / 2 ; if (x == Tong(mid)) {cout<<"
So can tim la : " ; cout< break; } if (x > Tong(mid)) l = mid; if (x < Tong(mid)) r = mid; } getch(); } int Tong(int m) { int s = 0; for(int i = 0; i s+= TH(2*m,2*i+1); return s; } int TH(int m, int k) { if (k<0||k>m) return 0; if(k==0 || k==m) return 1; else return TH(m-1,k-1)+TH(m-1,k); } Kết quả sau khi chạy chương trình : So can tim la : 6 Bây giờ cũng là điều kiện dừng là C12n + C32n + … + C2n – 12n= 2048, nhưng được viết dưới dạng sau : Thuật toán 3 1. n = 0 ; 2. Trong khi (Tong(n) (C12n + C32n + … + C2n – 12n ) ! = 2048) thì 2.1. Tăng n lên 1. 2.2. Nếu (Tong(n) ==2048) 2.3. Xuất ra số cần tìm là n. 3. Quay lại bước 2. 4. Kết thúc thuật toán. Từ thuật toán ta có chương trình viết bằng ngôn ngữ lập trình C++ : Chương trình 3 #include #include #include const h = 2048; int TH(int m, int k); int Tong(int n); void main() {clrscr(); int n =0; double max ; cout<<"CHUONG TRINH GIAI TOAN THI DAI HOC NAM 2008 BANG PHUONG PHAP LAP TRINH" ; cout<<"
Nguoi lap trinh: Nguyen Ngoc Giang
"; cout<<"
DE TOAN:
"; cout<<"
Tim n
"; cout<<"
LOI GIAI:
"; while (Tong(n)!=h) { n++; if (Tong(n)==h) cout<<"
So can tim la : "< } getch(); } int Tong(int m) { int s = 0; for(int i = 0; i s+= TH(2*m,2*i+1); return s; } int TH(int m, int k) { if (k<0||k>m) return 0; if(k==0 || k==m) return 1; else return TH(m-1,k-1)+TH(m-1,k); } Kết quả sau khi chạy chương trình : CHUONG TRINH GIAI TOAN THI DAI HOC BANG PHUONG PHAP LAP TRINH Nguoi lap trinh: Nguyen Ngoc Giang DE TOAN: Tim n LOI GIAI: so can tim la : 6 Cần lưu ý thêm rằng với bài toán này, chúng ta hoàn toàn có thể giải nó bằng phương pháp lập trình khi đi thi. Nghĩa là chúng ta có thể lập luận bằng phương pháp lập trình kể cả lập luận cũng như kết quả. Sau đây là cách giải. #include #include #include const k=2048 ; int TH(int m, int k); void main() {clrscr(); int n=0; double max; cout<<"CHUONG TRINH GIAI TOAN THI DAI HOC BANG PHUONG PHAP LAP TRINH" ; cout<<"
Nguoi lap trinh: Nguyen Ngoc Giang
"; cout<<"
DE TOAN:
"; cout<<"
Tim n
"; cout<<"
LOI GIAI:
"; while(n<8) {n ++ ; int s=0; for(int i=0; i s+=TH(2*n,2*i+1); if (s==k) cout<<"
so can tim la :"< } getch(); } int TH(int m, int k) {if (k<0||k>m) return 0; if(k==0 || k==m) return 1; else return TH(m-1,k-1)+TH(m-1,k); } Kết quả sau khi chạy chương trình : CHUONG TRINH GIAI TOAN THI DAI HOC BANG PHUONG PHAP LAP TRINH Nguoi lap trinh: Nguyen Ngoc Giang DE TOAN: Tim n LOI GIAI: so can tim la : 6 Cái khó của khi đi thi đó là làm thế nào để tìm được kết quả để ghi vào phần chạy chương trình ? Việc lập trình trên giấy thi sẽ gặp phải trường hợp khó khăn như thế này. Tuy nhiên, ta có thể mò ra được nghiệm chỉ bằng một số phép thử. Cách làm này thể hiện tư duy tìm kiếm nhị phân trong Tin học. Ta làm như sau : Lần 1 n = 8 : C12n+ C32n + … + C2n – 12n> C516 > 2048. Lần 2 n = 4 : C12n+ C32n + … + C2n – 12n= C18 + C38+ C58 + C78 = 128 < 2048. Vậy 4 < n < 8. Lần 3 n = (4 + 8)/2 = 6 : C12n+ C32n + … + C2n – 12n = C112+ C312 + C512 + C712+ C912 + C1112 = 2.(C112+ C312 + C512) = 2.(12 + 220 + 792) = 2048. Vậy với n = 6 thì C12n+ C32n + … + C2n – 12n= 2048. Từ một bài toán ta hoàn toàn có thể giải bài toán bằng phương pháp lập trình dù là làm trên giấy hay trên máy. Một bài toán tuy đơn giản nhưng lại hết sức thú vị và bổ ích. Ẩn chứa trong nó là sự phân tích điều kiện dừng. Điều kiện dừng có thể được tạo ra nhờ việc ước lượng của chúng ta. Hoặc có thể tìm kiếm theo kiểu tuần tự hay tìm kiếm nhị phân. Trong tất cả các bài toán viết về bài toàn thi Đại học từ trước đến nay thì đây là bài toán được khai thác dưới dạng lập trình nhiều nhất. Nó thể hiện một dạng tư duy sáng tạo cực kì quan trọng mà trong Toán học chúng ta thường dùng, đó là tìm nhiều cách giải cho một bài toán. Việc chấm thi cho cách giải bằng phương pháp lập trình như thế nào ? Và có lẽ các thầy cô giáo có lẽ sẽ bắt gặp ít nhiều khó khăn trong việc chấm thi bởi để chấm thi được các bài toán này cần đòi hỏi một số hiểu biết về lập trình. Thang điểm cho nóra sao ? Cách chấm thi có nên để ý đến dạng tư duy cực kì quan trong này hay không ? Những câu hỏi này lại được tiếp tục nêu lên một lần nữa để cho chúng ta bàn và tranh cãi. Mọi góp ý xin gửi về địa chỉ : Ông Nguyễn Văn Lộc, 229/85 – Thích Quảng Đức – P.4 – Q. Phú Nhuận – TP.HCM. Điện thoại : (08) 8476771. Địa chỉ email : thaygiaogiang@yahoo.com.vn. Xin trân trọng cám ơn!
School@net (Theo THNT)
|

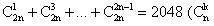 là số tổ hợp chập k của n phần tử)
là số tổ hợp chập k của n phần tử)