Mục đích của bài viết tuy nhiên không phải là giới thiệu lý thuyết về đồ thị cũng như phương pháp lập trình hướng đối tượng mà muốn trình bày một cách cài đặt đồ thị tương đối hiệu quả bằng phương pháp lập trình hướng đối tượng bằng ngôn ngữ lập trình Java. Vì vậy, tác giả xem như người đọc đã biết lý thuyết về đồ thị cũng như lập trình hướng đối tượng trên Java. I. Nhắc lại khái niệm của đồ thị Đồ thị G được cấu thành từ một tập hợp các đỉnh (Vertices) và các cạnh (Edges) ký hiệu là G = (V, E). Đồ thị G gọi là đồ thị vô hướng nếu các cạnh của G không có thứ tự, tức là chúng không phân biệt cạnh AB với BA (tương tự đường 2 chiều) Đồ thị G gọi là đồ thị vô hướng nếu các cạnh của G có thứ tự, tức là cạnh AB khác với cạnh BA (tương tự đường 1 chiều) Đồ thị có trọng số là đồ thị trong đó mỗi cạnh của đồ thị được gán bằng trọng số (khoảng cách, chi phí..v..v) II. Phân tích & Thiết kế Như thường lệ, khi bắt đầu thiết kế một chương trình hướng đối tượng chúng ta thường phải đặt ra các mục tiêu sau đây: a)Mô tả (interface) của đồ thị phải độc lập với các biến thể cài đặt chúng Vì đồ thị là một khái niệm chung chung, có rất nhiều cách đề cài đặt nó. Người này có thể cài đặt bằng phương pháp danh sách cạnh kề (Adjacency List), người kia lại thích bằng ma trận (matrix). Kiến trúc (Architecture) của chương trình chúng ta phải đảm bảo tách rời interface một đồ thị với các biến thể cài đặt chúng. b)Khả năng mở rộng (scalable) Là khả năng mở rộng chương trình mà kô phải tốn nhiều công sức thiết kế lại kiến trúc của nó. Chẳng hạn: đồ thị chúng ta sẽ cài đặt ở đây là đồ thị không trọng số,giả sử sau này ta muốn mở rộng sang loại đồ thị có trọng số thì toàn bộ kiến trúc của chương trình không được phép sụp đổ và phải thiết kế lại. Đây là một yêu cầu rất quan trọng trong lĩnh vực phát triển phần mềm vì khách hàng sau khi sử dụng phần mêm một thời gian thường có nhu cầu bổ sung các chức năng mới hoặc thay đổi một số chức năng của chương trình (change requests) c) Khả năng sử dụng lại (resuable) Đó là khi những đoạn mã chúng ta viết một lần và luôn có thể được sử dụng lại cho các ứng dụng tiếp theo. Ví dụ như: ta bỏ công ra để cài đặt đồ thị này, sau này có một lúc nào đấy ta nghiên cứu về mạng Neuron của lĩnh vực trí tuệ nhân tạo (AI). Vì mạng Neuron thực chất cũng là một đồ thị, ta có thể sử dụng lại các lớp (class) mà ta viết hôm này với khả năng kế thừa của OOP rồi thay đổi một số thuộc tính (Attribute) hoặc phương thức (Method) cho phù hợp với yêu cầu bài toán mới, ta có thể giải quyết vấn đề mới trong thời gian ngắn hơn nhiều là khi ta phải làm mọi thứ từ đầu. Đấyâu cũng là một nét đẹp của OOP vậy! Một đồ thị có nghĩa vụ cần cung cấp những giao tiếp (Methods) cơ bản sau đây: -lấy số đỉnh của đồ thị: v() -lấy số cạnh của đồ thi: e() -thêm một cạnh vào đồ thị: add(int u, int v) -xóa một cạnh khỏi đồ thị: remove(int u, int v) -kiểm tra một cạnh có thuộc đồ thị hay không: contains(int u, int v) ? -lấy ra tất cả các đỉnh kề với một đỉnh cho trước: adj(int u) -hiển thị đồ thị ra màn hình. displayGraph() Với Java ta có thể mô tả “định nghĩa” một đồ họa như trên bằng interface như sau: public interface Graph { boolean add(int u, int v); boolean remove(int u, int v); List adj(int u); boolean contains(int u, int v); int v(); int e(); void displayGraph(); } Có một điều cần lưu ý là chúng ta cần hết sức thận trọng khi thiết kế một interface!. Khi một lớp (class) cài đặt một interface thì nó phải cài đặt tất cả các phương thức của interface ấy, chẳng hạn: ta cài đặt đồ họa bằng ma trận vào gọi lớp này là : GraphMatrix. Ta sẽ có khai báo là: GraphMatrix implements Graph . Khi đấy trong phần cài đặt của lớp GraphMatrix nhất thiết phải chứa đầy đủ 7 phương thức của interface Graph từ add(int u, int v) cho đến displayGraph(). Lại giả sử rằng ta viết một thư viện cài đặt đồ thị trong đó interface Graph của chúng ta chứa 7 phương thức như ở trên . Một công ty phần mềm mua thư viện này về và khi dẫn xuất (extends) interface Graph của chúng ta họ sẽ phải cài đặt đủ 7 phương thức này. Một thời gian sau, chúng ta thấy cảm thấy không ưng ý về interface Graph ở trên và muốn thêm vào một vài phương thức mới ví dụ như: gradeSequence() đưa ra danh sách các bậc của các đỉnh của đồ thị chẳng hạn…v…v. Sau khi sửa đổi lại thư viện, công ty nọ cũng nhận được một bản cập nhật như theo thỏa thuận với interface Graph chúng ta vừa sửa đổi này. Và tại họa đã xảy ra….toàn bộ những chương trình mà công ty đã viết sử dụng interface Graph đều không họat động nữa vì các lớp cài đặt interface Graph đều không cài đặt các phuơng phức mới thêm vào interface sau này (như gradeSequence()). Bài học rút ra ở đây là: việc thiết kế interface đòi hỏi chúng ta phải nhìn trước được tất cả các phương thức mà interface cung cấp.Điều này tất nhiên là không hề đơn giản chút nào!! Quay trở lại với interface Graph. Nếu suy nghĩ kỹ ta sẽ nhận thấy một trong những thao tác quan trọng đối với một đồ thị là duyệt đồ thị theo một thứ tự nào đấy (chẳng hạn theo chiều rộng BFS, hoặc chiều sâu DFS). Với Java điều này tương đương với “Graph is iterable”. Java cung cấp interface “Iterable”, theo Java SDK Documentation: public interface Iterable {Iterator<T>iterator()
Returns an iterator over a set of elements of type T. } “Graph is iterable” chuyển thể sang ngôn ngữ Java: public interface Graph extends Iterable với khai báo này, interface Graph sẽ có thêm một phương thức mới kế thừa từ interface Iterable là Iterator<T>iterator(). Phương thức này trả về một đối tượng “Iterator”dùng để duyệt đồ thị của chúng ta. III. Các phương pháp cài đặt đồ thị Ở trên chúng ta mới chỉ mô tả “thế nào là một đồ thị” theo nghĩa một interface mà không hề đưa ra bất cứ quy định về cài đặt nào. Có rất nhiều cách đề cài đặt một đồ thị, 3 phương pháp phổ biến nhất là: a) Bằng ma trận (Matrix) Đồ thị N đỉnh được lưu trữ bởi một ma trận N x N trong đó a[u][v] = 1 nếu tồn tại cạnh giữa u và v b) Bằng danh sách kề (Adjacency list) Đồ thị N đỉnh. Một danh sách gồm N phần tử, mỗi phần tử i của danh sách này lại là một danh sách chưa các đỉnh liền kề với đỉnh i . c) Danh sách cạnh (Edges list) Một danh sách chứa tất cả các cạnh của đồ thị Dưới đây là mã nguồn chương trình cài đặt đồ thị đơn giản tức là: đồ thị vô hướng, không cho phép cạnh nối một đỉnh với chính nó, giữa một cặp đỉnh tồn tại tối đa một cạnh liên kết chúng. 
bằng ma trận: import java.util.*; public class GraphMatrix implements Graph { private int v, e; private boolean connected[][];
//Contructure public GraphMatrix(int v) { //Only allow positive number of vertices if (v > 0) { this.e = 0; this.v = v; //Connected array is automatically initialized with “false” connected = new boolean[v][v]; } }
public boolean add(int u, int v) { if (!isValidNode(u) || !isValidNode(v) || (u == v) || contains(u, v)) return false; connected[u][v] = true; connected[v][u] = true; this.e++; return true; }
public boolean remove(int u, int v) { if (!isValidNode(u) || !isValidNode(v) || (u == v) || !contains(u, v)) return false;
connected[u][v] = false; connected[v][u] = false; this.e--; return true; }
public List adj(int u) { if (!isValidNode(u)) return null;
ListadjList = new LinkedList(); for (int i = 0; i < this.v; i++) if (connected[u][i]) adjList.add(i);
//The returned adj list can not be modified from outside, important!!! return (List)Collections.unmodifiableList(adjList);
} public boolean contains(int u, int v) { if (!isValidNode(u) || !isValidNode(v)) return false; else return connected[u][v]; }
public int v() { return v; } public int e() { return e; }
public Iterator iterator() { //not implemented yet return null; }
public void printGraph() { System.out.println("****GRAPH*****"); System.out.println("Number of vertices: " + this.v); System.out.println("Number of edges: " + this.e); System.out.println("Connection - Matrix"); for (int i = 0; i < this.v; i++) { for (int j = 0; j < this.v; j++) System.out.print(connected[i][j] ? "1 " : "0 "); System.out.println(); } System.out.println("***************"); }
private boolean isValidNode(int u) { return (u >= 0) && (u <= this.v-1); } } Mảng connected dùng để lưu thông tin của đồ thị. Hai biến v, e tương ứng là số đỉnh và số cạnh. Vì chúng ta chưa đi vào nghiên cứu cách thức duyệt đồ thị, tạm thời phương thức Iterator iterator() chỉ trả về giá trị null. Chương trình chính main() dùng để test: public static void main(String[] args) { Graph g = new GraphMatrix(8); g.add(0, 1); g.add(0, 2); g.add(0, 5); g.add(0, 6); g.add(0, 7); g.add(1, 7); g.add(2, 7); g.add(3, 4);g.add(3, 5); g.add(4, 5);g.add(4, 6); g.add(4, 7); //Display graph on the console g.printGraph(); //Print the list of adjacent nodes of node 0 System.out.println(g.adj(0)); } Nếu bây giờ chúng ta quyết định cài đặt đồ thị bằng danh sách kề thay bằng ma trận như ở trên và viết một lớp mới tên là: GraphAdj . Thì trong phương thức main() ở trên ta chỉ cần thay dòng Graph g = new GraphMatrix(8) bằng Graph g = new GraphAdj(8). Phần còn lại không cần phải thay đổi gì cả. Trong lớp GraphAdj ta được tự do tổ chức chương trình theo ý muốn. Đấy là một nguyên tắc quan trọng để thiết kế những chương trình có tính linh hoạt (dynamic) cao. Như đã đề cập ở trên: “Hãy tách rời phần interface vớiphần cài đặt”. Cài đặt đồ thị bằng danh sách kề và danh sách cạnh coi như bài tập để bạn đọc nghiên cứu. Một gợi ý nhỏ là, với danh sách kề các bạn có thể dùng một mảng danh sách List[] trong đó mỗi phần tử của mảng là một danh sách liên kết. Danh sách thứ i chứa các cạnh kề với đỉnh i trong đồ thị. Nếu bạn nào cần “gợi ý rõ hơn” xin liên lạc qua email: minhquang104@yahoo.com,xin viết rõ ở phần subject (no spam please!!J). V. Phương pháp tạo ngẫu nhiên một đồ thị Đối với nhiều ứng dụng đồ thị với số đỉnh rất lớn (thậm chị hàng triệu đỉnh), việc tạo đồ thị bằng tay là không tưởng, chỉ cần sử dụng khéo léo một chút hàm sinh số ngẫu nhiên, ta hoàn toàn có thể tạo ra một đồ thị một cách ngẫu nhiên không mấy khó khăn. Phương thức sau đây tạo một đồ thị ngẫu nhiên với số đỉnh v và số cạnh e cho trước: import java.util.Random; public static Graph createRandomGraph(int v, int e) { Graph g = new GraphMatrix(v); //Random ist a class of the package “java.util” used to create random numbers Random random = new Random();
while (g.e() != e) g.add(random.nextInt(v), random.nextInt(v));
return g; } VI. Duyệt đồ thị bằng “iterator”
Chúng ta ở phần trên đã tạm thời bỏ qua phần cài đặt phương thức iterator(). Trong phần này ta sẽ cài đặt cho đồ thi một “Iterator” dùng để duyệt các đỉnh của nó. Có 2 cách để duyệt đỉnh một đồ thị là: duyệt theo chiều sâu (Depth First Search) và duyệt theo chiều rộng (Breit First Search). Ý tưởng ở đây là, ta sẽ dùng một trong 2 phương pháp duyệt trên duyệt tất cả các đỉnh của một đồ thị, các đỉnh được duyệt theo thứ tự lần lượt được lưu vào danh sách List nodeList. Java đã cài đặt sẵn cho kiểu List một Iterator nên điều duy nhất chúng ta cần làm là trả về Iterator của danh sách này. Chúng ta cài đặt phương thức iterator() cho lớp GraphMatrix ở trên: Thêm vào lớp GraphMatrix các khai báo và các phương thức sau: private List nodeList; private void depthFirst() { nodeList = new LinkedList(); TreeSet visited = new TreeSet();
for (int u = 0; u < this.v; u++) if (!visited.contains(u)) depthFirstSearch(visited, u); }
private void depthFirstSearch(Set visited, int u) { //u is visited visited.add(u); //Add this node u in the nodeList nodeList.add(u);
//For each neighbour node of u which was not visited for (int i = 0; i < this.v; i++) if ((connected[u][i]) && (!visited.contains(i))) depthFirstSearch(visited, i); } depthFirstSearch() và depthFirst() là 2 phương thức quen thuộc dùng để duyệt đồ thị theo chiều sâu. Cứ một lần một đỉnh mới được thăm, chúng ta thêm nó vào danh sách nodeList. Sau khi tất cả các đỉnh đã được thăm, danh sách nodeList chứa tất cả các đỉnh theo thứ tự duyệt theo chiều sâu. Iterator danh sách này sẽ được trả về trong phương thức iterator() của GraphMatrix như dưới đây: public Iterator iterator() { depthFirst(); return nodeList.iterator(); } Từ bây giờ mỗi lần muốn duyệt đồ thị, ta chỉ cần lấy đối tương Iterator này rồi dùng vòng cặp: hasNext() - next() Iterator graphIterator = g.iterator(); while (graphIterator.hasNext()) System.out.print(graphIterator.next() + ", "); Hoàn toàn tương tự ta có thể tạo Iterator dùng để duyệt đồ thị theo chiều rộng thay vì chiều sâu. Đôi lời về Iterator: ta thấy rằng ý tưởng của việc dùng Iterator cho việc duyệt đồ thị ở đây là tách rời cách thức duyệt đồ thị với cấu trúc bên trong của đồ thị, điều đó có nghĩa là: cách thức cài đặt và lưu trưu bên trong của đồ thị được che dấu ở bên dưới (transparent) bởi iterator, người sử dụng đồ thị của chúng ta không cần quan tâm đến điều đó mà chỉ cần dùng đối tượng Iterator. Java cài đặt ý tưởng này dựa theo “Iterator – Pattern”, bạn nào muốn tìm hiểu thêm xin ghé thăm trang web sau đây: http://sern.ucalgary.ca/courses/SENG/609.04/W98/jonesb/iterator.html VII. Các khả năng mở rộng chương trình Dựa trên kiến trúc trên các bạn có thể mở rộng và cài đặt những giải thuật trên đồ thị như: mở rộng sang đồ thị có trọng số, tô màu đồ thị, tìm đường ngắn nhất bằng Dijstra v…v. Việc mở rộng sang đồ thị trọng số có thể thực hiện đơn giản bằng cách mở rộng interface Graph ở trên: public interface WeightedGraph extends Graph { //add a new edge with its weight boolean add(int u, int v, int weight); //get the weight of the edge u-v int getWeight(int u, int v); } Điều quan trọng là luôn luôn sử dụng interface Graph thay vì các lớp dẫn xuất của nó. Chẳng hạn, nếu ta cần viết một phương thức để tìm số màu ít nhất cần tô cho một đồ thị ta nên khai báo là: public static int color(Graph g) thay vì int color(GraphMatrix g) hay int color(GraphAdj g) v…v. Khi đó ta có thể truyền tham số cho phương thức này bất kỳ đồ thị cụ thể nào: GraphAdj g1 … color (g1); hay GraphMatrix g2 … Color(g2); Có như thế ta mới khai thác hết tính linh họat của tính đa hình (Polymophy) của lập trình hướng đối tượng. Lời kết: Trên đây là một phương pháp cài đặt đồ thị bằng hướng đối tượng với ngôn ngữ Java tương đối linh họat. Kinh nghiệm cho thấy là khi bắt tay vào viết một chương trình, hay cài đặt một giải thuật bằng phương pháp lập trình hướng đối tượng, bước đầu tiên là chúng ta nên thiết kế cấu trúc của chương trình, cố gắng đạt được tiêu chí của công nghệ phần mềm (Software Enginering) như: khả năng mở rộng, khả năng tái sử dụng..v.v.. Việc lao vào gõ code mà không cân nhắc cấu trúc của chương trình tưởng chừng như tiết kiệm được thời gian thật ra phải trả một giá đắt là đến một lúc chúng ta nhận ra cấu trúc của chương trình kô còn phù hợp nữa và toàn bộ chương trình phải thiết kế lại toàn bộ. Rất mong được trao đổi với bạn đọc thêm về vấn đề này. Trần Minh Quang minhquang104@yahoo.com
School@net
|

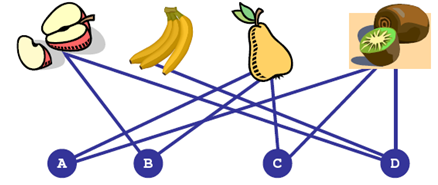
 Đồ thị (Graph) có thể nói là một trong những cấu trúc rời rạc thường được sử dụng nhất trong ngành khoa học máy tính. Mỗi khi cần mô hình hóa một tập đối tượng cùng với các mối quan hệ giữa chúng, chúng ta luôn có thể trừa tượng hóa (abstract) chúng bằng đồ thị. Một mạng giao thông, mạng máy tính, quan hệ quen biết giữa một nhóm người, quan hệ về sở thích (A thích ăn cam, B thích ăn quýt)…v…v. tất cả đều có thể đưa về mô hình của một đồ thị.
Đồ thị (Graph) có thể nói là một trong những cấu trúc rời rạc thường được sử dụng nhất trong ngành khoa học máy tính. Mỗi khi cần mô hình hóa một tập đối tượng cùng với các mối quan hệ giữa chúng, chúng ta luôn có thể trừa tượng hóa (abstract) chúng bằng đồ thị. Một mạng giao thông, mạng máy tính, quan hệ quen biết giữa một nhóm người, quan hệ về sở thích (A thích ăn cam, B thích ăn quýt)…v…v. tất cả đều có thể đưa về mô hình của một đồ thị. 



