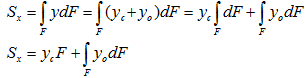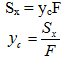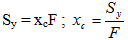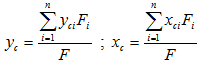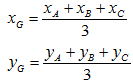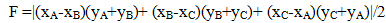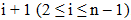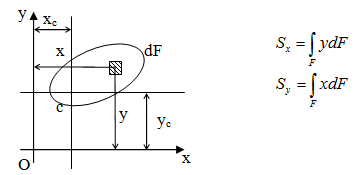
2. Trục trung tâm:Mômen tĩnh của một hình đối với một trục nào đó bằng không trục ấy gọi là trục trung tâm.

3. Trọng tâm: Giao điểm của hai trục trung tâm được gọi là trọng tâm mặt cắt.Trọng tâm là duy nhất đối với một hình phẳng.

4. Quan hệ giữa mômen tĩnh của một hình đối với một trục và khoảng cách từ trọng tâm của hình đến trục đó.

a) Giả sử có trục x bất kỳ và trục trung tâm x_c (C là trọng tâm mặt cắt) song song với trục x. Ta có y = y_c + y_o.

Thay vào công thức định nghĩa, ta được: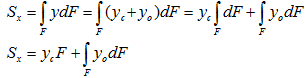

Theo định nghĩa số hạng thứ hai vế phải bằng không, do đó:

Hay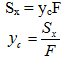

Tương tự ta tính được: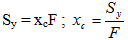

Như vậy là từ các công thức trên, ta có thể tính được mômen tĩnh của một hình nếu biết trọng tâm hoặc ngược lại xác định được trọng tâm nếu biết mômen tĩnh của hình mà không phải qua phép tính tích phân.

b) Từ đó ta có công thức tính trọng tâm hình ghép nếu biết trọng tâm của các hình thành phần.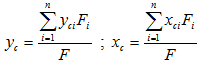

Nhận xét: Từ công thức này ta có thể tính được trọng tâm của một hình đa giác bất kỳ dựa vào các tam giác thành phần.

Công thức tính trọng tâm G, và diện tích F của hình tam giác biết toạ độ 3 đỉnh A (x_A, y_A), B (x_B, y_B) và C (x_C, y_C).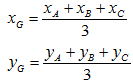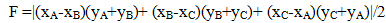

Dựa vào nhận xét trên đây tôi xin giới thiệu chương trình tính trọng tâm của một hình đa giác lồi bất kỳ.

Dữ liệu vào là n (n > 2) điểm (trong mặt phẳng Oxy) – toạ độ n đỉnh liên tiếp nhau của đa giác lồi. Ta chia đa giác lồi này thành n-2 tam giác với 3 đỉnh của tam giác lần lượt là đỉnh thứ 1, đỉnh thứ i và đỉnh thứ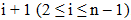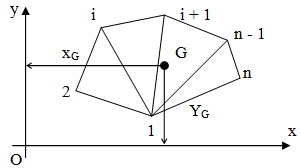

Từ đây ta có thể xây dựng chương trình, sau đây là toàn văn chương trình:

{$A+,B-,D+,E+,F-,G-,I+,L+,N-,O-,P-,Q-,R-,S+,T-,V+,X+,Y+}

{$M 16384,0,655360}

Program Xac_dinh_trong_tam ;

Const

Maxn = 1000 ;

FileInp = 'TTAM.INP' ;

FileOut = 'TTAM.Out' ;

tp = 2 ; {So chu so thap phan can}

Type

Toado = Record

x, y : Real ;

End ;

Mang = Array [1.. Maxn] of Toado ;

Var

A : Mang ;

XG, YG : Real ;

tongx, tongy, tong : Real ;

N : Integer ;

Procedure Docfile ;

Var

f : Text ;

i : Integer ;

Begin

Assign (f, FileInp) ;

{$I-}

Reset (f) ;

{$I+}

If IOResult <> 0 then Halt ;

Readln (f, N) ;

FillChar (A, Sizeof (A), 0) ;

For i := 1 to N do

Readln (f, A [i].x, A [i].y) ;

Close (f) ;

tongx := 0 ;

tongy := 0 ;

tong := 0 ;

End ;

Function XAG (AA, BB, CC : Toado) : Real ;

Begin

XAG := (AA.x + BB.x + CC.x) / 3 ;

End ;

Function YAG (AA, BB, CC : Toado) : Real ;

Begin

YAG := (AA.y + BB.y + CC.y) / 3 ;

End ;

Function SA (AA, BB, CC : Toado) : Real ;

Var

tam : Real ;

Begin

tam := (AA.x - BB.x) * (AA.y + BB.y) +

(BB.x - CC.x) * (BB.y + CC.y) +

(CC.x - AA.x) * (CC.y + AA.y) ;

SA := Abs (tam) / 2 ;

End ;

Procedure Xuly ;

Var

i : Integer ;

tamx, tamy, tamS : Real ;

Begin

For i := 2 to n - 1 do

Begin

tamx := XAG (A [1], A [i], A [i + 1]) ;

tamy := YAG (A [1], A [i], A [i + 1]) ;

tamS := SA (A [1], A [i], A [i + 1]) ;

tongx := tongx + tamx * tamS ;

tongy := tongy + tamy * tamS ;

tong := tong + tamS ;

End ;

XG := tongx / tong ;

YG := tongy / tong ;

End ;

Procedure Ghifile ;

Var

f : Text ;

Begin

Assign (f, FileOut) ;

Rewrite (f) ;

Writeln (f, XG : 0 : tp, #32, YG : 0 : tp) ;

Close (f) ;

End ;

Begin

Docfile ;

Xuly ;

Ghifile ;

End.

File vào TTAM.INP

4

0 0

4 0

4 4

0 4

File ra TTAM.OUT

2.00 2.00

Bạn đọc có thể tìm hiểu thêm để xác định được trọng tâm của một hình bất kỳ (có cả phần khuyết bên trong) đồng thời có thể xác định thêm các đặc trưng hình học khác như mô men quán tính J_x, J_y, J_xy, bán kính quán tính i_x, i_y… Rất mong sự quan tâm và trao đổi của quý bạn đọc.

Tài liệu tham khảo:

1. Sức bền vật liệu – Vũ Đình Lai (Chủ biên), Nguyễn Xuân Lựu, Bùi Đình Nghi – Nhà xuất bản giao thông vận tải Hà Nội 1997.

2. Sức bền vật liệu –Nguyễn Y Tô (Chủ biên) – Nhà xuất bản khoa học kỹ thuật Hà Nội 1996.

Địa chỉ: KS. Nguyễn Thành Quí - Phòng THƯD – Phân viện KHCN GTVT Phía Nam. Số 3 Phạm Ngọc Thạch – Phường 6 Quận 3 TPHCM.

Nguyễn Thành Quí
Email: Rotsutc@yahoo.com

School@net