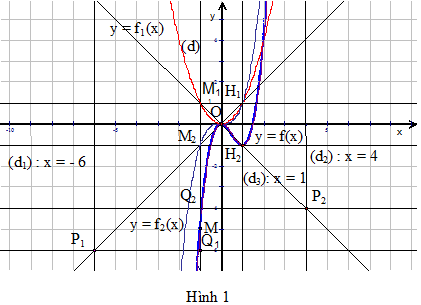
3. Cách vẽ đồ thị hàm số y = f1(x).f2(x) khi cho biết hai đồ thị hàm số y = f1(x),y = f2(x) 3.1.Bài toán III Trong mặt phẳng với hệ toạ độ Oxy cho hai đồ thị (C1): y = f1(x), (C2): y = f2(x) và hai đường thẳng (d1): x = 1, (d2) : y = x. Lấy điểm M1 trên đồ thị (C1) sao cho đườngthẳng (d)qua M1 vuông góc với x’Ox cắt đồ thị (C2) tại điểm M2. Gọi H2 là hình chiếu vuông góc của M2 lên đường thẳng (d1), đường thẳng qua M1 vuông góc với Oy cắt đường thẳng (d2) tại S, đường thẳng qua S vuông góc với x’Ox cắt đường thẳng OH2 tại H1. Gọi M là hình chiếu vuông góc của điểm H1 lên đường thẳng (d). Tìm quỹ tích các điểm M khi điểm M1 chạy trên đồ thị (C1). Lời giải Giả sử M(x; yM) với  trongđó D1 và D2 làhai tập xác định của hai hàm số trongđó D1 và D2 làhai tập xác định của hai hàm số f1(x)và f2(x), từ giả thiết ta có M1(x; f1(x)), S(f1(x); f1(x))M2(x; f2(x)), H2(1; f2(x)), H1(f1(x); yM).  Ta có: cùngphương Ta có: cùngphương
Vậy quỹ tích các điểm M là đồ thị hàm số y = f1(x).f2(x) 
3.2. Thuật toán vẽ đồ thị hàm sốy = f1(x).f2(x) khi cho biết hai đồ thị hàm sốy = f1(x), y = f2(x) B1 :Vẽ đồ thị hàm số (C1): y = f1(x), (C1): y = f2(x). B2:Vẽ hai đường thẳng (d1): x = 1, (d2): y = x. B3:Lấy điểm  , qua M1 ta vẽ đường thẳng (d)vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2. , qua M1 ta vẽ đường thẳng (d)vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2. B4 : +Dựng điểm H2 là hình chiếu vuông góc của điểm M2 lên đường thẳng (d1). +Dựng đường thẳng qua M1 vuông góc với trục Oy, lấy giao điểm S của đườngthẳng này với đường thẳng (d2). B5 :Dựng hình chiếu M của điểm H1 lên đường thẳng (d). Khi đó ta cho M1 chạy trên đồ thị (C1 ) thì điểm M vạch nên đồ thị hàm số y = f1(x).f2(x) Ví dụ 3 Từ đồ thị hai hàm số y = x2 và đồ thị y = sin(x +1) hãy vẽ đồ thị hàm số y = x2sin(x +1) bằng phần mềm hình học The Geometer’s Sketchpad. B1 :Vẽ đồ thị hàm số (C1): y = sin(x+1), (C2): y =x2. (thực hiện lệnh Graph / Plot New Fulction …) B2:Vẽ hai đường thẳng (d1): x = 1, (d2): y = x. (thực hiện lệnhPlot Points… để xác định hai điểm có toạ độ A(1;0), B(1;1); để vẽ đường thẳng (d1) ta chọn điểm A và chọn trục hoành Oxrồi thực hiện lệnh Construct / Perpendicular Line; để vẽ đường thẳng (d2)ta chọn hai điểm O, B sau đó thực hiện lệnh Construct / Line). B3:Lấy điểm  , qua M1 ta vẽ đường thẳng (d)vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2(chọn M1, chọn trục hoành Ox, thực hiện lệnh Construct / Perpendicular Line). , qua M1 ta vẽ đường thẳng (d)vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2(chọn M1, chọn trục hoành Ox, thực hiện lệnh Construct / Perpendicular Line). B4 :+Dựng điểm H2 là hình chiếu vuông góc của điểm M2 lên đường thẳng (d1) (chọn M2, chọn đường thẳng (d1), thực hiện lệnh Construct / Perpendicular Line). +Dựng đường thẳng qua điểm M1vuông góc với trục Oy, lấy giao điểm S của đường thẳng này với đường thẳng (d2) (chọn M1, chọn trục tung Oy, thực hiện lệnh Construct / Perpendicular Line). B5 :Dựng hình chiếu M của điểm H1 lên đường thẳng (d) (chọn M, chọn đường thẳng (d), thực hiện lệnh Construct / Perpendicular Line). B6:Chọn điểm M, tạo vết chọn màu (Thực hiện lệnh Display / Trace Point / Color) B7 :Chọn điểm M1, thực hiện lệnh Display / Animate Point thì điểm M đã được tô màu vạch nên đồ thị (C’’’): y = x2sin(x + 1) ( xem hình 3). Nhân tiện tôi xin giới thiệu bạn đọc một ứng dụng của bài toán III để tạo ra bài toán quỹ tích hình học phẳng; thông qua hình vẽ các bạn sẽ thấy được tính nghệ thuật của việc vẽ “đường con bướm” (tác giả tự đặt tên) trong mặt phẳng phần mềm hình học The Geometer’s Sketchpad thông qua bài toán quỹ tích hình học phẳng tương ứng. Sau đây là bài toán con bướm và hình vẽ 12 con bướm Bài toán con bướm Cho đường tròn (C) tâm I có bán kính bằngr và đường thẳng (a) sao cho đường thẳng (a) cắt đường tròn (C) tại hai điểm phân biệt và Ikhông nằm trên đường thẳng (a). Lấy điểm M0 nào đó nằm trên đường tròn (C) qua M0 vẽ đường thẳng (d)cùngphương với đường thẳng (a). Qua M0 vẽ đường thẳng vuông góc với (a) tại H0, đườngthẳng IH0 cắt đườngthẳng (d)tại M1. Qua M1vẽ đường thẳng vuông góc với (a) tại H1, đườngthẳng IH1 cắt đường thẳng (d) tại M2. Cứ như thế…,qua Mn-1vẽ đường thẳng vuông góc với (a) tại Hn-1, đường thẳng IHn–1 cắt đường thẳng (d) tại Mn. Tìm quỹ tích các điểm Mn khi M0chạy khắp đường tròn (C). Hình vẽ 16 là 12 con bướm ứng với bán kính r = 2,01, tâm I1(0; 0), I1(4,02; 0),I2 (-4,02; 0), bậc n = 0; 1; 2; 3, đường sinh (a): x = 1  4.Cách vẽ đồ thị hàm số  khi cho biết hai đồ thị hàm số y = f1(x), y = f2(x) khi cho biết hai đồ thị hàm số y = f1(x), y = f2(x) 4.1.Bài toán IV Trong mặt phẳng với hệ toạ độ Oxychohai đồthị (C1):y = f1(x), (C2):y = f2(x)và hai đườngthẳng(d1): x = 1, (d2): y = x. Lấyđiểm M1 trênđồthị (C1)saochođườngthẳng (d)qua M1 vuông góc với x’Ox cắtđồ thị (C2) tại điểm M2. QuaM1kẻđường thẳng vuông góc vớiOy cắt (d2)tạiH1. ĐườngthẳngquaM2 vuônggócvớiOycắtđườngthẳngquaH1vuônggóc vớiOx tạiH2. ĐườngthẳngOH2 cắt đường thẳng (d1) tại K. Gọi M là hình chiếu vuông góc của điểm K lên đường thẳng (d). Tìm quỹ tích các điểm M khi M1 chạy trên đồ thị (C1). Lời giải Giả sử M(x; yM) với  trongđó D1 và D2 làhai tập xác định của hai hàm sốf1(x)và f2(x), từ giả thiết ta có M1(x; f1(x)), S(f1(x); f1(x)) M2(x; f2(x)), H2(f1(x); f2(x)), H1(f1(x); f1(x)), K(1; yM), vì đường thẳng OH2 cắt đường thẳng (d1) tại K nên trongđó D1 và D2 làhai tập xác định của hai hàm sốf1(x)và f2(x), từ giả thiết ta có M1(x; f1(x)), S(f1(x); f1(x)) M2(x; f2(x)), H2(f1(x); f2(x)), H1(f1(x); f1(x)), K(1; yM), vì đường thẳng OH2 cắt đường thẳng (d1) tại K nên  cùngphương và cùngphương và  

4.2. Thuật toán vẽ đồ thị hàm số  khi cho biết hai đồ thị hàm số y = f1(x), y = f2(x) khi cho biết hai đồ thị hàm số y = f1(x), y = f2(x) B1 :Vẽ đồ thị hàm số (C1): y = f1(x), (C1): y = f2(x). B2:Vẽ hai đường thẳng (d1): x = 1, (d2): y = x. B3:Lấy điểm  , qua M1 ta vẽ đường thẳng (d)vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2. , qua M1 ta vẽ đường thẳng (d)vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2. B4 :+Dựng đường thẳng qua M1 vuông góc với trục Oy, lấy giao điểm H1 của đườngthẳng này với đường thẳng (d2). +Dựng đường thẳng qua M2vuông gócvớiOycắtđườngthẳngquaH1 vuônggóc vớiOx tạiH2. + Xác định giao điểm K của đườngthẳngOH2và đường thẳng (d1). B5 :Dựng hình chiếu M của điểm K lên đường thẳng (d). Khi đó ta cho M1 chạy trên đồ thị (C1 ) thì điểm M vạch nên đồ thị hàm số  Ví dụ 3
Từ haihàm số  hãy vẽ đồ thị hàm số bằng phần mềm hình học The Geometer’s Sketchpad. hãy vẽ đồ thị hàm số bằng phần mềm hình học The Geometer’s Sketchpad. B1 :Vẽ đồ thị hai hàm số  (thực hiện lệnh Graph / Plot New Fulction …) (thực hiện lệnh Graph / Plot New Fulction …) B2:Vẽ hai đường thẳng (d1): x = 1, (d2): y = x. (thực hiện lệnhPlot Points… để xác định hai điểm có toạ độ A(1;0), B(1;1); để vẽ đường thẳng (d1) ta chọn điểm A và chọn trục hoành Oxrồi thực hiện lệnh Construct / Perpendicular Line; để vẽ đường thẳng (d2)ta chọn hai điểm O, B sau đó thực hiện lệnh Construct / Line). B3:Lấy điểm  , qua M1 ta vẽ đường thẳng (d)vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2(chọn M1, chọn trục hoành Ox, thực hiện lệnh Construct / Perpendicular Line). , qua M1 ta vẽ đường thẳng (d)vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2(chọn M1, chọn trục hoành Ox, thực hiện lệnh Construct / Perpendicular Line). B4 : +Dựng đường thẳng qua M1 vuông góc với trục Oy, lấy giao điểm H1 của đườngthẳng này với đường thẳng (d2) (chọn M1, chọn trục tung Oy, thực hiện lệnh Construct / Perpendicular Line). +Dựng đườngthẳngquaM2 vuônggócvớiOycắtđườngthẳngquaH1vuônggóc vớiOx tạiH2 (chọn M2, chọn trục tung Oy, thực hiện lệnh Construct / Perpendicular Line; chọn H1, chọn trục hoành Ox, thực hiện lệnh Construct / Perpendicular Line). + Xác định giao điểm K của đường thẳng OH2 và đường thẳng (d1)(chọn hai điểm O và H2thực hiện lệnh Construct / Line). B5 :Dựng hình chiếu M của điểm K lên đường thẳng (d) (chọn M, chọn đường thẳng (d), thực hiện lệnh Construct / Perpendicular Line). B6:Chọn điểm M, tạo vết chọn màu (thực hiện lệnh Display / Trace Point / Color) B7 :Chọn điểm M1, thực hiện lệnh Display / Animate Point thì điểm M đã được tô màu vạch nên đồ thị (C’’’’):  ( xem hình 5). ( xem hình 5). Từ bốn bài toán quỹ tích tổng quát nói trên, ta có thể nói rằng: chỉ bằng thước thẳng có vạch chia đơn vị và thước vuông góc ta dựng được các điểm thuộc các đồ thị hàm số có dạngy = k1.f1(x) + k2.f2(x)(k1, k2 là hai số thực khác không),  khi chotrước các đồ thị hàm sốy = f1(x),y = f2(x), y = f(x). Một phép dựng đồ thị hàm số như thế này theo ý chủ quan của tác giả là mới mẻ. khi chotrước các đồ thị hàm sốy = f1(x),y = f2(x), y = f(x). Một phép dựng đồ thị hàm số như thế này theo ý chủ quan của tác giả là mới mẻ. Trong phần mềm hình học The Geometer’s Sketchpad hiện nay, theo tôi nghĩ cần viết bổ sung thêm cách vẽ đồ thị hàm số có dạng như y = k1.f1(x) + k2.f2(x)(k1, k2 là hai số thực khác không),  khi vẽ được các đồ thị hàm số y = f1(x),y = f2(x), y = f(x) thì phần mềm này sẽ phong phú và có tính ứng dụng rộng, đa dạng hơn trong việc vẽ đồ thị hàm số. Tác giả mong muốn sự hợp tác nghiên cứu của các nhà chuyên môn về vấn đề này. khi vẽ được các đồ thị hàm số y = f1(x),y = f2(x), y = f(x) thì phần mềm này sẽ phong phú và có tính ứng dụng rộng, đa dạng hơn trong việc vẽ đồ thị hàm số. Tác giả mong muốn sự hợp tác nghiên cứu của các nhà chuyên môn về vấn đề này. Tôn Thất Hiệp, giáo viên trường THPT Phan Đăng Lưu, Phú Vang, Thừa Thiên-Huế
School@net
|

 Ta biết rằng từ đồ thị hàm số (C): y = f(x) ta có thể vẽ đồ thị hàm số (C1): y = f(|x|), (C2): y =|f(x)|, (C3): y = -f(x), (C4):y = f(-x), (C5): y = f -1(x) (nếu hàm số f có hàm số ngược trên khoảng xác định của nó), (C6): y = - f(-x), (C7): y = f(x + a), (C8): y = f(x) + b, bằng các phép đối xứng trục, phép đối xứng tâm, phép tịnh tiến phù hợp.
Ta biết rằng từ đồ thị hàm số (C): y = f(x) ta có thể vẽ đồ thị hàm số (C1): y = f(|x|), (C2): y =|f(x)|, (C3): y = -f(x), (C4):y = f(-x), (C5): y = f -1(x) (nếu hàm số f có hàm số ngược trên khoảng xác định của nó), (C6): y = - f(-x), (C7): y = f(x + a), (C8): y = f(x) + b, bằng các phép đối xứng trục, phép đối xứng tâm, phép tịnh tiến phù hợp. 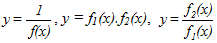 hay không ? và cách vẽ như thế nào ?. Câu trả lời là được. Bài viết này sẽ giải quyết trọn vẹn vấn đề đó.
hay không ? và cách vẽ như thế nào ?. Câu trả lời là được. Bài viết này sẽ giải quyết trọn vẹn vấn đề đó. trongđó D1 và D2 làhai tập xác định của hai hàm số
trongđó D1 và D2 làhai tập xác định của hai hàm số Ta có: cùngphương
Ta có: cùngphương 
 , qua M1 ta vẽ đường thẳng (d)vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2.
, qua M1 ta vẽ đường thẳng (d)vuông góc với trục hoành Ox sao cho đường thẳng (d) cắt (C2) tại M2. 
 khi cho biết hai đồ thị hàm số y = f1(x), y = f2(x)
khi cho biết hai đồ thị hàm số y = f1(x), y = f2(x) cùngphương và
cùngphương và 


 hãy vẽ đồ thị hàm số bằng phần mềm hình học The Geometer’s Sketchpad.
hãy vẽ đồ thị hàm số bằng phần mềm hình học The Geometer’s Sketchpad. (thực hiện lệnh Graph / Plot New Fulction …)
(thực hiện lệnh Graph / Plot New Fulction …)  ( xem hình 5).
( xem hình 5). khi chotrước các đồ thị hàm sốy = f1(x),y = f2(x), y = f(x). Một phép dựng đồ thị hàm số như thế này theo ý chủ quan của tác giả là mới mẻ.
khi chotrước các đồ thị hàm sốy = f1(x),y = f2(x), y = f(x). Một phép dựng đồ thị hàm số như thế này theo ý chủ quan của tác giả là mới mẻ.

