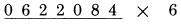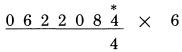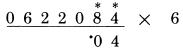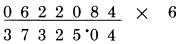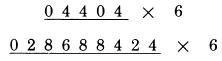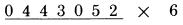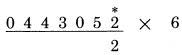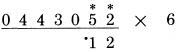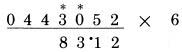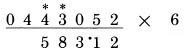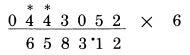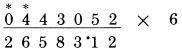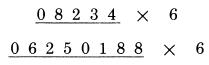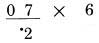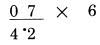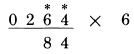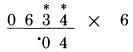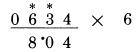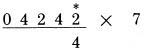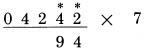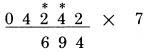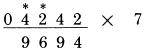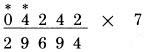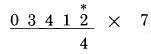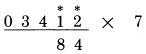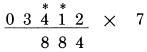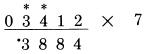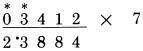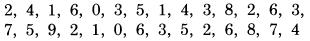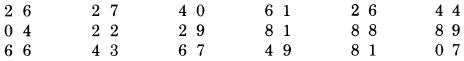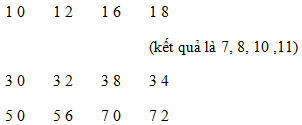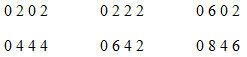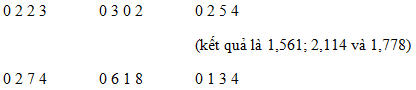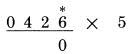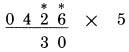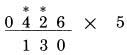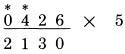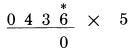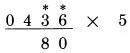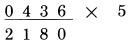Các bước được thực hiện một cách tức thời. Chúng ta không nói đến việc quan tâm đến “một nửa” của 4, mà chúng ta sẽ nhìn số 4, để nhận được số 2. Thực hiện như vậy với các chữ số còn lại: 2,6,4,5,8,7,2,9,4,3,0,7,6,8,5,8,3,6,1 Những chữ số lẻ: 1, 3, 5, 7, 9 tạo phần dư trong phép chia và cần xử lý đặc biệt. Các chữ số còn lại, đưa ra kết quả trực tiếp. THỰC HIỆN PHÉP NHÂN VỚI 6 Bây giờ ta sẽ thực hiện phép nhân bằng việc “chia đôi”. Một phần của quy tắc nhân một số với 6 là: Cộng mỗi chữ số với một nửa của số liền kề nó. Chúng ta sẽ giả thiết rằng: tạm thời chúng ta sử dụng quy tắc này là đủ để thực hiện phép nhân với 6, và thực hiện phép tính: 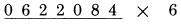
Bước 1: 4 là chữ số đầu tiên bên phải của số bị nhân, và nó không có số liền kề bên phải nên không cần thực hiện phép cộng. 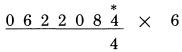
Bước 2: Chữ số thứ 2 là 8, và số liền kề với nó là 4, do vậy chúng ta cộng 8 với một nửa của 4(2), ta nhận được 10.
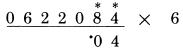
Bước 3: Số tiếp theo là 0. Ta cộng nó với một nửa của 8, là số liền kề. 0 cộng với 4 là 4, và thêm số nhớ là 1.

Lặp lại bước này với các chữ số 2, 2, 6 và 0, ta được: 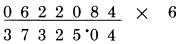 Bạn có thể thấy việc thực hiện dễ dàng của cách tính này. Thử với 2 phép nhân tiếp theo. 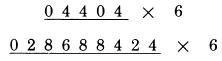
Kết quả của phép tính thứ nhất là 26,424. Kết quả của phép tính thứ 2 là 172,130,544. Chúng ta đã thực hiện xong các phép tính. Tuy nhiên đó không phải là quy tắc đầy đủ để thực hiện nhân với 6. Quy tắc đầy đủ là: Với mỗi chữ số, cộng nó với “một nửa” số bên cạnh, cộng 5 nếu đó là chữ số lẻ. Nếu chữ số đó là lẻ ta cần cộng thêm 5, nó không tạo sự khác biệt khi tính với số bên cạnh có là chữ số lẻ hay không. Chúng ta sẽ xem xét tất cả các chữ số, và kiểm tra xem nó là số chẵn hoặc số lẻ. Nếu nó là số chẵn, chúng ta chỉ đơn giản cộng nó với một nửa số liền kề. Nếu nó là lẻ, chúng ta cộng nó với 5 và sau đó cộng với một nửa số liền kề, như chúng ta đã làm ở trên. Lấy ví dụ: 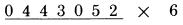
Ở các chữ số 3 và 5, là các số lẻ. Chúng ta sẽ cần phải cộng chúng với 5, thực hiện như bên dưới: Bước 1: 2 là số chẵn và là chữ số cuối, viết nó xuống 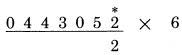
Bước 2: 5 là số lẻ, 5 cộng 5, cộng một nửa của 2, được 11 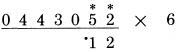
Bước 3: 5 là số lẻ, 5 cộng 5, cộng một nửa của 2, được 11 
Bước 4: 3 là số lẻ, 3 cộng 5 là lẻ 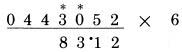
Bước 5: 4 cộng một nửa của 3 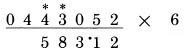
Bước 6: 4 cộng một nửa của 4 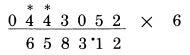
Bước cuối: 0 cộng một nửa của 4 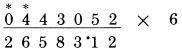
Kết quả là 2.658,312. Tất nhiên, mọi giải thích ở đây chỉ dùng để mục đích làm rõ nhất cách thức thực hiện trong lần đầu. Trong thực hành, việc thực hiện sẽ diễn ra nhanh bởi việc cộng một chữ số với một nửa chữ số liền kề là đơn giản. Với điều lưu ý duy nhất số lượng thực hiện các phép tính, việc thực hiện nó trở nên tự động. Bạn sẽ hiểu rõ ràng hơn, nếu bạn thực hiên các bước đối với các phép tính đặt ra: 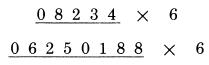
Đáp án đầu tiên là 49,404. Kết quả phép tính thứ 2 là 37,501,128. Các phép tính mà ta đã thực hiện đều với số bị nhân là số có nhiều chữ số. Ta vẫn có thể áp dụng đối với việc nhân với số có một chữ số. Thực hiên 8 nhân 6, với phương pháp trên: 
Khi số bị nhân là số lẻ, ví dụ 7, chúng ta cộng 5 vào bước đầu tiên. Tất nhiên ta không cần cộng ở bước tiếp theo, với 0 là một số chẵn. 7 cộng 5, ở hàng cuối 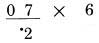
0 cộng một nửa của 7, cộng nhớ 1 là 4 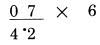
Phần lớn mọi người, có thể cảm thấy rằng, họ đã thuộc lòng bảng nhân 6. Hơn một nửa những người bình thường, có thể cảm thấy tự tin với nó để áp dụng phép nhân trong các trường hợp phức tạp hơn. Đó không phải là vấn đề ở đây. Kỹ thuật được trình bày ở trên được sử dụng lặp lại trong các phép tính phức tạp hơn, và họ sẽ cần phải dựa bảo bảng nhớ trên. Cách tốt nhất để thực hiện theo một cách thức mới đó là áp dụng nó một cách tương đối giống với cách truyền thống. Đó là cách chúng ta đang làm. Mặc dù (và đó là điều quan trọng hơn ý nghĩa của nó), đó là bắt đầu thay đổi thói quen tính toán trong đầu óc. Chúng ta đã biết tất cả về các bàn cãi về cách đọc ở những người bình thường, và các phương pháp đã được áp dụng để phát triển khả năng đọc nhanh. Có một ý kiến rằng có nhiều người có thói quen đọc từng chữ một, phát âm bất cứ từ nào họ đọc được. Chúng ta bị thúc đẩy việc phát triển thói quen đọc bằng cách nhận dạng toàn bộ chữ hoặc cụm từ tại một thời điểm. Các vấn đề khác cũng được đem lại. Đó là tất cả vấn đề: Mọi người đọc dở là kết quả của sự thói quen không hiệu quả khi đọc của họ. Điều tương tự cũng xảy ra với số học. Một người đã thất bại trọng việc áp dụng thói quen không tốt khi họ tính toán số học, và kết quả anh ta đã lãng phí thời gian và công sức. Chỉ những người, như những kế toán, những người trải qua phần lớn thời gian để làm việc với các con số, thậm chí tạo thành một thói quen trong công việc. Phần còn lại, thậm chí mặc dù chúng ta có thể không cần những việc tính toán trong công việc hàng hàng, chúng ta vẫn có thể học những phương pháp này với một chút thực hành và rèn luyện, như sẽ nói ở phần sau. Một trong những bước tính nhẩm đơn giản nhất, đã nói ở phần trước, đó là tính giá trị chia đôi của một số liền kề. Chúng ta đã thực hiện một số thực hành với một số chữ số, như 2 và 8, và đọc kết quả thành 1 và 4, mà không cần phải thực hiện các bước nhỏ trung gian nào. Kết quả sẽ hiện ngay trong đầu chúng ta ngay sau khi ta thấy chữ số 2 và 8, và bây giờ nó trở thành một phản xạ trực tiếp. Bạn có thể quay lại phần trên để xem chi tiết. Một cách rèn luyện tính nhẩm khác là đọc với chính mình chỉ kết quả của phép cộng với số liền kề, hoặc với một nửa của nó, giống như: 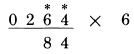
Số 8 là kết quả của 6, cộng với một nửa của 4. Nhưng ta không đọc kiểu: “một nửa của 4 là 2, cộng với 6 là 8”. Thay vì vậy, chúng ta nhìn vào số 6 và 4, nhìn thấy một nửa của 4 là 2, và đọc thành “6, 8”. Lần đầu tiên bạn sẽ cảm thấy khó khăn, vậy nên bạn có thể cải thiện bằng cách đọc “6,2,8”. Một điểm khác cần thực hành là bước cộng thêm 5 vào chữ số khi nó là số lẻ (không phải số liền kề). Hãy xem trường hợp này: 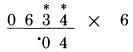
Số 0 là hàng đơn vị của 10, với dấu (.) ở trên, và 10 là kết quả của 3 cộng 5 (3 là số lẻ), và cộng thêm với 2 (là một nửa của 4). Cách làm chính xác là, đầu tiên là đọc “5,8,2,10”. Sau vài lần thực hành theo cách này, bạn có thể rút gọn lại thành “8, 10”.. Số 5 được tính đến vì 3 là số lẻ cần được cộng trước tiên, nếu không ta có thể bỏ qua nó. Theo cách tương tự, khi có một dấu chấm (.) để biểu diễn cho nhớ 1, nó cần được cộng trước khi ta cộng với số liền kề (phép nhân 11), hoặc một nửa của số liền kề (phép nhân với 6). Nếu chúng ta để lại số nhớ 1 cho đến khi chúng ta cộng với số liền kề, có thể chúng ta sẽ quên nó. Ở ví dụ sau, các chữ số được sắp xếp gọn lại theo cách: 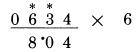
Chúng ta nhìn vị trí số 6, đọc “7”, sau khi tính với dấu (.), sau đó chúng ta đọc “8”, sau khi cộng với một nửa của 3. Lần đầu tốt nhất chúng ta nhìn vào vị trí số 6 và đọc “7”(nhớ), sau đó đọc “1” cho một nửa của 3, sau đó đọc “8”, và chúng ta viết 8. Khi chúng ta có nhớ 1 và đồng thời phải cộng thêm 5 (với số lẻ), đọc “6” thay vì “5”, sau đó cộng với chữ số đang xét. Nó sẽ cắt giảm một bước, và dễ dàng tạo thành thói quen. Lấy một cái bút chì và thử làm lại với các phép tính sử dụng duy nhất một bước tính nhẩm, như bạn đã thấy ở trên, đáp án ở phía sau: Phép nhân với 7 (cộng với số liền kề)
 Phép nhân với 12 (gấp đôi rồi cộng với số liền kề) 
Phép nhân với 6 (cộng 5, nếu nó lẻ, và cộng với một nửa số liền kề) 
Kết quả là:
 THỰC HIỆN PHÉP NHÂN VỚI 7: Quy tắc thực hiện phép nhân 7 rất giống cách thực hiện phép nhân với 6. Gấp đôi chữ số rồi cộng nó với một nửa chữ số liền kề, cộng thêm 5 nếu nó là số lẻ Giả sử chúng ta muốn thực hiện phép nhân 4,242 với 7. Do số bị nhân không có chữ số lẻ nào, do đó ta không cần thiết phải cộng thêm 5. Trong ví dụ này, ta thực hiện các bước giống như đã làm với phép nhân 6, ngoại trừ phải gấp đôi các chữ số. Bước 1: gấp đôi hàng đơn vị 2 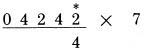
Bước 2: gấp đôi 4 và cộng một nửa số liền kề 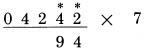
Bước 3: gấp đôi 2 và cộng một nửa số liền kề 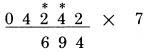
Bước 4: gấp đôi 4 và cộng một nửa số liền kề 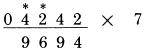
Bước cuối: gấp đôi 0, được 0 và cộng một nửa số liền kề 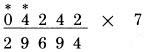
Sau đây là một ví dụ với số bị nhân có chứa chữ số lẻ. Cả 3 và 1 đều là các số lẻ: Bước 1: gấp đôi hàng đơn vị 2 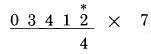
Bước 2: gấp đôi 1, cộng với 5 (vì 1 là số lẻ) được 7, và cộng thêm nửa của 2 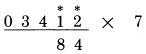
Bước 3: không có số lẻ: gấp đôi 4 và cộng một nửa của 1 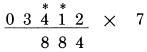
Bước 4: 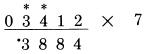
Bước cuối: gấp đôi 0, được 0, nhưng cộng một nửa của 3, cộng thêm số nhớ 1 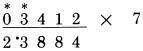
Các bước tính nhẩm trong đầu như sau: - Đánh dấu 1 bởi dấu (.), nếu phép tính có nhớ 1.
- Xem hàng sẽ làm việc tiếp theo và quan sát nó có phải là số lẻ. Nếu có, cộng 5 vào phần nhớ 1, được 6 hoặc chỉ là 5 nếu không có dấu chấm (.)
- Quan sát hàng hiện thời, gấp đôi nó. Ta tính nhẩm tổng 5 và giá trị gấp đôi này. Nếu hàng hiện thời là 3, ta được 5, và sau đó được 11 là tổng của 5 và giá trị gấp đôi của 3 trong một bước tính.
- Quan sát hàng tiếp theo, ví dụ là số 6. Chúng ta cộng một nửa giá trị của nó vào giá trị ta đang tính. Được 14
Chúng ta hãy thực hiện các bước này trong một thời gian ngắn. Việc này rất cần thiết để rèn luyện khả năng tính nhẩm, vì nò phát triển khả năng tập trung, mà khả năng tập trung là toàn bộ bí mật của thành công của phương pháp này. Việc này không thể thực hiện ngay một lúc, tuy nhiên chúng ta có thể tự cải thiện bằng cách chia thành một số pha như sau: Đầu tiên: Quan sát toàn bộ các chữ số sau và làm trực tiếp, không ngắt quãng, đọc nhẩm giá trị gấp đôi của số đó (quan sát số 3, đọc thành 6 chứ không cần đọc qua 3). 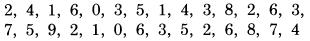
Bước 2:Với mỗi cặp số sau, nhìn vào chữ số bên trái và đọc nhẩm giá trị gấp đôi của nó (nhìn vào số 3, đọc nhẩm số 6) và cộng với số bên cạnh nó (ví dụ với cặp (3,4) chúng ta đọc thành “6 10”). Đó là một cách làm nhanh chóng để thực hiện phép nhân với 12. 
Bước 3:Với mỗi cặp số sau, nhìn vào chữ số bên trái và đọc nhẩm giá trị gấp đôi của nó, sau đó cộng nó với một nửa của số bên cạnh (nhìn 2 6, đọc thành “4 7”). Đó là cách tính nhanh trong phép nhân với 7 với các chữ số chẵn. 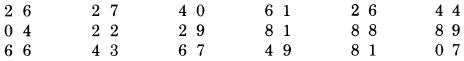
Bước 4:Với mỗi số sau, nhìn vào từng số, sau đó đọc 5 và đọc giá trị của 5 cộng với gấp đôi giá trị của chúng (nhìn vào 3, đọc “5 11”). 7, 5, 3, 1, 9, 3, 7, 5, 1 Bây giờ bạn hãy lặp lại lần nữa.
Bước 5:Với các cặp số sau, nhìn vào chữ số bên trái, đọc “5”, sau đó đọc giá trị tổng của 5 và gấp đôi giá trị vừa rồi, sau đó lập tức cộng nó với một nửa giá trị số liền kề, đọc kết quả này (ví dụ với 3,4 đọc “5 11 13”). Đó là phép nhân 7 đối với các chữ số lẻ. 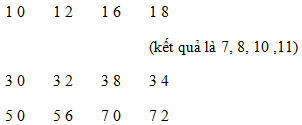
Bây giờ hãy xem bạn có thể thực hiên phép nhân với 7 nhanh như thế nào. Đầu tiên hãy thử với những số sau, đều là các số chẵn và bạn không cần thiết phải cộng với 5, bạn chỉ cần gấp đôi giá trị số bên trái và cộng nó với mộtnửa của số liền cạnh. 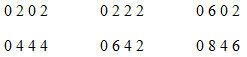 Sau đó ta kết thúc với các số có chữ số lẻ, phải cộng thêm 5 vào kết quả 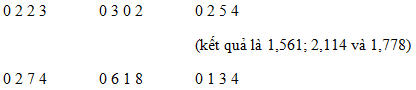
THỰC HIỆN PHÉP NHÂN VỚI 5: Quy tắc thực hiện phép nhân với 5 cũng tương tự như thực hiện phép nhân với 6 hoặc 7 nhưng đơn giản hơn. Thay vì phải cộng vào từng chữ số như chúng ta đã thực hiện phép 6, hoặc gấp đôi nó rồi cộng như đã làm với 7, chúng ta chỉ cần nhìn vào chính số đó. Quan sát xem nó là số chẵn hay số lẻ. Nếu là số lẻ, ta cộng thêm 5 như trước. Đối với mỗi chữ số, chia đôi số liền kề, sau đó cộng với 5 nếu chữ số đó lẻ. Giả sử chúng ta muốn nhân 426 với 5. số 6 là một số chẵn, không có số liền kề; không cộng thêm với 5; 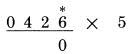
số 2 là một số chắn, lấy một nửa của 6 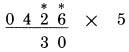
số 4 là một số chắn, lấy một nửa của 2 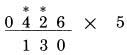
số 0 là một số chắn, lấy một nửa của 4 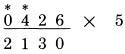
Bây giờ nếu chúng ta có một chữ số lẻ trong số bị nhân, ta cộng nó với 5. giống như ở trên 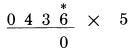
số 3 là một số lẻ, lấy 5 cộng với 3 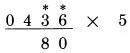
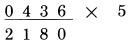
Rất dễ dàng để thực hiện. Có một số điều ta cần làm rõ. Chúng ta quan tâm đến các chữ số lẻ trước, bởi vì có một chút lưu ý khi ta làm việc tại một hàng, ta phải sử dụng kết quả ở hàng bên phải nó.Đó là một cách thực hành tốt để tập thói quen lưu trữ vị trí các chữ số. Ở các phần sau của cuốn sách, khi thực hiện phép nhân hai số có nhiều chữ số, ta sẽ thấy rằng cần phải dành một sự tập trung nhất định để nhận biết vị trí những hàng chúng ta đang làm việc. Cách thực hiện phép nhân với 5 là một rèn luyện nhỏ. Bạn hãy thực hiện cấc phép tính nhân 5 theo cách đã mô tả ở trên: 
Kết quả là: 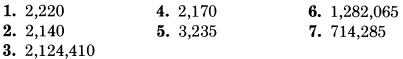
Còn tiếp
School@net
|

 THỰC HIỆN PHÉP NHÂN VỚI NĂM, SÁU VÀ BẢY
THỰC HIỆN PHÉP NHÂN VỚI NĂM, SÁU VÀ BẢY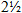 , tuy nhiên chúng ta không cần sử dụng phân số. Tương tự “một nửa” của 3 là 1, và “một nửa” của 1 là 0. Tất nhiên, “một nửa” của 4 là 2, và các số chắn khác cũng tương tự vậy.
, tuy nhiên chúng ta không cần sử dụng phân số. Tương tự “một nửa” của 3 là 1, và “một nửa” của 1 là 0. Tất nhiên, “một nửa” của 4 là 2, và các số chắn khác cũng tương tự vậy.