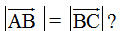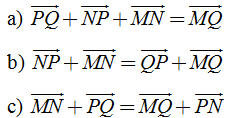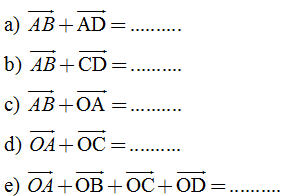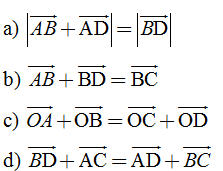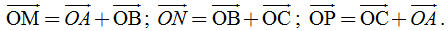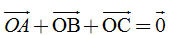1. Định nghĩa tổng của hai vectơ Hình 8 mô tả một vật được dời sang vị trí mới sao cho các điểm A, M, … của vật được dời đến các điểm A’, M’, … mà 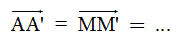 Khi đó ta nói rằng: Vật được “tịnh tiến’ theo vectơ Khi đó ta nói rằng: Vật được “tịnh tiến’ theo vectơ 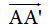 . . 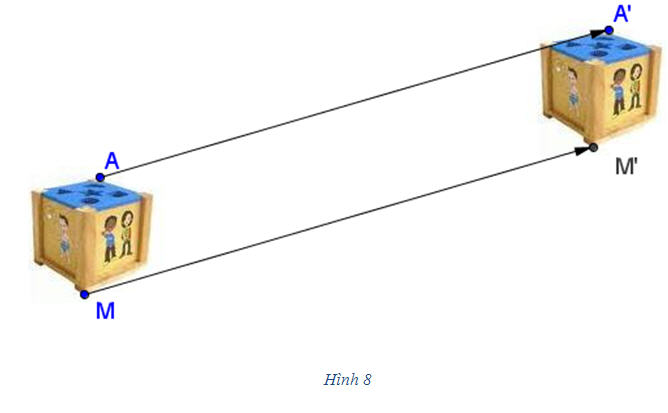 Tải trực tiếp tệp hình học động: L10_nc_ch1_h8.ggb Xem trực tiếp hình vẽ động trên màn hình. ?1 Trên hình 9, chuyển động của một vật được mô tả như sau: Từ vị trí (I), nó được tịnh tiến theo vectơ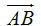 để đến vị trí (II). Sau đó nó lại được tịnh tiến một lần nữa theo vectơ để đến vị trí (II). Sau đó nó lại được tịnh tiến một lần nữa theo vectơ 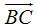 để đến vị trí (III). để đến vị trí (III). Vật có thể được tịnh tiến chỉ một lần để từ vị trí (I) đến vị trí (III) hay không? Nếu có, thì tịnh tiến theo vectơ nào? 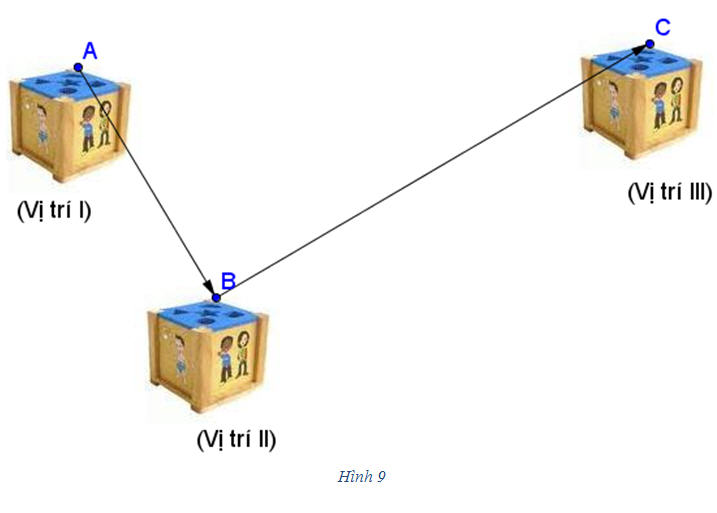
Tải trực tiếp tệp hình học động: L10_nc_ch1_h9.ggb Xem trực tiếp hình vẽ động trên màn hình. Như vậy có thể nói: Tịnh tiến theo vectơ 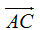 “bằng” tịnh tiến theo vectơ “bằng” tịnh tiến theo vectơ 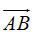 rồi tịnh tiến theo vectơ rồi tịnh tiến theo vectơ 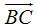 . . Trong Toán học, những điều trình bày trên đây được nói một cách ngắn gọn Vectơ 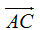 là tổng của hai vectơ là tổng của hai vectơ 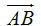 và và 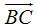 . . Ta đi đến định nghĩa (h. 10) Cho hai vectơ 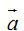 và và 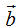 . Lấy một điểm A nào đó rồi xác định các điểm B và C sao cho . Lấy một điểm A nào đó rồi xác định các điểm B và C sao cho 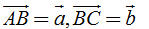 . Khi đó vectơ . Khi đó vectơ 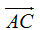 được gọi là tổng của hai vectơ được gọi là tổng của hai vectơ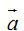 và và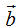 . Kí hiệu . Kí hiệu 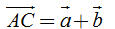 Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ. 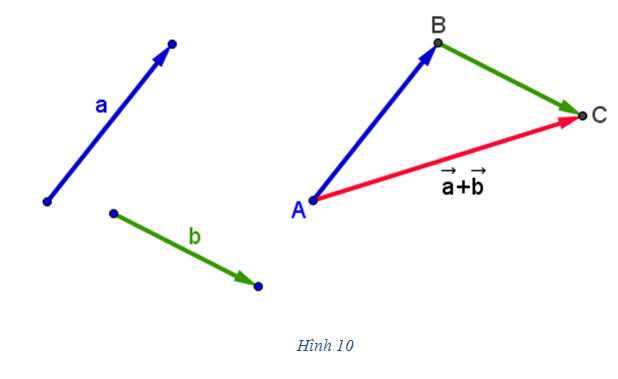
Tải trực tiếp tệp hình học động: L10_nc_ch1_h10.ggb Xem trực tiếp hình vẽ động trên màn hình.  1. Hãy vẽ một tam giác ABC, rồi xác định các vectơ tổng sau đây 1. Hãy vẽ một tam giác ABC, rồi xác định các vectơ tổng sau đây 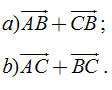
 2. Hãy vẽ hình bình hành ABCD với tâm O (O là giao điểm hai đường chéo). Hãy viết vectơ 2. Hãy vẽ hình bình hành ABCD với tâm O (O là giao điểm hai đường chéo). Hãy viết vectơ 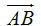 dưới dạng tổng của hai vectơ mà các điểm mút của chúng được lấy trong năm điểm A, B, C, D, O. dưới dạng tổng của hai vectơ mà các điểm mút của chúng được lấy trong năm điểm A, B, C, D, O. Các tính chất của phép cộng vectơ  3. Chúng ta biết rằng phép cộng hai số có tính chất giao hoán. Đối với phép cộng hai vectơ, tính chất đó có đúng hay không? Hãy kiểm chứng bằng hình vẽ. 3. Chúng ta biết rằng phép cộng hai số có tính chất giao hoán. Đối với phép cộng hai vectơ, tính chất đó có đúng hay không? Hãy kiểm chứng bằng hình vẽ.  4. Hãy vẽ các vectơ 4. Hãy vẽ các vectơ 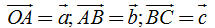 như trên hình 11. Trên hình vẽ đó như trên hình 11. Trên hình vẽ đó a) Hãy chỉ ra vectơ nào là vectơ, 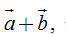 và do đó, vectơ nào là vectơ và do đó, vectơ nào là vectơ 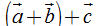 . . b) Hãy chỉ ra vectơ nào là vectơ 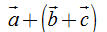 , và do đó, vectơ nào là vectơ , và do đó, vectơ nào là vectơ 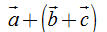 . . c) Từ đó có thể rút ra kết luận gì? 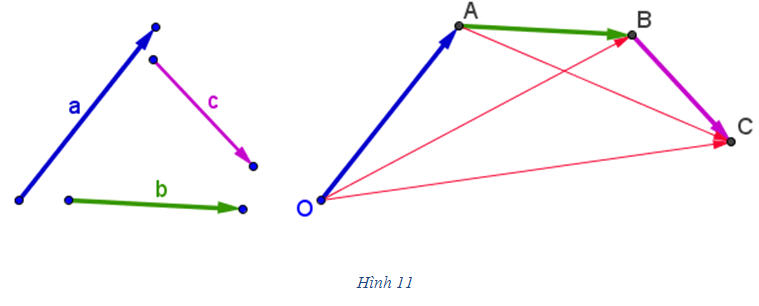
Tải trực tiếp tệp hình học động: L10_nc_ch1_h11.ggb Xem trực tiếp hình vẽ động trên màn hình. Từ các hoạt động trên, chúng ta suy ra các tính chất sau đây của phép cộng vectơ (cũng giống như các tính chất của phép cộng các số) 
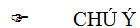
Do tính chất 2, các vectơ 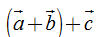 và và 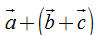 bằng nhau, bởi vậy, từ nay chúng được viết một cách đơn giản là bằng nhau, bởi vậy, từ nay chúng được viết một cách đơn giản là 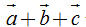 , và gọi là tổng của ba vectơ , và gọi là tổng của ba vectơ 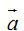 , , 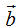 , , 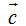 . . 3. Các quy tắc cần nhớ Từ định nghĩa tổng của hai vectơ ta suy ra hai quy tắc sau đây 
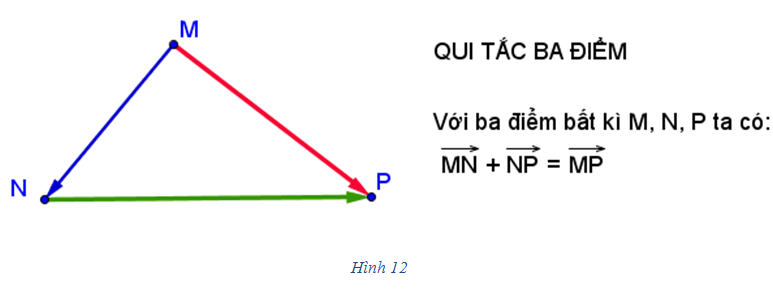
Tải trực tiếp tệp hình học động: L10_nc_ch1_h12.ggb Xem trực tiếp hình vẽ động trên màn hình. 
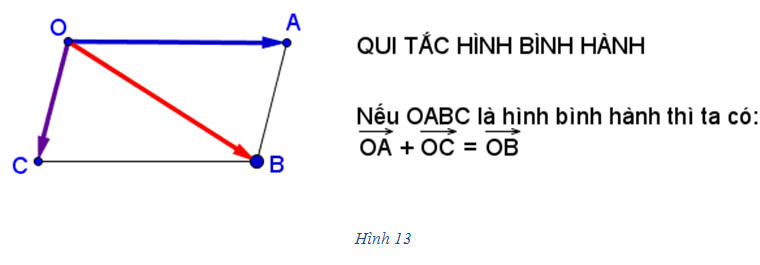
Tải trực tiếp tệp hình học động: L10_nc_ch1_h13.ggb Xem trực tiếp hình vẽ động trên màn hình. ?2. a) Hãy giải thích tại sao ta có quy tắc hình bình hành. b) Hãy giải thích tại sao ta có 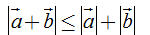 Bài toán 1. Chứng minh rằng với bốn điểm bất kì A, B, C, D ta có 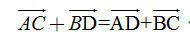 Giải. Dùng quy tắc ba điểm ta có thể viết 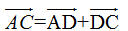 . Bởi vậy . Bởi vậy 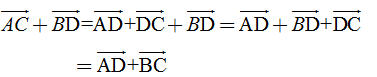
 5. Dùng quy tắc ba điểm, ta cũng có thể viết 5. Dùng quy tắc ba điểm, ta cũng có thể viết 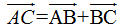 . Hãy tiếp tục để có một cách chứng minh khác của bài toán 1. . Hãy tiếp tục để có một cách chứng minh khác của bài toán 1. Bài toán 2. Cho tam giác đều ABC có cạnh bằng a. Tính độ dài của vectơ tổng 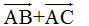 . . Giải. Ta lấy điểm D sao cho ABDC là hình bình hành (h. 14). 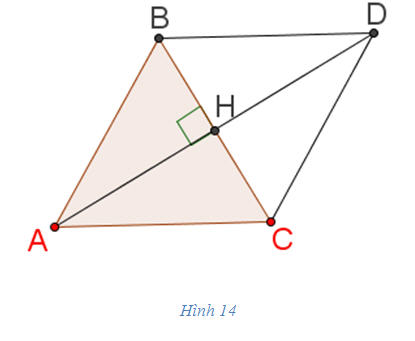
Tải trực tiếp tệp hình học động: L10_nc_ch1_h14.ggb Xem trực tiếp hình vẽ động trên màn hình. Theo quy tắc hình bình hành ta có 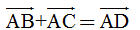 Vậy 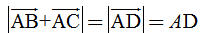 Vì ABC là tam giác đều nên ABDC là hình thoi và độ dài AD bằng hai lần đường cao AH của tam giác ABC, do đó: 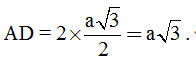 Tóm lại: 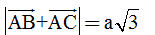
Bài toán 3. a) Gọi M là trung điểm đoạn thẳng AB. Chứng minh rằng 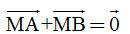 . . b) Gọi G là trọng tâm tam giác ABC. Chứng minh rằng 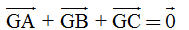 . . Giải. a) Theo quy tắc ba điểm, ta có 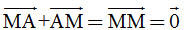 . Mặt khác, vì M là trung điểm của AB nên . Mặt khác, vì M là trung điểm của AB nên 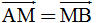 . Vậy . Vậy 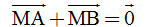 b) (h. 15) Trọng tâm G nằm trên trung tuyến CM và GC = 2GM. Để tìm tổng 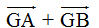 , ta dựng hình bình hành AGBC’. Muốn v, ta chỉ cần lấy điểm C’ sao cho M là trung điểm GC’. , ta dựng hình bình hành AGBC’. Muốn v, ta chỉ cần lấy điểm C’ sao cho M là trung điểm GC’. Khi đó 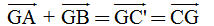 . Bởi vậy . Bởi vậy 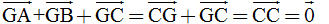 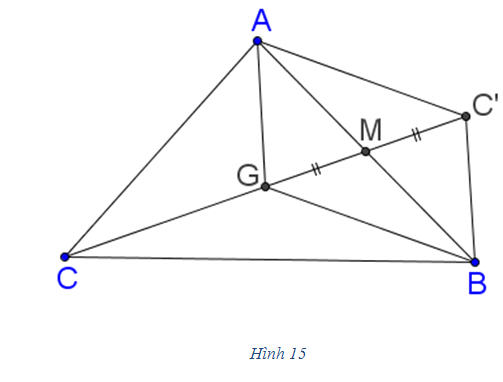
Tải trực tiếp tệp hình học động: L10_nc_ch1_h15.ggb Xem trực tiếp hình vẽ động trên màn hình. ?3 Trong lời giải của Bài toán 3, ta đã dùng đẳng thức 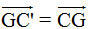 . Hãy giải thích tại sao có đẳng thức đó. . Hãy giải thích tại sao có đẳng thức đó. 
Quy tắc hình bình hành thường được áp dụng trong Vật lí để xác định hợp lực của hai lực cùng tác dụng lên một vật. Trên hình 16, có hai lực 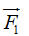 và và 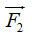 cùng tác dụng vào một vật tại điểm O. Khi đó có thể xem vật chịu tác dụng của lực cùng tác dụng vào một vật tại điểm O. Khi đó có thể xem vật chịu tác dụng của lực 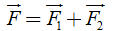 , là hợp lực c hai lực , là hợp lực c hai lực 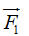 và và 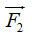 . Lực . Lực 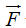 được xác định theo quy tắc hình bình hành. được xác định theo quy tắc hình bình hành. 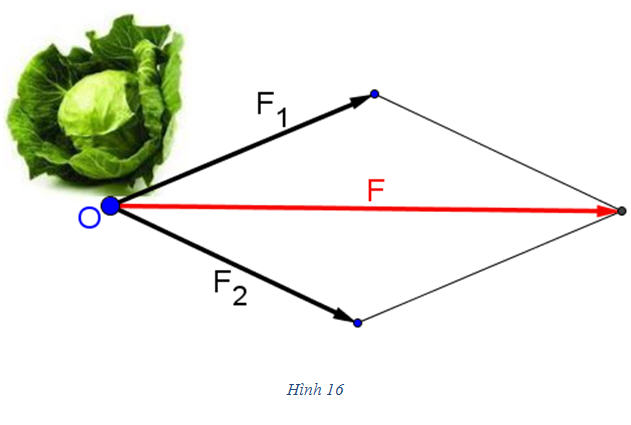
Tải trực tiếp tệp hình học động: L10_nc_ch1_h16.ggb Xem trực tiếp hình vẽ động trên màn hình.
Câu hỏi và bài tập
6. Chứng minh rằng nếu 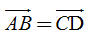 thì thì 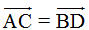 7. Tứ giác ABCD là hình gì nếu 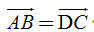 thì thì 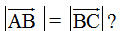 8. Cho bốn điểm bất kì M, N, P, Q. Chứng minh các đẳng thức sau 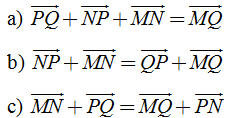
9. Các hệ thức sau đây đúng hay sai (với mọi 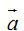 và và 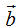 )? )?  10. Cho hình bình hành ABCD với tâm O. Mỗi khẳng định sau đây đúng hay sai? 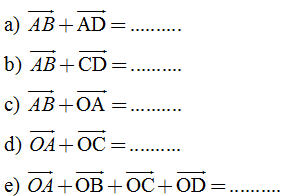
11. Cho hình bình hành ABCD với tâm O. Mỗi khẳng định sau đây đúng hay sai? 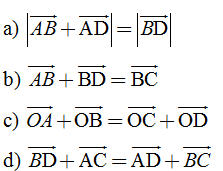
12. Cho tam giác đều ABC nội tiếp đường tròn tâm O. a) Hãy xác định các điểm M, N, P sao cho: 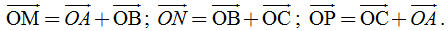
b) Chứng minh rằng: 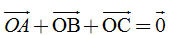 13. Cho hai lực 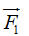 và và 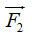 cùng có điểm đặt tại O (h. 17). Tìm cường độ lực tổng hợp của chúng trong các trường hợp sau: cùng có điểm đặt tại O (h. 17). Tìm cường độ lực tổng hợp của chúng trong các trường hợp sau: a) 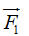 và và 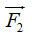 đều có cường độ là 100N, góc hợp bởi đều có cường độ là 100N, góc hợp bởi 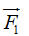 và và 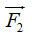 bằng 1200 (h. 17a); bằng 1200 (h. 17a); b) Cường độ của 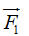 là 40N, của là 40N, của 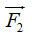 là 30N và góc giữa là 30N và góc giữa 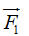 và và 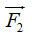 bằng 900 (h. 17b). bằng 900 (h. 17b). 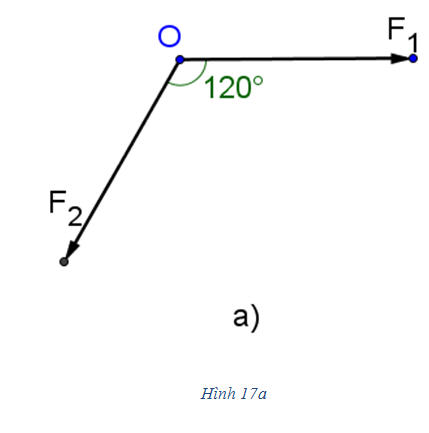
Tải trực tiếp tệp hình học động: L10_nc_ch1_h17a.ggb Xem trực tiếp hình vẽ động trên màn hình. 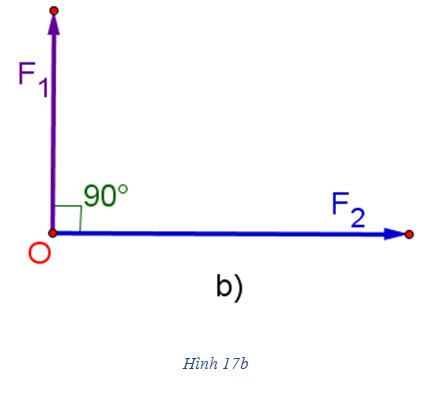
Tải trực tiếp tệp hình học động: L10_nc_ch1_h17b.ggb Xem trực tiếp hình vẽ động trên màn hình.
Schoolnet
|

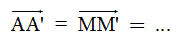 Khi đó ta nói rằng: Vật được “tịnh tiến’ theo vectơ
Khi đó ta nói rằng: Vật được “tịnh tiến’ theo vectơ 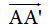 .
.
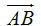 để đến vị trí (II). Sau đó nó lại được tịnh tiến một lần nữa theo vectơ
để đến vị trí (II). Sau đó nó lại được tịnh tiến một lần nữa theo vectơ 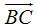 để đến vị trí (III).
để đến vị trí (III).
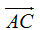 “bằng” tịnh tiến theo vectơ
“bằng” tịnh tiến theo vectơ 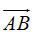 rồi tịnh tiến theo vectơ
rồi tịnh tiến theo vectơ 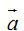 và
và 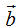 . Lấy một điểm A nào đó rồi xác định các điểm B và C sao cho
. Lấy một điểm A nào đó rồi xác định các điểm B và C sao cho 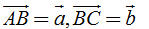 . Khi đó vectơ
. Khi đó vectơ 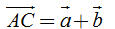

 1. Hãy vẽ một tam giác ABC, rồi xác định các vectơ tổng sau đây
1. Hãy vẽ một tam giác ABC, rồi xác định các vectơ tổng sau đây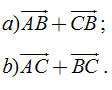
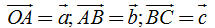 như trên hình 11. Trên hình vẽ đó
như trên hình 11. Trên hình vẽ đó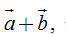 và do đó, vectơ nào là vectơ
và do đó, vectơ nào là vectơ 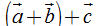 .
.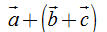 , và do đó, vectơ nào là vectơ
, và do đó, vectơ nào là vectơ 

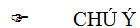
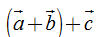 và
và 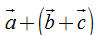 bằng nhau, bởi vậy, từ nay chúng được viết một cách đơn giản là
bằng nhau, bởi vậy, từ nay chúng được viết một cách đơn giản là 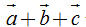 , và gọi là tổng của ba vectơ
, và gọi là tổng của ba vectơ 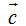 .
.



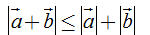
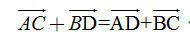
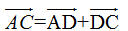 . Bởi vậy
. Bởi vậy 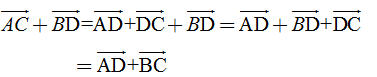
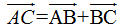 . Hãy tiếp tục để có một cách chứng minh khác của bài toán 1.
. Hãy tiếp tục để có một cách chứng minh khác của bài toán 1.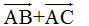 .
.
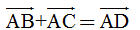
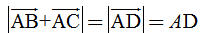
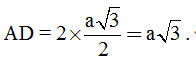
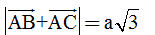
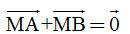 .
.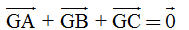 .
.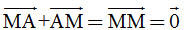 . Mặt khác, vì M là trung điểm của AB nên
. Mặt khác, vì M là trung điểm của AB nên 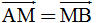 . Vậy
. Vậy 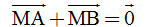
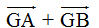 , ta dựng hình bình hành AGBC’. Muốn v, ta chỉ cần lấy điểm C’ sao cho M là trung điểm GC’.
, ta dựng hình bình hành AGBC’. Muốn v, ta chỉ cần lấy điểm C’ sao cho M là trung điểm GC’.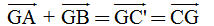 . Bởi vậy
. Bởi vậy 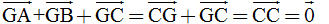

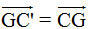 . Hãy giải thích tại sao có đẳng thức đó.
. Hãy giải thích tại sao có đẳng thức đó.
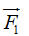 và
và 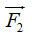 cùng tác dụng vào một vật tại điểm O. Khi đó có thể xem vật chịu tác dụng của lực
cùng tác dụng vào một vật tại điểm O. Khi đó có thể xem vật chịu tác dụng của lực 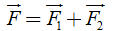 , là hợp lực c hai lực
, là hợp lực c hai lực 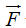 được xác định theo quy tắc hình bình hành.
được xác định theo quy tắc hình bình hành.
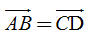 thì
thì 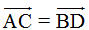
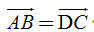 thì
thì