 Tải trực tiếp tệp hình học động: L10_nc_ch1_h27.ggb Xem trực tiếp hình vẽ động trên màn hình.
Điểm O gọi là gốc tọa độ, vectơ 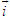 gọi là vectơ đơn vị của trục tọa độ. gọi là vectơ đơn vị của trục tọa độ. Trục tọa độ như vậy được kí hiệu là (O; 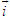 ). Ta lấy điểm I sao cho ). Ta lấy điểm I sao cho 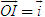 , tia OI còn được kí hiệu là Ox, tia đối của tia Ox là Ox’. Khi đó trục (O; , tia OI còn được kí hiệu là Ox, tia đối của tia Ox là Ox’. Khi đó trục (O; 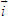 ) còn gọi là trục x’Ox hay trục Ox (h. 27). ) còn gọi là trục x’Ox hay trục Ox (h. 27). Tọa độ của vectơ và của điểm trên trục Cho vectơ 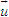 nằm trên trục (O; nằm trên trục (O; 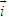 ). Khi đó có số a xác định để ). Khi đó có số a xác định để 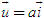 . Số a như thế gọi là tọa độ của vectơ . Số a như thế gọi là tọa độ của vectơ 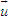 đối với trục (O; đối với trục (O; 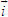 ). ). Cho điểm M nằm trên trục (O; 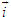 ). Khi đó có số m xác định để ). Khi đó có số m xác định để 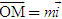 . Số m như thế gọi là tọa độ của điểm m đối với trục (O; . Số m như thế gọi là tọa độ của điểm m đối với trục (O; 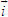 ) (cũng là tọa độ của vectơ ) (cũng là tọa độ của vectơ 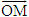 ). ).  1.Trên trục Ox cho hai điểm A và B lần lượt có tọa độ là a và b. Tìm tọa độ của vectơ 1.Trên trục Ox cho hai điểm A và B lần lượt có tọa độ là a và b. Tìm tọa độ của vectơ 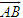 và vectơ và vectơ 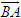 . Tìm tọa độ trung điểm của đoạn thẳng AB. . Tìm tọa độ trung điểm của đoạn thẳng AB. Độ dài số của vectơ trên trục Nếu hai điểm A, B nằm trên trục Ox thì tọa độ của vectơ 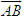 được kí hiệu là được kí hiệu là 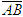 và gọi là độ đài đại số của vectơ và gọi là độ đài đại số của vectơ 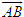 trên trục Ox. trên trục Ox. Như vậy 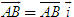 . . Từ định nghĩa trên ta suy ra các khẳng định sau đây: trên trục số, 1) Hai vectơ 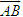 và và 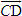 bằng nhau khi và chỉ khi bằng nhau khi và chỉ khi 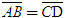 (hiển nhiên). (hiển nhiên). 2) Hệ thức 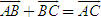 tương đương với hệ thức tương đương với hệ thức 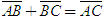 (hệ thức Saclơ). (hệ thức Saclơ). Thật vậy, 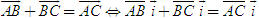 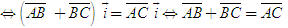 2. Hệ trục tọa độ Trên hình 28, ta có một hệ trục tọa độ vuông góc. Nó bao gồm hai trục tọa độ Ox và Oy vuông góc với nhau. 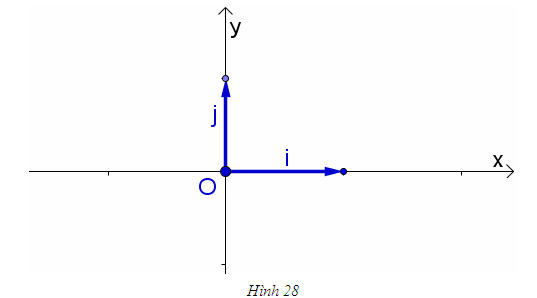 Tải trực tiếp tệp hình học động: L10_nc_ch1_h28.ggb Xem trực tiếp hình vẽ động trên màn hình.
Vectơ đơn vị trên trục Ox là 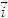 , vectơ đơn vị trên trục Oy là , vectơ đơn vị trên trục Oy là 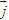 . . Điểm O gọi là gốc tọa độ. Trục Ox gọi là trục hoành, trục Oy gọi là trục tung. Hệ trục tọa độ vuông góc như trên còn gọi đơn giản là hệ trục tọa độ và thường được kí hiệu là Oxy hay (O;  , , 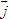 ). ). 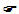 CHÚ Ý CHÚ Ý Khi trong mặt phẳng đã cho (hay đã chọn) một hệ trục tọa độ, ta sẽ gọi mặt phẳng đó là mặt phẳng tọa độ. 3. Tọa độ của vectơ đối với hệ trục tọa độ  2.Quan sát hình 29. Hãy biểu thị mỗi vectơ 2.Quan sát hình 29. Hãy biểu thị mỗi vectơ 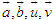 qua hai vectơ qua hai vectơ 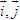 dưới dạng dưới dạng 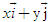 với x, y là hai số thực nào đó. với x, y là hai số thực nào đó. 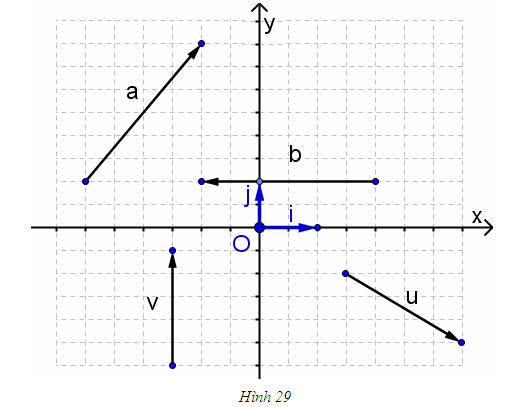 Tải trực tiếp tệp hình học động: L10_nc_ch1_h29.ggb Xem trực tiếp hình vẽ động trên màn hình.
ĐỊNH NGHĨA Đối với hệ trục tọa độ (O; 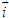 , , 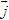 ), nếu ), nếu 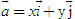 thì cặp số (x ; y) được gọi là tọa độ của vectơ thì cặp số (x ; y) được gọi là tọa độ của vectơ 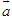 , kí hiệu là , kí hiệu là 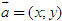 hay hay 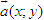 . Số thứ nhất x gọi là hoành độ, số thứ hai y gọi là tung độcủa vectơ . Số thứ nhất x gọi là hoành độ, số thứ hai y gọi là tung độcủa vectơ 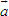 . . ?1. a) Tìm tọa độ của các vectơ 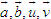 trên hình 29. trên hình 29. b) Đối với hệ trục tọa độ (O; 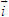 , , 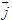 ), hãy chỉ ra tọa độ của các vectơ . ), hãy chỉ ra tọa độ của các vectơ . 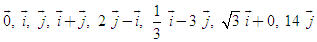 Nhận xét. Từ định nghĩa tọa độ của vectơ, ta thấy hai vectơ bằng nhau khi và chỉ khi chúng có cùng tọa độ, nghĩa là 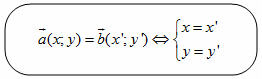 4. Biểu thức tọa độ của các phép toán vectơ Trong mục này ta nói về biểu thức tọa độ của các phép toán vectơ sau phép cộng, phép trừ vectơ và phép nhân vectơ với số.  3.Cho hai vectơ 3.Cho hai vectơ 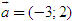 và và 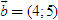 . . a) Hãy biểu thị các vectơ 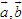 qua hai vectơ qua hai vectơ 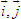 . . b) Tìm tọa độ của các vectơ 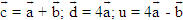 . . Một cách tổng quát, ta có  ?2. Mỗi cặp vectơ sau có cùng phương không? a) 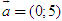 và và 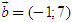 ; ; b) 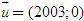 và và 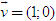 ; ; c) 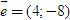 và và 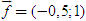 d) 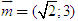 và và 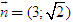 5. Tọa độ của điểm Trong mặt phẳng tọa độ Oxy, mỗi điểm M được xác định hoàn toàn bởi vectơ 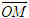 . Do vậy, nếu biết tọa độ của vectơ . Do vậy, nếu biết tọa độ của vectơ 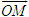 thì điểm M sẽ được xác định. Vì lẽ đó người ta định nghĩa thì điểm M sẽ được xác định. Vì lẽ đó người ta định nghĩa Trong mặt phẳng tọa độ Oxy, tọa độ của vectơ 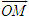 được gọi là tọa độ của điểm M. được gọi là tọa độ của điểm M. Như vậy, cặp số (x ; y) là tọa độ của điểm M khi và chỉ khi 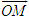 = (x ; y). Khi đó ta viết M(x ; y) hoặc M = (x ; y). = (x ; y). Khi đó ta viết M(x ; y) hoặc M = (x ; y). Số x gọi là hoành độ của điểm M, số y gọi là tung độ của điểm M. Nhận xét. (h. 30) Gọi H, K lần lượt là hình chiếu của M trên Ox và Oy. Khi đó, nếu M = (x ; y) thì 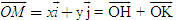 . Suy ra . Suy ra 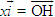 hay hay 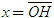 ; ; 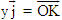 hay hay 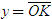 . . 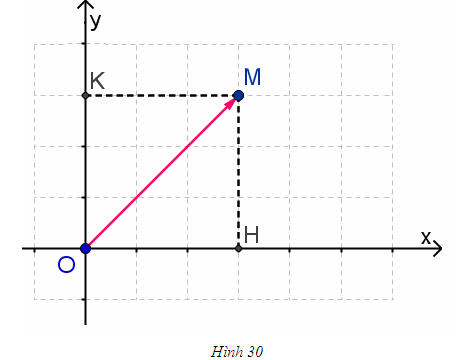 Tải trực tiếp tệp hình học động: L10_nc_ch1_h30.ggb Xem trực tiếp hình vẽ động trên màn hình.
 4.Trên hình 31 4.Trên hình 31 a) Tọa độ mỗi điểm O, A, B, C, D bằng bao nhiêu? b) Hãy tìm điểm E có tọa độ (4; -4). c) Tìm tọa độ vectơ 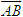 . . 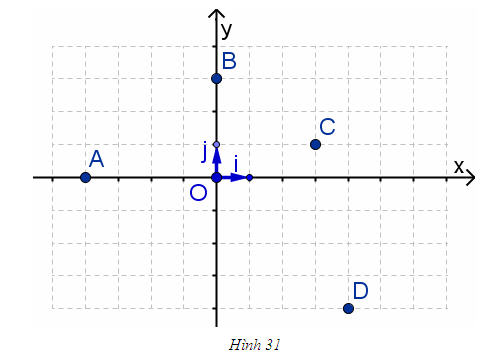 Tải trực tiếp tệp hình học động: L10_nc_ch1_h31.ggb Xem trực tiếp hình vẽ động trên màn hình.
Tổng quát, ta có 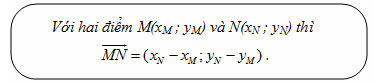 ?3. Hãy giải thích vì sao có kết quả trên.  CHÚ Ý CHÚ Ý Để thuận tiện, ta thường dùng kí hiệu (xM ; yM) để chỉ tọa độ của điểm M. 6. Tọa độ trung điểm của đoạn thẳng và tọa độ của trọng tâm tam giác  5.Trong mặt phẳng tọa độ Oxy, cho hai điểm M(xM ; yM), N(xN; yN). Gọi P là trung điểm của đoạn thẳng MN. 5.Trong mặt phẳng tọa độ Oxy, cho hai điểm M(xM ; yM), N(xN; yN). Gọi P là trung điểm của đoạn thẳng MN. a) Hãy biểu thị vectơ 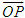 qua hai vectơ qua hai vectơ 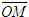 và và 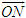 . . b) Từ đó hãy tìm tọa độ điểm P theo tọa độ của M và N. Vậy ta có 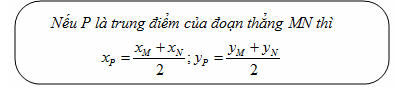  6.Tìm tọa độ điểm M’ đối xứng với điểm M(7 ; -3) qua điểm A(1 ; 1) 6.Tìm tọa độ điểm M’ đối xứng với điểm M(7 ; -3) qua điểm A(1 ; 1)  7.Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với trọng tâm G. 7.Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với trọng tâm G. a) Hãy viết hệ thức giữa các vectơ 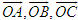 và và 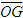 . . b) Từ đó suy ra tọa độ của G theo tọa độ của A, B, C. Vậy ta có 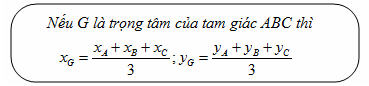 Ví dụ. Trong mặt phẳng tọa độ Oxy, cho các điểm A(2 ; 0), B(0 ; 4), C(1 ; 3). a) Chứng minh A, B, C là ba đỉnh của một tam giác. b) Tìm tọa độ của trọng tâm tam giác ABC. Giải. a) Ta có 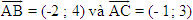 Do Do 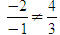 nên nên 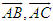 không cùng phương, suy ra A, B, C không thẳng hàng và chúng là ba đỉnh của một tam giác. không cùng phương, suy ra A, B, C không thẳng hàng và chúng là ba đỉnh của một tam giác. b) Ta có 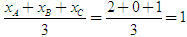 và và 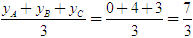 . . Vậy tọa độ của trọng tâm tam giác ABC là 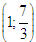 . . Câu hỏi và bài tập 29. Trong mặt phẳng tọa độ, mỗi mệnh đề sau đúng hay sai? a) Hai vectơ 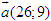 và và 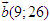 bằng nhau. bằng nhau. b) Hai vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau. c) Hai vectơ đối nhau thì chúng có hoành độ đối nhau. d) Vectơ 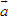 cùng phương với vectơ cùng phương với vectơ 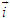 nếu nếu 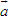 có hoành độ bằng 0. có hoành độ bằng 0. e) Vectơ 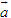 có hoành độ bằng 0 thì cùng phương với vectơ có hoành độ bằng 0 thì cùng phương với vectơ 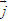 . . 30. Tìm tọa độ của các vectơ sau trong mặt phẳng tọa độ 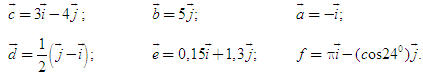 31. Cho 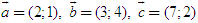 . . a) Tìm tọa độ của vectơ 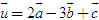 . . b) Tìm tọa độ của vectơ 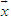 sao cho sao cho 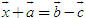 . . c) Tìm các số k, l để 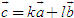 . . 32. Cho 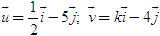 . . Tìm các giá trị của k để hai vectơ 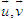 cùng phương. cùng phương. 33. Trong các mệnh đề sau, mệnh đề nào đúng? a) Tọa độ của điểm A bằng tọa độ của vectơ 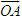 , với O là gốc tọa độ. , với O là gốc tọa độ. b) Hoành độ của một điểm bằng 0 thì điểm đó nằm trên trục hoành. c) Điểm A nằm trên trục tung thì A có hoành độ bằng 0. d) P là trung điểm của đoạn thẳng AB khi và chỉ khi hoành độ điểm P bằng trung bình cộng các hoành độ của hai điểm A, B. e) Tứ giác ABCD là hình bình hành khi và chỉ khi xA + xC = xB + xD và yA + yC = yB + yD. 34. Trong mặt phẳng tọa độ, cho ba điểm A(-3 ; 4), B(1 ; 1), C(9 ; -5). a) Chứng minh ba điểm A, B, C thẳng hàng. b) Tìm tọa độ điểm D sao cho A là trung điểm của BD. c) Tìm tọa độ điểm E trên trục Ox sao cho A, B, E thẳng hàng. 35. Cho điểm M(x ; y). Tìm tọa độ của các điểm a) M1 đối xứng với M qua trục Ox; b) M2 đối xứng với M qua trục Oy; c)M3 đối xứng với M qua gốc tọa độ O; 36. Trong mặt phẳng tọa độ, cho ba điểm A(-4 ; 1), B(2 ; 4), C(2 ; -2). a) Tìm tọa độ trọng tâm G của tam giác ABC. b) Tìm tọa độ điểm D sao cho C là trọng tâm tam giác ABD. c) Tìm tọa độ điểm E sao cho ABCE là hình bình hành.
School@net
|

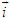 có độ dài bằng 1.
có độ dài bằng 1.
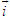 gọi là vectơ đơn vị của trục tọa độ.
gọi là vectơ đơn vị của trục tọa độ.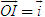 , tia OI còn được kí hiệu là Ox, tia đối của tia Ox là Ox’. Khi đó trục (O;
, tia OI còn được kí hiệu là Ox, tia đối của tia Ox là Ox’. Khi đó trục (O; 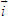 ) còn gọi là trục x’Ox hay trục Ox (h. 27).
) còn gọi là trục x’Ox hay trục Ox (h. 27).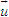 nằm trên trục (O;
nằm trên trục (O; 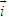 ). Khi đó có số a xác định để
). Khi đó có số a xác định để 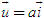 . Số a như thế gọi là tọa độ của vectơ
. Số a như thế gọi là tọa độ của vectơ 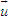 đối với trục (O;
đối với trục (O; 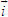 ).
).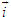 ). Khi đó có số m xác định để
). Khi đó có số m xác định để 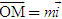 . Số m như thế gọi là tọa độ của điểm m đối với trục (O;
. Số m như thế gọi là tọa độ của điểm m đối với trục (O; 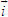 ) (cũng là tọa độ của vectơ
) (cũng là tọa độ của vectơ 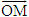 ).
). 1.Trên trục Ox cho hai điểm A và B lần lượt có tọa độ là a và b. Tìm tọa độ của vectơ
1.Trên trục Ox cho hai điểm A và B lần lượt có tọa độ là a và b. Tìm tọa độ của vectơ 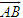 và vectơ
và vectơ 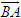 . Tìm tọa độ trung điểm của đoạn thẳng AB.
. Tìm tọa độ trung điểm của đoạn thẳng AB.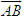 được kí hiệu là
được kí hiệu là 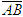 và gọi là độ đài đại số của vectơ
và gọi là độ đài đại số của vectơ 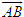 trên trục Ox.
trên trục Ox.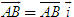 .
.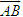 và
và 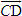 bằng nhau khi và chỉ khi
bằng nhau khi và chỉ khi 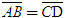 (hiển nhiên).
(hiển nhiên).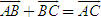 tương đương với hệ thức
tương đương với hệ thức 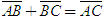 (hệ thức Saclơ).
(hệ thức Saclơ).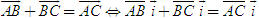
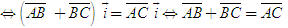

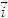 , vectơ đơn vị trên trục Oy là
, vectơ đơn vị trên trục Oy là 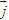 .
. ,
, 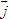 ).
). CHÚ Ý
CHÚ Ý 2.Quan sát hình 29. Hãy biểu thị mỗi vectơ
2.Quan sát hình 29. Hãy biểu thị mỗi vectơ 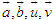 qua hai vectơ
qua hai vectơ 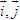 dưới dạng
dưới dạng 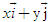 với x, y là hai số thực nào đó.
với x, y là hai số thực nào đó.
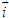 ,
, 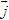 ), nếu
), nếu 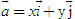 thì cặp số (x ; y) được gọi là tọa độ của vectơ
thì cặp số (x ; y) được gọi là tọa độ của vectơ 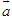 , kí hiệu là
, kí hiệu là 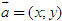 hay
hay 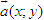 . Số thứ nhất x gọi là hoành độ, số thứ hai y gọi là tung độcủa vectơ
. Số thứ nhất x gọi là hoành độ, số thứ hai y gọi là tung độcủa vectơ 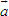 .
.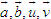 trên hình 29.
trên hình 29.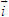 ,
, 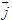 ), hãy chỉ ra tọa độ của các vectơ .
), hãy chỉ ra tọa độ của các vectơ .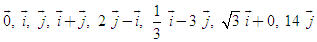
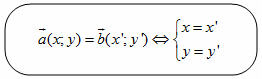
 3.Cho hai vectơ
3.Cho hai vectơ 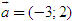 và
và 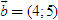 .
.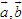 qua hai vectơ
qua hai vectơ 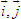 .
.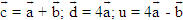 .
.
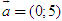 và
và 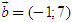 ;
;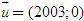 và
và 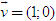 ;
;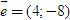 và
và 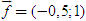
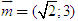 và
và 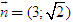
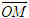 . Do vậy, nếu biết tọa độ của vectơ
. Do vậy, nếu biết tọa độ của vectơ 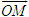 thì điểm M sẽ được xác định. Vì lẽ đó người ta định nghĩa
thì điểm M sẽ được xác định. Vì lẽ đó người ta định nghĩa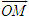 được gọi là tọa độ của điểm M.
được gọi là tọa độ của điểm M. 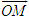 = (x ; y). Khi đó ta viết M(x ; y) hoặc M = (x ; y).
= (x ; y). Khi đó ta viết M(x ; y) hoặc M = (x ; y).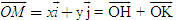 . Suy ra
. Suy ra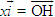 hay
hay 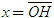 ;
;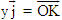 hay
hay 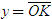 .
.
 4.Trên hình 31
4.Trên hình 31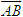 .
.
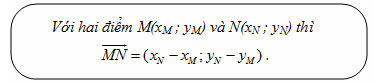
 CHÚ Ý
CHÚ Ý 5.Trong mặt phẳng tọa độ Oxy, cho hai điểm M(xM ; yM), N(xN; yN). Gọi P là trung điểm của đoạn thẳng MN.
5.Trong mặt phẳng tọa độ Oxy, cho hai điểm M(xM ; yM), N(xN; yN). Gọi P là trung điểm của đoạn thẳng MN.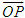 qua hai vectơ
qua hai vectơ 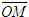 và
và 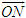 .
.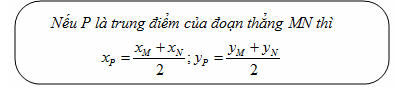
 6.Tìm tọa độ điểm M’ đối xứng với điểm M(7 ; -3) qua điểm A(1 ; 1)
6.Tìm tọa độ điểm M’ đối xứng với điểm M(7 ; -3) qua điểm A(1 ; 1) 7.Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với trọng tâm G.
7.Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với trọng tâm G.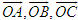 và
và  .
.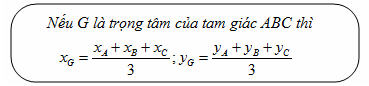
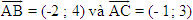 Do
Do 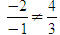 nên
nên 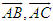 không cùng phương, suy ra A, B, C không thẳng hàng và chúng là ba đỉnh của một tam giác.
không cùng phương, suy ra A, B, C không thẳng hàng và chúng là ba đỉnh của một tam giác.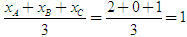 và
và 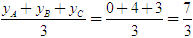 .
.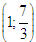 .
.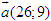 và
và 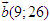 bằng nhau.
bằng nhau.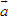 cùng phương với vectơ
cùng phương với vectơ 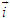 nếu
nếu 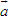 có hoành độ bằng 0.
có hoành độ bằng 0.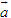 có hoành độ bằng 0 thì cùng phương với vectơ
có hoành độ bằng 0 thì cùng phương với vectơ 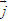 .
.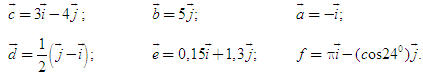
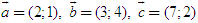 .
.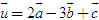 .
.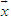 sao cho
sao cho 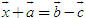 .
.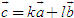 .
.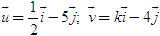 .
.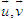 cùng phương.
cùng phương.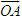 , với O là gốc tọa độ.
, với O là gốc tọa độ.



