1. Vectơ trong không gian Khái niệm vectơ và các phép toán vectơ đã được đề cập trong chương trình hình học lớp 10. Tuy nhiên, khi đó tất cả các vectơ mà chúng ta xem xét đều nằm trên cùng một mặt phẳng. Ở chương II, chúng ta đã làm quen với việc nghiên cứu hình học không gian mà đối tượng của nó là các hình có thể không cùng nằm trong một mặt phẳng. Chẳng hạn, tứ diện ABCD là một hình có tính chất đó và như thế các vectơ  không cùng nằm trong một mặt phẳng nào cả (h.82). không cùng nằm trong một mặt phẳng nào cả (h.82). 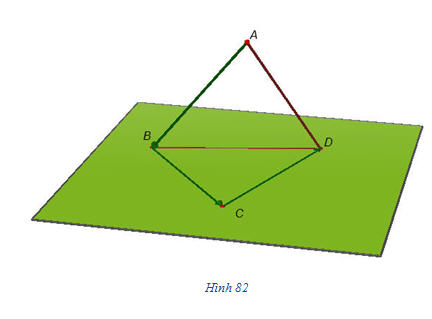
Tải trực tiếp tệp hình học động (Nhấn chuột phải vào liên kết rồi chọn Save As hoặc Lưu Liên Kết dưới dạng):L11_ch3_h82.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Trong chương này, chúng ta sẽ nói đến các vectơ trong không gian. Vectơ, các phép toán vectơ trong không gian được định nghĩa hoàn toàn giống như trong mặt phẳng, chúng cũng có các tính chất đã biết nên không nhắc lại. Sau đây, chúng ta nêu lên một số hoạt động và ví dụ nhằm mục đích ôn tập lại những kiến thức đã có về vectơ trong mặt phẳng để áp dụng vào không gian.  1 1
Cho hình hộp ABCD.A’B’C’D’ với tâm O (h.83). 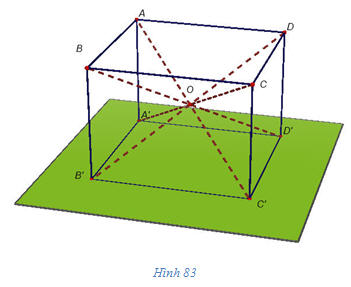
Tải trực tiếp tệp hình học động (Nhấn chuột phải vào liên kết rồi chọn Save As hoặc Lưu Liên Kết dưới dạng):L11_ch3_h83.cg3
Xem trực tiếp hình vẽ động trên màn hình.
a) Hãy chỉ ra trên hình 83 những vectơ bằng nhau khác vectơ 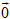 và kiểm tra tính đúng đắn của đẳng thức và kiểm tra tính đúng đắn của đẳng thức 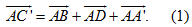 b) Chứng minh rằng 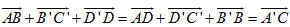
CHÚ Ý Công thức (1) gọi là quy tắc hình hộp (để tìm tổng của ba vectơ).  2 2
Cho tứ diện ABCD với trọng tâm G và các trung điểm các cạnh của nó (h.84). Hãy chỉ ra trên hình 84 những vectơ khác 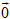 bằng nhau và kiểm tra xem đẳng thức bằng nhau và kiểm tra xem đẳng thức 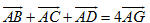 có đúng không? có đúng không? 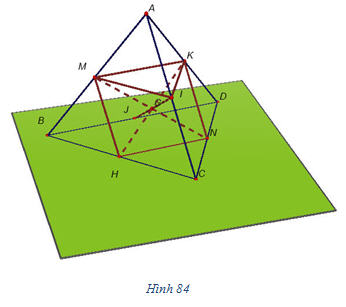
Tải trực tiếp tệp hình học động (Nhấn chuột phải vào liên kết rồi chọn Save As hoặc Lưu Liên Kết dưới dạng):L11_ch3_h84.cg3
Xem trực tiếp hình vẽ động trên màn hình.
 3 3
Cho hình lăng trụ ABC.A’B’C’. Đặt 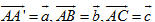 (h.85). (h.85). 1) Hãy biểu thị mỗi vectơ 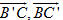 qua các vectơ qua các vectơ 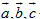 . . 2) Gọi G’ là trọng tâm tam giác A’B’C’. Biểu thị vectơ 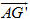 qua qua 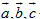 . . 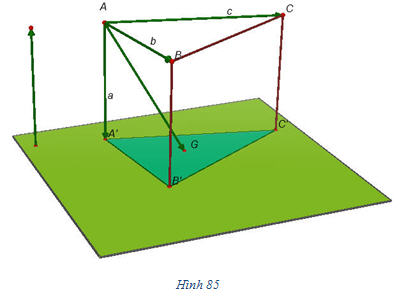
Tải trực tiếp tệp hình học động (Nhấn chuột phải vào liên kết rồi chọn Save As hoặc Lưu Liên Kết dưới dạng):L11_ch3_h85.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Ví dụ 1 Cho tứ diện ABCD 1. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng tỏ rằng: 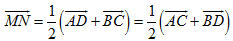
2. Chứng minh rằng điểm G là trọng tâm của tứ diện khi và chỉ khi một trong hai điều kiện sau xảy ra: 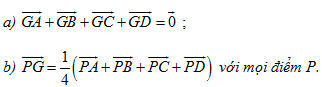
Giải (h.86) 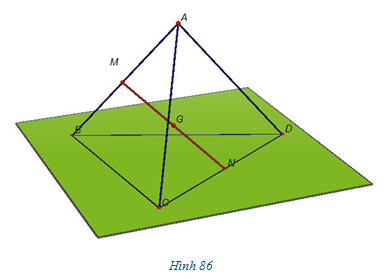
Tải trực tiếp tệp hình học động (Nhấn chuột phải vào liên kết rồi chọn Save As hoặc Lưu Liên Kết dưới dạng):L11_ch3_h86.cg3
Xem trực tiếp hình vẽ động trên màn hình.
1. Sử dụng quy tắc ba điểm, ta có: 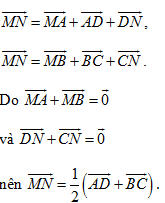
Tương tự như trên, ta có 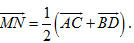
2. a) Ta có 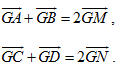
Điểm G là trọng tâm của tứ diện ABCD khi và chỉ khi 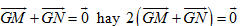
Điều này tương đương với 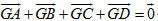 b) G là trọng tâm của tứ diện ABCD khi và chỉ khi 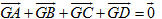
Điều này có nghĩa là với điểm P bất kì, ta có 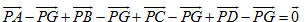
Hay: 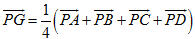
Ví dụ 2 Cho tứ diện ABCD có AB = c, CD = c’, AC = b, BD = b’, BC = a, AD = a’. Tính góc giữa các vectơ  và và  . . Giải. Ta có 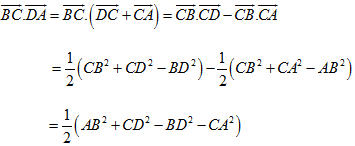
Từ đó góc 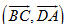 xác định bởi xác định bởi 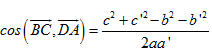
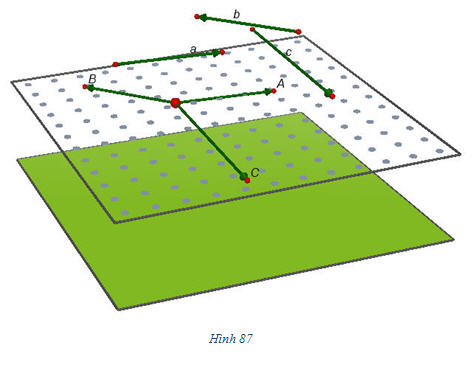
2. Sự đồng phẳng của các vectơ. Điều kiện để ba vectơ đồng phẳng Ta biết rằng, với hai đường thẳng phân biệt cho trước trong không gian, luôn có mặt phẳng song song với hai đường thẳng đó. Nhưng nói chung, không có mặt phẳng song song với ba đường thẳng phân biệt cho trước. Nếu có mặt phẳng như vậy thì ta nói rằng ba vectơ nằm trên ba đường thẳng ấy là đồng phẳng. ĐỊNH NGHĨA 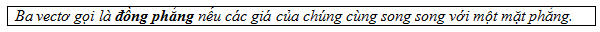
Tải trực tiếp tệp hình học động (Nhấn chuột phải vào liên kết rồi chọn Save As hoặc Lưu Liên Kết dưới dạng):L11_ch3_h87.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Trên hình 87, giá của ba vectơ 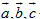 đều song song với mặt phẳng (P) nên ba vectơ đều song song với mặt phẳng (P) nên ba vectơ 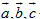 đồng phẳng. đồng phẳng. Nhận xét Từ định nghĩa trên, suy ra: Nếu ta vẽ 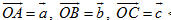 thì ba vectơ thì ba vectơ 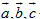 đồng phẳng khi và chỉ khi bốn điểm O, A, B, C cùng nằm trên một mặt phẳng hay ba đường thẳng OA, OB, OC cùng nằm trong một mặt phẳng. đồng phẳng khi và chỉ khi bốn điểm O, A, B, C cùng nằm trên một mặt phẳng hay ba đường thẳng OA, OB, OC cùng nằm trong một mặt phẳng. Bài toán 1 Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh rằng ba vectơ 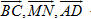 đồng phẳng. đồng phẳng.  4 (Để giải bài toán 1) 4 (Để giải bài toán 1)
Gọi P và Q lần lượt là trung điểm của AC và BD. Khi đó MPNQ là hình bình hành. Từ đó, hãy suy ra điều phải chứng minh (h.88). Điều kiện để ba vectơ đồng phẳng Từ định nghĩa ba vectơ đồng phẳng và sự khai triển một vectơ theo hai vectơ không cùng phương trong hình học phẳng, chúng ta có thể chứng minh được định lí sau (h.89). ĐỊNH LÍ 1 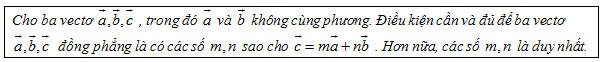
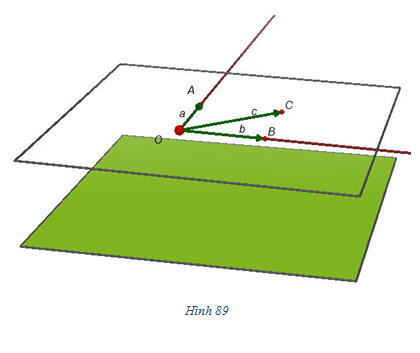
Tải trực tiếp tệp hình học động (Nhấn chuột phải vào liên kết rồi chọn Save As hoặc Lưu Liên Kết dưới dạng):L11_ch3_h89.cg3
Xem trực tiếp hình vẽ động trên màn hình.
 5 5
Chứng minh rằng 1) Nếu có 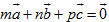 và một trong ba số m, n, p khác không thì ba vectơ và một trong ba số m, n, p khác không thì ba vectơ 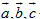 đồng phẳng; đồng phẳng; 2) Nếu 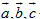 là ba vectơ không đồng phẳng và là ba vectơ không đồng phẳng và 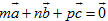 thì m = n = p = 0. thì m = n = p = 0. Bài toán 2 Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy các điểm P, Q lần lượt thuộc các đường thẳng AD và BC sao cho 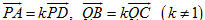 . Chứng minh rằng các điểm M, N, P, Q cùng thuộc một mặt phẳng (h.90). . Chứng minh rằng các điểm M, N, P, Q cùng thuộc một mặt phẳng (h.90). 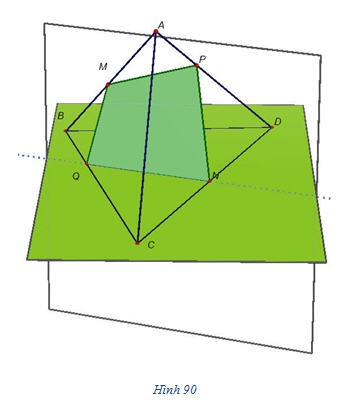
Tải trực tiếp tệp hình học động (Nhấn chuột phải vào liên kết rồi chọn Save As hoặc Lưu Liên Kết dưới dạng):L11_ch3_h90.cg3
Xem trực tiếp hình vẽ động trên màn hình.
 6 (Để giải bài toán 2) 6 (Để giải bài toán 2)
1) Từ hệ thức 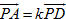 hãy chứng tỏ hãy chứng tỏ 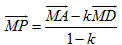
Tương tự, ta cũng có 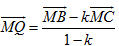
2) Từ hai đẳng thức trên, chứng minh rằng 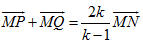
Vậy các điểm M, N, P cùng thuộc một mặt phẳng. Định lí 1 nói đến điều kiện để có thể biểu thị một vectơ qua hai vectơ không cùng phương. Định lí dưới đây sẽ nói về biểu thị một vectơ qua ba vectơ không đồng phẳng. ĐỊNH LÍ 2 
Chứng minh 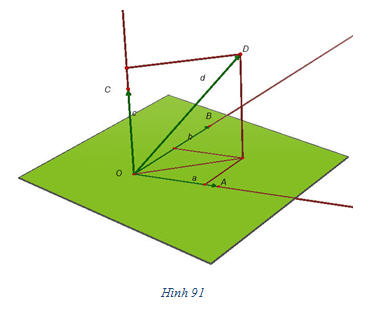
Tải trực tiếp tệp hình học động (Nhấn chuột phải vào liên kết rồi chọn Save As hoặc Lưu Liên Kết dưới dạng):L11_ch3_h91.cg3
Xem trực tiếp hình vẽ động trên màn hình.
Từ điểm O, ta đặt 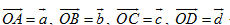 thì không cùng thuộc một mặt phẳng. thì không cùng thuộc một mặt phẳng. Từ điểm D kẻ đường thẳng song song (hoặc trùng) với đường thẳng OC, cắt mặt phẳng (OAB) tại điểm D’ (h.91). Khi đó 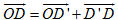
Theo định lí 1, ta có các số m, n sao cho 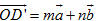 . Ngoài ra do . Ngoài ra do 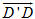 và và 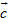 cùng phương nên có số p để cùng phương nên có số p để 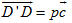 . Vậy . Vậy 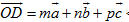 . . Giả sử còn có 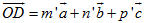 thì thì 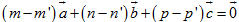
Vì 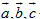 không đồng phẳng nên m - m’ = n - n’ = p - p’ = 0 hay m = m’, n = n’, p = p’. không đồng phẳng nên m - m’ = n - n’ = p - p’ = 0 hay m = m’, n = n’, p = p’. Suy ra các số m, n, p là duy nhất. Bài toán 3 Cho hình hộp ABCD.A’B’C’D’. Xét các điểm M và N lần lượt thuộc các đường thẳng A’C và C’D sao cho 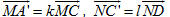 ( k và l đều khác 1). ( k và l đều khác 1). Đặt: 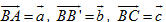
a) Hãy biểu thị các vectơ 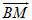 và và 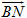 qua các vectơ qua các vectơ 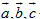 . . b) Xác định các số k, l để đường thẳng MN song song với đường thẳng BD’. Giải (h.92) 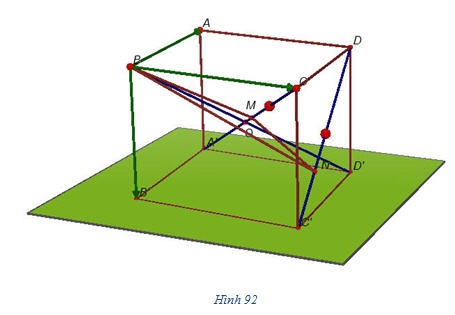
Tải trực tiếp tệp hình học động (Nhấn chuột phải vào liên kết rồi chọn Save As hoặc Lưu Liên Kết dưới dạng):L11_ch3_h92.cg3
Xem trực tiếp hình vẽ động trên màn hình.
a) Từ giả thiết ta có: 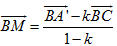
do đó: 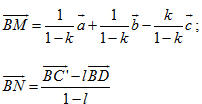
do đó: 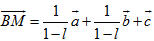
b) Vì BD’ và C’D là hai đường thẳng chéo nhau và N thuộc đường thẳng C’D nên đường thẳng MN không thể trùng với đường thẳng BD’. Vậy đường thẳng MN song song với đường thẳng BD’ khi và chỉ khi 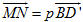 Do 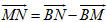 nên ta có nên ta có 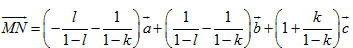
Mặt khác 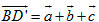 (quy tắc hình hộp) mà (quy tắc hình hộp) mà 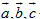 là ba vectơ không đồng phẳng nên là ba vectơ không đồng phẳng nên 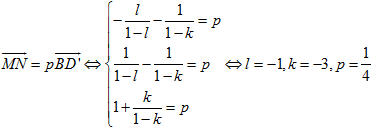
Vậy khi k = -3, l = -1 thì đường thẳng MN và đường thẳng BD’ song song với nhau.
Câu hỏi và bài tập
1. Ba vectơ 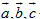 có đồng phẳng không nếu một trong hai điều sau đây xảy ra? có đồng phẳng không nếu một trong hai điều sau đây xảy ra? a) Có một vectơ trong ba vectơ đó bằng 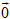 . . b) Có hai vectơ trong ba vectơ đó cùng phương. 2. Cho hình chóp S.ABCD. a) Chứng minh rằng nếu ABCD là hình bình hành thì 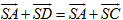 . Điều ngược lại có đúng không? . Điều ngược lại có đúng không? b) Gọi O là giao điểm của AC và BD. Chứng tỏ rằng ABCD là hình bình hành khi và chỉ khi 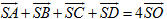 . . 3. Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của hai đường thẳng AB’ và A’B. Chứng minh rằng các đường thẳng GI và CG’ song song với nhau. 4. Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của CD và DD’ ; G và G’ lần lượt là trọng tâm của các tứ diện A’D’MN và BCC’D’. Chứng minh rằng đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau. 5. Trong không gian cho tam giác ABC. a) Chứng minh rằng nếu điểm M thuộc mp(ABC) thì có ba số x, y, z mà x + y + z = 1 sao cho 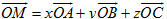 với mọi điểm O. với mọi điểm O. b) Ngược lại, nếu có một điểm O trong không gian sao cho 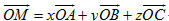 , trong đó x + y + z = 1 thì điểm M thuộc mp(ABC ). , trong đó x + y + z = 1 thì điểm M thuộc mp(ABC ). 6. Cho hình chóp S.ABC. Lấy các điểm A’, B’, C’ lần lượt thuộc các tia SA, SB, SC sao cho SA = aSA’, SB = bSB’, SC = cSC’, trong đó a, b, c là các số thay đổi. Chứng minh rằng mặt phẳng ( A’B’C’ ) đi qua trọng tâm của tam giác ABC khi và chỉ khi a + b + c = 3.
School@net
|

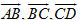 không cùng nằm trong một mặt phẳng nào cả (h.82).
không cùng nằm trong một mặt phẳng nào cả (h.82).

 và kiểm tra tính đúng đắn của đẳng thức
và kiểm tra tính đúng đắn của đẳng thức 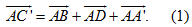
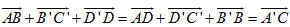
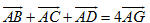 có đúng không?
có đúng không?
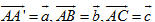 (h.85).
(h.85).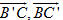 qua các vectơ
qua các vectơ 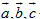 .
.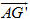 qua
qua 
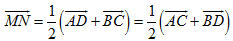
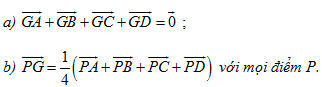

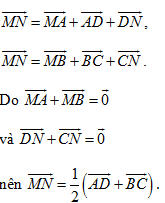
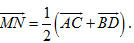
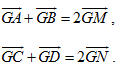
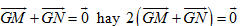
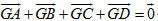
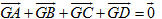
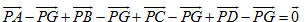
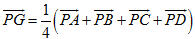
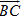 và
và 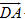 .
.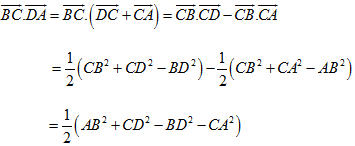
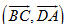 xác định bởi
xác định bởi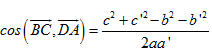
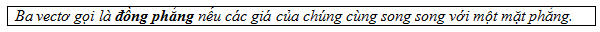

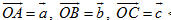 thì ba vectơ
thì ba vectơ 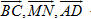 đồng phẳng.
đồng phẳng.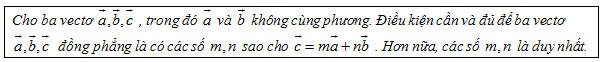

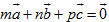 và một trong ba số m, n, p khác không thì ba vectơ
và một trong ba số m, n, p khác không thì ba vectơ 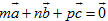 thì m = n = p = 0.
thì m = n = p = 0.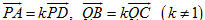 . Chứng minh rằng các điểm M, N, P, Q cùng thuộc một mặt phẳng (h.90).
. Chứng minh rằng các điểm M, N, P, Q cùng thuộc một mặt phẳng (h.90).
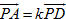 hãy chứng tỏ
hãy chứng tỏ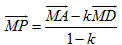
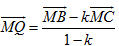
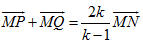


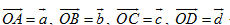 thì không cùng thuộc một mặt phẳng.
thì không cùng thuộc một mặt phẳng.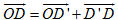
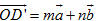 . Ngoài ra do
. Ngoài ra do 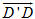 và
và 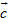 cùng phương nên có số p để
cùng phương nên có số p để 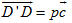 . Vậy
. Vậy 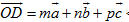 .
.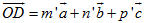 thì
thì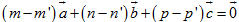
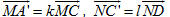 ( k và l đều khác 1).
( k và l đều khác 1).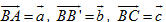
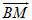 và
và 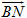 qua các vectơ
qua các vectơ 
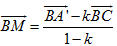
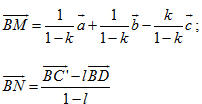
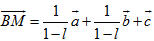
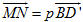
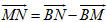 nên ta có
nên ta có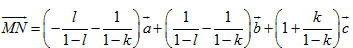
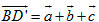 (quy tắc hình hộp) mà
(quy tắc hình hộp) mà 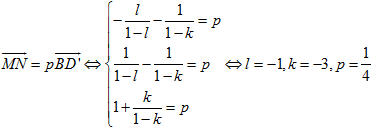
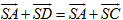 . Điều ngược lại có đúng không?
. Điều ngược lại có đúng không?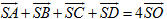 .
.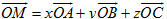 với mọi điểm O.
với mọi điểm O.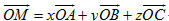 , trong đó x + y + z = 1 thì điểm M thuộc mp(ABC ).
, trong đó x + y + z = 1 thì điểm M thuộc mp(ABC ).




