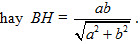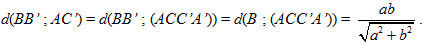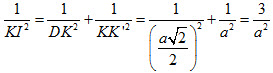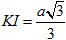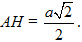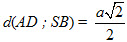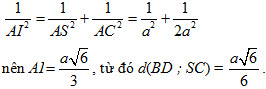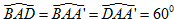Trên hình 125a), ta có H là hình chiếu của M trên mp(P) và trên hình 125b), ta có H là hình chiếu của M trên đường thẳng ∆.
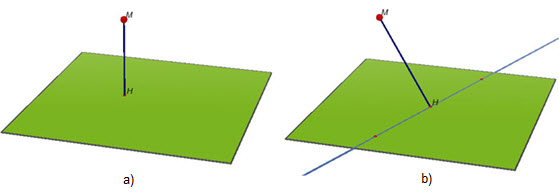
Hình 125
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_Ch3_h125.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Ta có định nghĩa sau: ĐỊNH NGHĨA 1 Khoảng cách từ điểm M đến mặt phẳng (P) (hoặc đến đường thẳng ∆) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên mặt phẳng (P) (hoặc trên đường thẳng ∆). |
Khoảng cách từ điểm M đến mặt phẳng (P) được kí hiệu là d(M ; (P)). Khoảng cách từ điểm M đến đường thẳng ∆được kí hiệu là d(M ; (P)).  1. Trong các khoảng cách từ M đến một điểm bất kì thuộc mặt phẳng (P), khoảng cách nào là nhỏ nhất? 1. Trong các khoảng cách từ M đến một điểm bất kì thuộc mặt phẳng (P), khoảng cách nào là nhỏ nhất?
 2. Cùng câu hỏi như trên nếu thay mặt phẳng (P) bởi đường thẳng ∆. 2. Cùng câu hỏi như trên nếu thay mặt phẳng (P) bởi đường thẳng ∆.
2. Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song Cho đường thẳng a song song với mặt phẳng (P). Với hai điểm A, B bất kì trên a, hiển nhiên ta có d(A ; (P)) = d(B ; (P))(h.126). Như vậy, d(A ; (P)) không phụ thuộc vào vị trí của điểm A khi A thay đổi trên a. Từ đó ta có định nghĩa
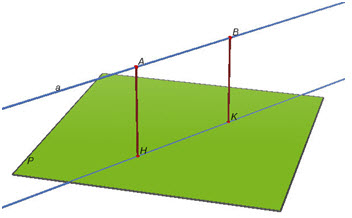
Hình 126
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_Ch3_h126.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
ĐỊNH NGHĨA 2 Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm nào đó của a đến mặt phẳng (P). |
Kí hiệu khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với nó là d(a ; (P)).
 3. Khi đường thẳng a song song với mặt phẳng (P), trong các khoảng cách từ một điểm bất kì của a đến một điểm bất kì của (P), khoảng cách nào là nhỏ nhất? 3. Khi đường thẳng a song song với mặt phẳng (P), trong các khoảng cách từ một điểm bất kì của a đến một điểm bất kì của (P), khoảng cách nào là nhỏ nhất?
Cho hai mặt phẳng song song (P) và (Q). Khi ấy, dễ thấy d(A ; (Q)) = d(B ; (Q)) với A, B là hai điểm bất kì thuộc (P), tức là d(A ; (Q)) không phụ thuộc vào vị trí của điểm A khi a thay đổi trên (P)(h.127).
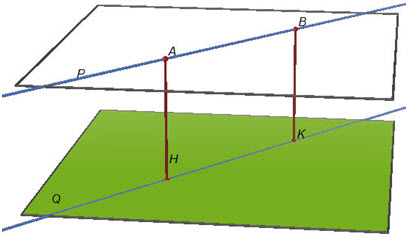
Hình 127
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_Ch3_h127.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Từ đó ta có định nghĩa ĐỊNH NGHĨA 3 Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia. |
Ki hiệu khoảng cách giữa hai mặt phẳng song song (P) và (Q) là d((P) ; (Q)) thì d((P) ; (Q)) = d((A ; (Q)) = d(C ; (P)), trong đó A là một điểm nào đó thuộc (P) và C là một điểm nào đó thuộc (Q).  4. Trong các khoảng cách giữa hai điểm bất kì lần lượt thuộc hai mặt phẳng song song, khoảng cách nào là nhỏ nhất? 4. Trong các khoảng cách giữa hai điểm bất kì lần lượt thuộc hai mặt phẳng song song, khoảng cách nào là nhỏ nhất?
3. Khoảng cách giữa hai đường thẳng chéo nhau Bài toán Cho hai đường thẳng chéo nhau a và b. Tìm đường thẳng c cắt cả a và b đồng thời vuông góc với cả a và b. Giải Do a và b chéo nhau nên có duy nhất mặt phẳng (Q) chứa đường thẳng b và song song với đường thẳng a.
Mặt phẳng (P) đi qua a và vuông góc với (Q) cắt đường thẳng b tại điểm J. Gọi c là đường thẳng đi qua J và vuông góc với (Q) thì c nằm trong mp(P), do đó c cắt a tại điểm I. Khi ấy c là đường thẳng phải tìm (h.128).
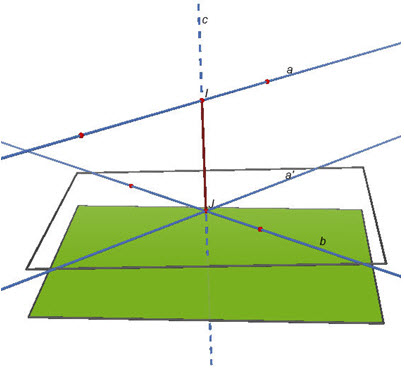
Hình 128
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_Ch3_h128.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
 Chứng minh tính duy nhất của đường thẳng c trong bài toán trên. Chứng minh tính duy nhất của đường thẳng c trong bài toán trên.
Thuật ngữ Đường thẳng c nói trên gọi là đường vuông góc chung của hai đường thẳng chéo nhau a và b. Nếu đường vuông góc chung cắt hai đường thẳng chéo nhau tại I và J thì đoạn thẳng IJ gọi là đoạn thẳng góc chung của hai đường thẳng đó (h.129).
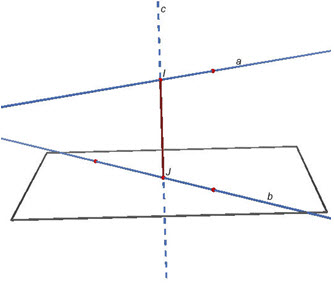
Hình 129
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_Ch3_h129.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
ĐỊNH NGHĨA 4 Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó. |
 5. Trong các khoảng cách giữa hai điểm bất kì lần lượt nằm trên hai đường thẳng chéo nhau, khoảng cách nào là nhỏ nhất? 5. Trong các khoảng cách giữa hai điểm bất kì lần lượt nằm trên hai đường thẳng chéo nhau, khoảng cách nào là nhỏ nhất?
Nếu gọi (P) và (Q) là hai mặt phẳng song song với nhau lần lượt đi qua hai đường thẳng a và b thì rõ ràng: IJ = d(a ; (Q)) = d(b ; (P)) = d((P) ; (Q))(h.130).
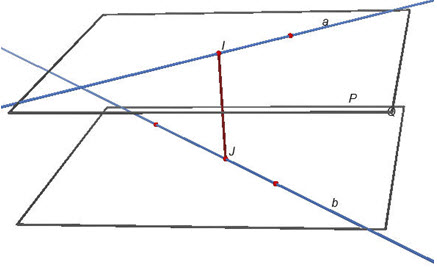
Hình 130
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_Ch3_h130.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Vậy ta có: Nhận xét 1) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó và mặt phẳng song song với nó, chứa đường thẳng còn lại. 2) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
4. Một số ví dụ Ví dụ 1 Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, AD = b, AA’ = c. a) Tính khoảng cách từ điểm B đến mặt phẳng (ACC’A’). b) Tính khoảng cách giữa hai đường thẳng BB’ và AC’. c) Tính khoảng cách giữa hai mặt phẳng (AB’C) và (A’C’D) trong trường hợp a = b= c. Giải(h.131)
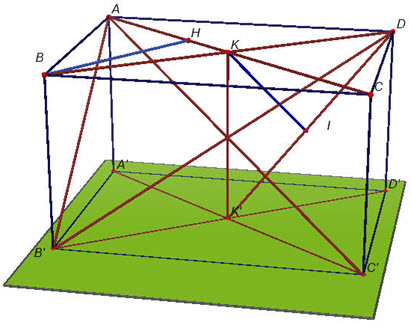
Hình 131
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_Ch3_h131.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
a) Kẻ BH vuông góc với AC, do BH⊥AA’nên BH⊥ (ACC’A’). Vậy d(B ; (ACC’A’)) = BH. Ta có BH . AC = BA . BC 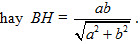
b) BB’ và AC’ chéo nhau mà BB’ // (ACC’A’) nên 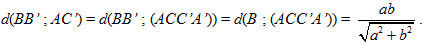
c) Dễ thấy mp(AB’C) và mp(A’C’D’) song song với nhau. Do a = b = c nên ABCD.A’B’C’D’là hình lập phương. Khi đó, gọi K và K’ lần lượt là tâm của hai hình vuông ABCD và A’B’C’D’ thì mp(KK’D’D) vuông góc với mp(DA’C’). Kẻ KI vuông góc với giao tuyến DK’ của hai mặt phẳng đó thì KI mp(A’C’D). Vậy khoảng cách giữa hai mặt phẳng (AB’C) và (A’C’D) bằng KI. Ta có tam giác KK’D vuông tại K nên
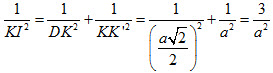
tức là 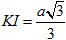 Chú ý rằng BD’ vuông góc với hai mặt phẳng (ACB’), (DA’C’) và đi qua tâm G, G’ của hai tam giác đều AB’C, DA’C’. Từ đó suy ra khoảng cách cần tìm cũng bằng GG’ và bằng  BD’. BD’.
Ví dụ 2 Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA⊥ (ABCD) và SA = a. Tính khoảng cách giữa hai đường thẳng a) SB và AD; b) BD và SC. Giải (h.132)
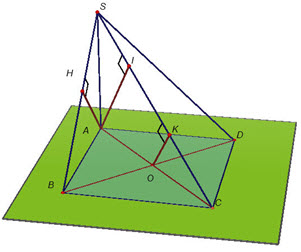
Hình 132
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_Ch3_h132.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
a) Ta có AD⊥ (SBA), kẻ AH vuông góc với SB thì AH là đường vuông góc chung của SB và AD. Vậy d(AD ; SB) = AH. Vì AHlà đường cao của tam giác vuông cân SAB nên 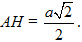
Từ đó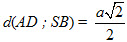 . . b) Ta có BD vuông góc với mp(SAC) tại tâm O của hình vuông ABCD. Trong mp(SAC), kẻ OK vuông góc với SC thì OKlà đường vuông góc chung của BD và SC. Dễ thấy d(BD ; SC) = OK =  AI (AI là đường cao của tam giác vuông SAC). Ta có AI (AI là đường cao của tam giác vuông SAC). Ta có 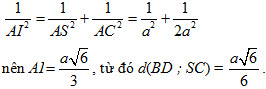
Câu hỏi và bài tập 29. Cho tứ diện ABCD có AC = BC = AD = BD = a, AB = c, CD = c’. Tính khoảng cách giữa hai đường thẳng AB và CD. 30. Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 300. Hình chiếu H của điểm A trên mặt phẳng (A’B’C’) thuộc đường thẳng B’C’. a) Tính khoảng cách giữa hai mặt phẳng đáy. b) Chứng minh rằng hai đường thẳng AA’ và B’C’ vuông góc, tính khoảng cách giữa chúng. 31. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BC’ và CD’. 32. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = AA’ = a, AC’ = 2a. a) Tính khoảng cách từ điểm D đến mặt phẳng (ACD’). b) Tìm đường vuông góc chung của các đường thẳng AC’ và CD’. Tính khoảng cách giữa hai đường thẳng ấy. 33. Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và 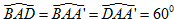 . Tính khoảng cách giữa hai mặt đáy (ABCD) và (A’B’C’D’). . Tính khoảng cách giữa hai mặt đáy (ABCD) và (A’B’C’D’). 34. Cho hình chóp S.ABCD có đáy là hình chữ nhật và AB = 2a, BC = a. Các cạnh bên của hình chóp bằng nhau và bằng 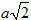 . . a) Tính khoảng cách từ S đến mặt phẳng đáy (ABCD). b) Gọi E và F lần lượt là trung điểm của các cạnh AB và CD; K là điểm bất kì thuộc đường thẳng AD. Chứng minh rằng khoảng cách giữa hai đường thẳng EF và SK không phụ thuộc vào K, hãy tính khoảng cách đó theo a.
School@net
|






 Chứng minh tính duy nhất của đường thẳng c trong bài toán trên.
Chứng minh tính duy nhất của đường thẳng c trong bài toán trên.