Qua phép biến hình F, mỗi hình 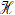 được biến thành hình được biến thành hình 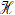 ’ gồm tất cả các ảnh của các điểm thuộc hình ’ gồm tất cả các ảnh của các điểm thuộc hình 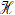 . .
Sau đây ta xét phép đối xứng qua mặt phẳng, đó là một phép biến hình thường gặp.
1. Phép đối xứng qua mặt phẳng
ĐỊNH NGHĨA 1 (h.7)
Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính nó và biến mỗi điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực của đoạn thẳng MM’.
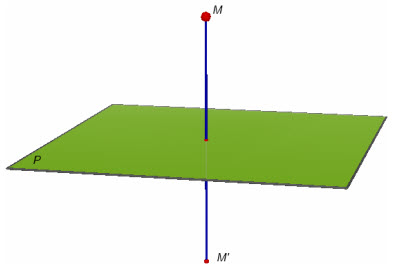
Hình 7
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch1_h7.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
ĐỊNH LÝ 1 (h.8) Nếu phép đối xứng qua mp(P) biến hai điểm M, N lần lượt thành hai điển M’, N’ thì M’N’= MN. (Như vậy có thể nói : phép đối xứng qua mặt phẳng là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì).
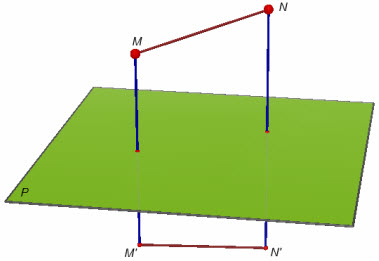
Hình 8
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch1_h8.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
1 (để chứng minh định lí 1)
Nếu M, N nằn trên (P) thì M’ và N’ trùng M và N’ trùng N nên M’N’=MN. Nếu có ít nhất một trong hai điểm M, N không nằm trên (P) thì có mp(Q) đi qua các điểm M, N, M’, N’. Hãy dùng kiến thức hình học phẳng để chứng minh M’N’=MN.
Khi đứng trước một tấm gương phẳng, mỗi người sẽ nhìn thấy hình của mình ở “phía sau” tấm gương đó (h.9). Phép đối xứng qua mặt phẳng của tấm gương đã “biến” mỗi người thành hình của họ.

Hình 9. Ảnh chụp một em bé trước gương
Tải trực tiếp tệp hình học động: L11_nc_Ch3_h134.ggb Xem trực tiếp hình vẽ động trên màn hình.
Hình 10 là ảnh của Tháp Rùa đang soi bóng trên mặt nước Hồ Gươm (Hà Nội). Mặt hồ xem như là một phần của mặt phẳng, phép đối xứng qua mặt phẳng đó biến Tháp Rùa thành cái bóng của nó.

Hình 10. Ảnh chụp Tháp Rùa và bóng của nó
Tải trực tiếp tệp hình học động: L11_nc_Ch3_h134.ggb Xem trực tiếp hình vẽ động trên màn hình.
2. Mặt phẳng đối xứng của một hình
ĐỊNH NGHĨA 2
Nếu phép đối xứng qua mặt phẳng (P) biến hình 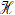 thành chính nó thì (P) gọi là mặt phẳng đối xứng của hình thành chính nó thì (P) gọi là mặt phẳng đối xứng của hình 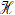 . .
Một số ví dụ
Ví dụ 1
Mọi mặt phẳng đi qua tâm của mặt cầu đều là mặt phẳng đối xứng của mặt cầu (h.11).
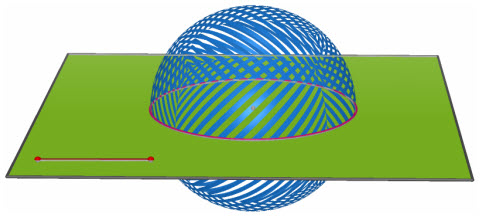
Hình 11
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch1_h11.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Ví dụ 2
Cho tứ diện đều ABCD (h.12). Gọi M là trung điểm của cạnh CD thì phép đối xứng qua mp(ABM) biến A thành A, B thành B, C thành D, D thành C. Như vậy, phép đối xứng đó biến tứ diện ABCD thành chính nó, suy ra mặt phẳng (ABM) thành mặt phẳng đối xứng của tứ diện ABCD. Hình tứ diện đều ABCD có sáu mặt phẳng đối xứng. Đó là các mặt phẳng đi qua một cạnh và trung điểm của cạnh đối diện.
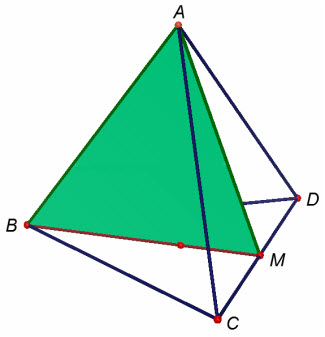
Hình 12
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch1_h12.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Ví dụ 3
Xét hình lập phương ABCD.A’B’C’D’ (h.13).
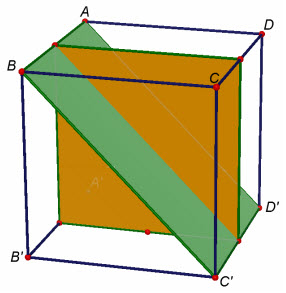
Hình 13
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch1_h13.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Nếu (P) là mặt phẳng trung trực của cạnh AB thì nó cũng là mặt phẳng trung trực của cạnh AB thì nó cũng là mặt phẳng trung trực của các cạnh CD, A’B’ và C’D’, bởi vậy nó là mặt phẳng đối xứng của hình lập phương. Tương tự, các mặt phẳng trung trực của các cạnh AD, và AA’ cũng là những mặt phẳng đối xứng của hình lập phương.
Gọi (Q) là mặt phẳng đi qua hai cạnh đối diện AB và C’D’ thì (Q) là mặt phẳng đối xứng của hình lập phương vì phép đối xứng qua (Q) biến mỗi điểm A, B, C’, D’ thành chính nó và biến điểm A’ thành D, D thành A’,C thành B’và B’ thành C.
?1 Như vậy hình lập phương có bao nhiêu mặt phẳngđối xứng ?
3. Hình bát diện đều và mặt phẳng đối xứng của nó
Hình 14 là một hình đa diện có 8 mặt là các tam giác đều : EAB, EBC, ECD, EDA, FAB, FBC, FCD và FDA, có 6 đỉnh A, B, C, D, E, F, mỗi đỉnh là đỉnh chung cho 4 tam giácđều. Hình đó gọi là hình bát diện đều (hay hình tám mặt đều) và được kí hiệu là ABCDEF.
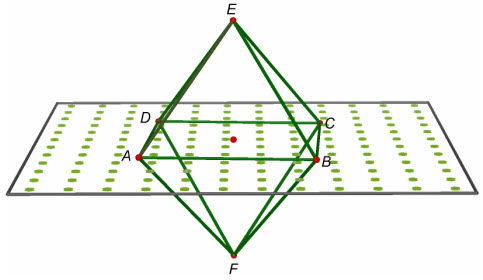
Hình 14
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch1_h14.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Tính chất
Bốn đỉnh A, B, C, D nằm trên một mặt phẳng và đó là một mặt phẳng đối xứng của hình bát diện đều ABCDEF.
Chứng minh
Vì mỗi điểm A, B, C, D cách đều hai điểm E và F nên chúng nằm trên mặt phẳng trung trực của đoạn thẳng EF. Phép đối xứng qua mặt phẳng đó biến mỗi điểm A, B, C, D thành chính nó và biến điểm E thành F, F thành E nên mp(ABCD) là mặt phẳng đối xứng của bát diện đều ABCDEF.¢
2 Tìm thêm các mặt phẳng đối xứng khác của hình bát diện đều.
4. Phép dời hình và sự bằng nhau của các hình
Phép dời hình trong không gian được định nghĩa tương tự như trong mặt phẳng.
Định nghĩa phép dời hình
Một phép biến hình F trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm bất kì (có nghĩa là nếu F biến hai điểm bất kì M, N lần lượt thành hai điểm M’, N’ thì M’N’=MN).
Từ định nghĩa đó, ta suy ra phép dời hình biến đường thẳng thành đường thẳng, mặt phẳng thành mặt phẳng,… .
Hiển nhiên phép đối xứng qua mặt phẳng là một phép dời hình. Phép đồng nhất (biến mỗi điểm thành chính nó) là một phép dời hình.
Rõ ràng nếu thực hiện liên tiếp các phép dời hình thì ta cũng có kết quả là phép dời hình. Nói cách khác : Hợp thành của những phép dời hình là phép dời hình.
Một số ví dụ về phép dời hình
Ngoài phép đối xứng quanh mặt phẳng, ta thường gặp một số phép dời hình sau đây :
• Phép tịnh tiến : Phép tịnh tiến theo vectơ 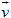 là phép biến hình biến mỗi điểm M thành điểm M’ sao cho là phép biến hình biến mỗi điểm M thành điểm M’ sao cho 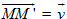 . .
• Phép đối xứng qua đường thẳng (còn gọi là phép đối xứng trục) : cho đường thẳng d, phép đối xứng qua đường thẳng d là phép biến hình biến mỗi điểm thuộc d thành chính nó và biến mỗi điểm M không thuộc d thành điểm M’sao cho trong mặt phẳng (M, d), d là đường trung trực của đoạn thẳng MM’.
• Phép đối xứng qua một điểm (còn gọi là phép đối xứng tâm) : Cho điểm O, phép đối xứng qua điểm O là phép biến hình biến mỗi điểm Mthành điểm M’ sao cho 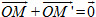 . .
Định nghĩa hai hình bằng nhau
Hai hình 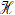 và và 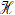 ’ gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia. ’ gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
?2 Hai mặt cầu có bán kính bằng nhau thì có bằng nhau hay không ? Vì sao ?
Ví dụ 4. Cho hình chóp tam giác đều S.ABC. Gọi A’, B’, C’ lần lượt là trung điểm của cạnh BC, CA và AB. Khi đó hai tứ diện SABA’ và SBCB’ bằng nhau.
Giải (h.15)
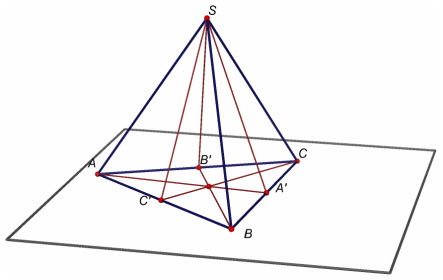
Hình 15
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch1_h15.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Thật vậy, phép đối xứng qua mp(SAA’) biến các điểm S, A, B, A’ lần lượt thành các điểm S, A, C, A’ và phép đối xứng qua mp(SCC’) biến các điểm S, A, C, A’ lần lượt thành các điểm S, B, C, B’. Như vậy, qua hai phép đối xứng trên, bốn đỉnh S, A, B, A’ của tứ diện SABA’ biến thành bốn đỉnh S, B, C, B’ của tứ diện SBCB’ nêu theo định nghĩa, hai tứ diện đó bằng nhau. ¢
ĐỊNH LÍ 2
Hai hình tứ diện ABCD và A’B’C’D’ bằng nhau nếu chúng có các cạnh tương ứng bằng nhau, nghĩa là AB=A’B’, BC=B’C’, CD=C’D’, AC=A’C’, BD=B’D’.
Chứng minh. Ta xét các trường hợp sau :
Trường hợp 1 (h.16). Hai hình tứ diện có ba cặp đỉnh tương ứng trùng nhau, chẳng hạn A trùng A’, B trùng B’, C trùng C’, D khác D’.
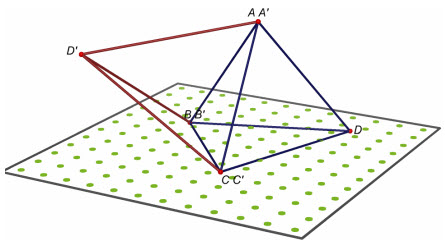
Hình 16
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch1_h16.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Khi đó, mỗi điểm A, B, C cách đều hai điểm D và D’ trên mp(ABC) là mặt phẳng trung trực của đoạn thẳng DD’, suy ra phép đối xứng qua mp(ABC) biến các đỉnh A, B, C, D lần lượt thành các đỉnh A’, B’, C’, D’. Vậy hai tứ diện ABCD và A’B’C’D’bằng nhau.
Trường hợp 2 (h.17). Hai hình tứ diện đó có hai cặp đỉnh tương ứng trùng nhau, chẳng hạn A trùng A’, B trùng B’.
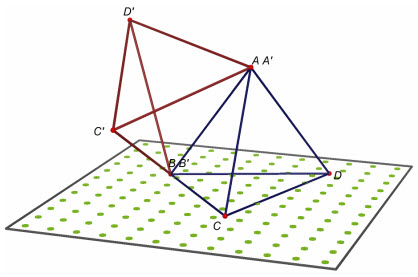
Hình 17
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch1_h17.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Khi đó gọi (P) là mặt phẳng trung trực của đoạn thẳng CC’ thì (P) đi qua A và B (vì A và B cùng cách đều hai điểm C và C’). Vậy phép đối xứng qua mp(P) sẽ biến cá điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D1 và do đó tứ diện ABCD bằng tứ diện A’B’C’D1.
Vì hai tứ diện A’B’C’D1 và A’B’C’D’ có các cạnh tương ứng bằng nhau và có ba đỉnh tương ứng trùng nhau nên theo trường hợp 1, chúng bằng nhau.
Trường hợp 3. Hai hình tứ diện có một cặp đỉnh tương ứng trùng nhau, chẳng hạn A trùng A’.
Khi đó, gọi (Q) là mặt phẳng trung trực của BB’ thì (Q) đi qua A (vì A cách đều B và B’). Vậy phép đối xứng qua (Q) biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C1, D1 và do đó, hai tứ diện ABCD và A’B’C1D1 bằng nhau. Mặt khác, hai tứ diện A’B’C1D1 và A’B’C’D’ có các cạnh tương ứng bằng nhau và có hai cặp đỉnh tương ứng trùng nhau nên theo trường hợp 2, chúng bằng nhau.
Trường hợp 4. Hai hình tứ diện đó không có cặp đỉnh tương ứng nào trùng nhau.
Khi đó gọi (R) là mặt phẳng trung trực của AA’, phép đối xứng qua (R) biến các điểm A, B, C, D lần lượt thành các điểm A’, B1, C1, D1 nên tứ diện ABCD bằng tứ diện A’B1C1D1 : mà hai tứ diện A’B1C1D1 và A’B’C’D’ có cạnh tương ứng bằng nhau và một cặp đỉnh tương ứng trùng nhau, do đó chúng bằng nhau theo trường hợp 3. ¢
HỆ QUẢ 1
Hai tứ diện đều có cạnh bằng nhau thì bằng nhau.
HỆ QUẢ 2 Hai hình lập phương có cạnh bằng nhau thì bằng nhau.
Chứng minh (h.18)
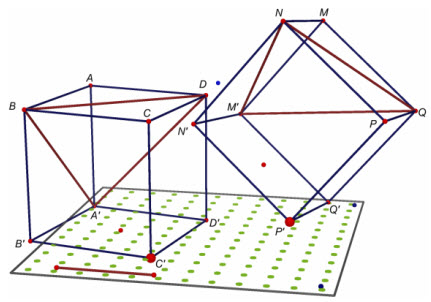
Hình 18
Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch1_h18.cg3
Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Giả sử ABCD. A’B’C’D’ và MNPQ.M’N’P’Q’ là hai hình lập phương có cạnh đều bằng a. Hai tứ diện ABDA’ và MNQM’ có các cạnh tương ứng bằng nhau nên bằng nhau, tức là có phép dời hình F biến các điểm A, B, D, A’ lần lượt thành M, N, Q, M’. Vì F là phép dời hình nên F biến hình vuông thành hình vuông, do đó F biến các điểm Cthành điểm P , biến điểm B’ thành N’, biến điểm D’ thành Q’ và biến các điểm C’ thành P’. Như vậy, hai hình lập phương đã cho bằng nhau. ¢
Câu hỏi và bài tập
6. Gọi Đ là phép đối xứng qua mặt phẳng (P) và a là một đường thẳng nào đó. Giả sử Đ biến đổi đường thẳng a thành đường thẳng a’. Trong trường hợp nào thì : a) a trùng với a’ ; b) a song song a’ ; c) a cắt a’ ; d) a và a’ chéo nhau ?
7. Tìm các mặt phẳng đối xứng của các hình sau đây :
a) Hình chóp tứ giác đều ; b) Hình chóp cụt tam giác đều ; c) Hình hộp chữ nhật mà không có mặt nào là hình vuông.
8. Cho hình lập phương ABCD. A’B’C’D’. Chứng minh rằng :
a) Các hình chóp A. A’B’C’D’ và C’.ABCD bằng nhau. b) Các hình lăng trụ ABC.A’B’C’ và AA’D’.BB’C’ bằng nhau.
9. Chứng minh rằng các phép tịnh tiến, đối xứng trục, đối xứng tâm là những phép dời hình.
10. Chứng minh rằng :
a) Hợp thành của hai phép đối xứng qua hai mặt phẳng song song (P) và (Q) là một phép tịnh tiến ; b) Hợp thành của hai phéo đối xứng qua hai mặt phẳng (P) và (Q)vuông góc với nhau là một phép đối xứng qua đường thẳng.
School@net
|

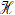 được biến thành hình
được biến thành hình 







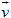 là phép biến hình biến mỗi điểm M thành điểm M’ sao cho
là phép biến hình biến mỗi điểm M thành điểm M’ sao cho 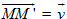 .
.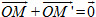 .
.








