Như vậy, phép vị tự trong không gian được định nghĩa hoàn toàn tương tự như trong mặt phẳng. Các tính chất sau đây của phép vị tự đều có thể được chứng minh tương tự như trong mặt phẳng. Các tính chất cơ bản của phép vị tự 1. Nếu phép vị tự tỉ số k biến hai điểm M, N thành hai điểm M’, N’ thì 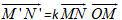 , và do đó M’N’= MN. , và do đó M’N’= MN. 2. Phép vị tự biến ba điểm thẳng hàng thành bà điểm thẳng hàng, bốn điểm đồng phẳng thành bốn điểm đồng phẳng. Từ đó suy ra phép vị tự biến đường thẳng thành đường thẳng, mặt phẳng thành mặt phẳng… Ví dụ 1 Cho hình tứ diện ABCD. Gọi A’, B’, C’, D’ lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Chứng minh rằng có phép vị tự biến tứ diện ABCD thành tứ diện A’B’C’D’. Giải (h.19) 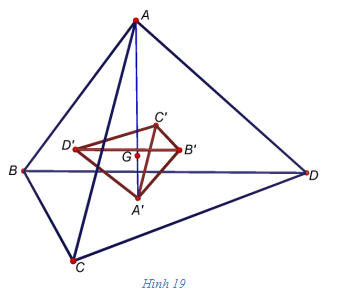
Tải trực tiếp tệp hình học động (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h19.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Gọi G là trọng tâm của tứ diện ABCD. Khi đó ta biết rằng : 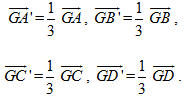
Suy ra phép vị tự V tâm G, tỉ số k = - 1/3 biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’. Vậy V biến tứ diện ABCD thành tứ diện A’B’C’D’. ?1 Trong trường hợp nào thì phép vị tự là một phéo dời hình ? 2. Hai hình đồng dạng ĐỊNH NGHĨA 2 Hình H được gọi là đồng dạng với hình H’ H thành hình H1 mà hình H1 bằng hình H’. Ví dụ 2. Chứng minh rằng hai hình tứ diện đều bất kì luôn luôn đồng dạng với nhau. Chứng minh (h.20) 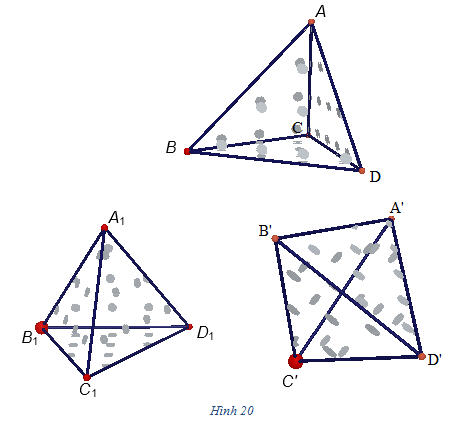
Tải trực tiếp tệp hình học động 20 (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h20.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Tải trực tiếp tệp hình học động 20a(Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h20a.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Giả sử ABCD là tứ diện đều có cạnh bằng a và A’B’C’D’ là tứ diện đều có cạnh bằng a’. Ta xét phép vị tự V có tân O tùy ý và có tỉ số  . Khi đó dễ thấy tứ diện đều ABCD biến thành tứ diện đều A1B1C1D1 có cạnh bằng a’. Vậy tứ diện A1B1C1D1 bằng tứ diện A’B’C’D’. Theo định nghĩa, tứ diện ABCD đồng dạng với tứ diện A’B’C’D’. . Khi đó dễ thấy tứ diện đều ABCD biến thành tứ diện đều A1B1C1D1 có cạnh bằng a’. Vậy tứ diện A1B1C1D1 bằng tứ diện A’B’C’D’. Theo định nghĩa, tứ diện ABCD đồng dạng với tứ diện A’B’C’D’. Ví dụ 3. Chứng minh rằng hai hình lập phương bất kì đều đồng dạng với nhau. Chứng minh tương tự ở Ví dụ 2. 3. Khối đa diện đều và sự đồng dạng của các khối đa diện đều Trước hết ta nói về khối đa diện lồi, một khái niệm tương tự như khái niệm đa giác lồi trong hình học phẳng. Một khối đa diện được gọi là khối đa diện lồi nếu với bất kì hai điểm A và B nào của nó thì mọi điểm của đoạn thẳng AB cũng thuộc khối đó. Các khối đa diện trên hình 21 không phải là những khối đa diện lồi. 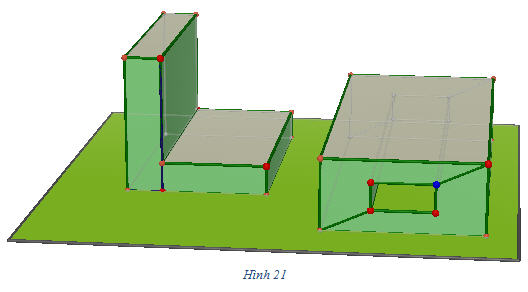
Tải trực tiếp tệp hình học động (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h21.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) ?2 Tại sao các khối đa diện trên hình 21 không phải là những khối đa diện lồi ? Chúng ta đã biết thế nào là đa giác đều. Bây giờ ta sẽ định nghĩa thế nào là khối đa diện đều. ĐỊNH NGHĨA 3 Khối đa diện đều là một khối đa diện lồi có hai tính chất sau đây : a) Các mặt là những đa giác đều và có cùng số cạnh ; b) Mỗi đỉnh là đỉnh chung của cùng một số cạnh. Khối đa diện đều mà mỗi mặt là đa giác đều n cạnh và mỗi đỉnh là đỉnh chung của p cạnh được gọi là khối đa diện đều loại {n ; p}. ?3 Khối tứ diện đều, khối bát diện đều và khối lập phương là những khối đa diện đều thuộc loại gì ? Ngoài khối tứ diện đều, khối lập phương và khối bát diện đều, hình 22 dưới đây cho ta thấy thêm hai loại nữa của khối đa diện đều. 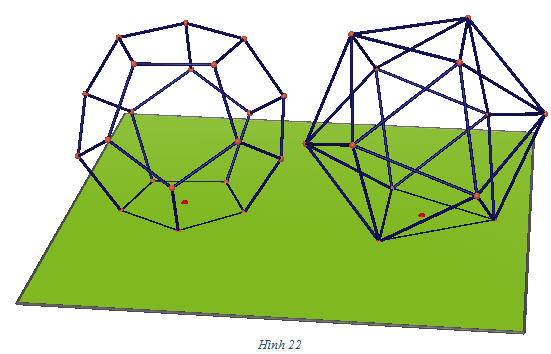
Tải trực tiếp tệp hình học động (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h22.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Người ta chứng minh được rằng chỉ có năm loại khối đa diện đều (xem bài đọc thêm Định lí Ơ-le và khối đa diện đều) và hai khối đa diện đều cùng loại thì đồng dạng với nhau. Em hãy làm thử ! Chúng ta có thể làm mô hình của năm loại khối đa diện đều bằng nguyên liệu vật liệu là bìa cứng và hồ dán. Hãy cắt bìa cứng theo mẫu dưới đây (h.23) và dán lại thành các khối đa diện đều. 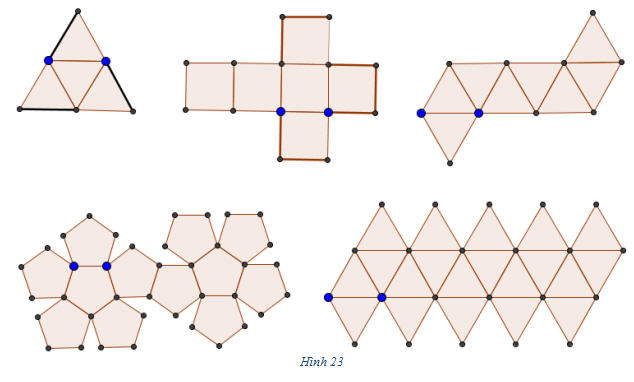
Tải trực tiếp tệp hình học động 23a (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h23a.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Tải trực tiếp tệp hình học động 23b (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h23b.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Tải trực tiếp tệp hình học động 23c (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h23c.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Tải trực tiếp tệp hình học động 23d (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h23d.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Tải trực tiếp tệp hình học động 23e (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h23e.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Câu hỏi và bài tập
11. Chứng minh rằng phép vị tự biến mỗi đường thẳng thành một đường thẳng song song hoặc trùng với nó, biến mỗi mặt phẳng thành một mặt phẳng song song hoặc trùng với mặt phẳng đó. 12. Cho một khối tứ diện đều. Hãy chứng minh rằng : a) Các trọng tâm của các mặt phẳng của nó là các đỉnh của một khối tứ diện đều ; b) Các trung điểm của các cạnh của nó là các đỉnh của một khối tám mặt đều. 13. Hai đỉnh của một khối tám mặt đều được gọi là hai đỉnh đối diện nếu chúng không cùng thuộc một cạnh của khối đó. Đoạn thẳng nối hai đỉnh đối diện gọi là đường chéo của khối tám mặt đều. Chứng minh rằng trong khối tám mặt đều : a) Ba đường chéo cắt nhau tại trung điểm của mỗi đường ; b) Ba đường chéo đôi một vuông góc với nhau ; c) Ba đường chéo bằng nhau. 14. Chứng minh rằng : a) Tâm các mặt của một khối lập phương là các đỉnh của một khối tám mặt đều ; b) Tâm các mặt của một khối tám mặt đều là các đỉnh của một khối lập phương.
Bài đọc thêm
ĐỊNH LÍ Ơ-LE VÀ KHỐI ĐA DIỆN ĐỀU 1. Đặc số Ơ-le của khối đa diện Đối với mỗi khối đa diện H, ta kí hiệu Đ là số đỉnh, C là số cạnh, M là số mặt của H và khi đó, số 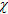 (H)=Đ-C+M được gọi là đặc số Ơ-le (còn gọi tắt là đặc số) của khối đa diện H. (Chữ Hy Lạp (H)=Đ-C+M được gọi là đặc số Ơ-le (còn gọi tắt là đặc số) của khối đa diện H. (Chữ Hy Lạp 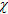 đọc là “khi”). đọc là “khi”). Các hình vẽ sau đây cho ta một khối đa diện cùng với các đặc số của chúng : 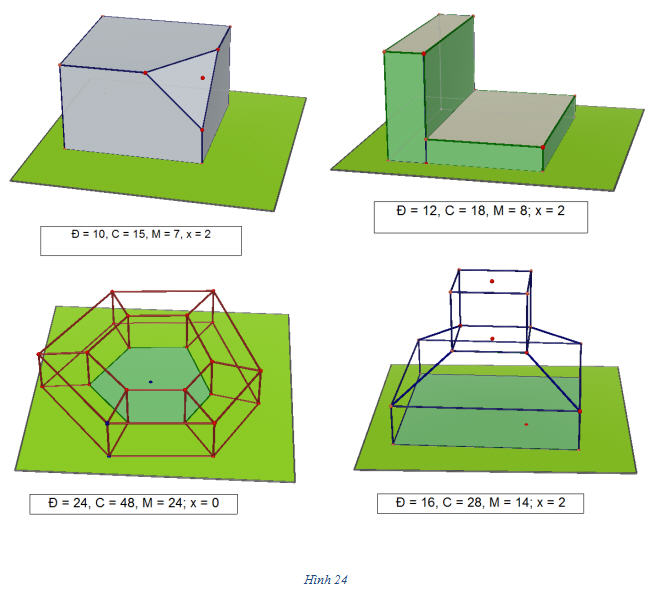
Tải trực tiếp tệp hình học động 24a (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h24a.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Tải trực tiếp tệp hình học động 24b (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h24b.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Tải trực tiếp tệp hình học động 24c (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h24c.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Tải trực tiếp tệp hình học động 24d (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch1_h24d.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Như vậy, các khối đa diện có thể có các đặc số khác nhau. Tuy nhiên, nhà toán học Thụy Sỹ Ơ-le (L.Euler) đã chứng minh định lí mang tên ông sau đây : Định lí Ơ-le. Mọi khối đa diện lồi đều có đặc số bằng 2 Ta có thể kiểm nghiệm định lí đó cho các khối đa diện đều (đó là những khối đa diện lồi). Chú ý rằng trên hình 24 có những khối đa diện không lồi nhưng vẫn có đặc số bằng 2. 2. Chứng minh định lí về năm loại khối đa diện đều Dùng định lí Ơ-le, ta có thể chứng minh rằng chỉ có năm loại khối đa diện đều. Nhắc lại : Khối đa diện đều loại {n ; p} là khối đa diện lồi có mặt là các n-giác đều và mỗi đỉnh là đỉnh chung của p cạnh. Định lí. Chỉ cho năm loại khối đa diện đều, đó là các loại : {3 ; 3}, {4 ; 3}, {3 ; 4}, {5 ; 3}, {3 ; 5}. Chứng minh. Giả sử khối đa diện đều loại {n ; p} có Đ đỉnh, C cạnh và M mặt. Vì mỗi mặt có n cạnh nên M mặt sẽ có nM cạnh, nhưng mỗi cạnh lại có chung cho hai mặt nên 2C=nM. Vì mỗi đỉnh là đỉnh chung cho p cạnh nên Đ đỉnh sẽ có pĐ cạnh, nhưng mỗi cạnh lại đi qua hai đỉnh nên 2C=pĐ. Vậy ta có pĐ = 2C = nM Từ đó suy ra 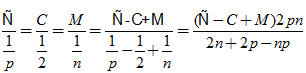
Theo định lí Ơ-le, ta có Đ – C + M = 2 nên 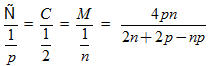
Vậy : 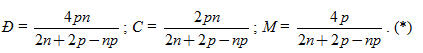
Vì các số Đ, C, M, n, p đều là những số nguyên dương nên 2n + 2p – np > 0 hay (n -2)(p - 2) < 4. Chú ý rằng n 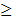 3; p 3; p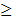 3 nên n – 2 và p – 2 là hai số nguyên dương ; ngoài ra tích số của chúng bé hơn 4. Vậy chỉ có thể sảy ra các trường hợp sau : 3 nên n – 2 và p – 2 là hai số nguyên dương ; ngoài ra tích số của chúng bé hơn 4. Vậy chỉ có thể sảy ra các trường hợp sau : 1) n – 2 = 1, p – 2 = 1 hay n = p = 3, ta có khối đa diện đều loại{3 ; 3}. Khi đó, từ (*) ta suy ra Đ = 4 , C = 6, M = 4. Đó chính là khối tứ diện đều. 2) n – 2 = 2, p – 2 = 1 hay n = 4, p = 3, ta có khối đa diện đều loại{4 ; 3}. Khi đó Đ = 8 , C = 12, M = 6. Đó chính là khối lập phương. 3) n – 2 = 1, p – 2 = 2 hay n = 3, p = 4, ta có khối đa diện đều loại{3 ; 4}. Khi đó Đ = 6 , C = 12, M = 8. Đó chính là khối tám mặt đều (còn gọi là khối bát diện đều). 4) n – 2 = 3, p – 2 = 1 hay n = 5, p = 3, ta có khối đa diện đều loại{5 ; 3}. Khi đó Đ = 20 , C = 30, M = 12. Đó chính là khối mười hai mặt đều (còn gọi là khối thập nhị diện đều). 5) n – 2 = 1, p – 2 = 3 hay n = 3, p = 5, ta có khối đa diện đều loại{3 ; 5}. Khi đó Đ = 12 , C = 30, M = 20. Đó chính là khối hai mươi mặt đều (còn gọi là khối nhị thập diện đều). Vậy ta có bảng sau đây : | Loại | Tên gọi | Số đỉnh | Số cạnh | Số mặt | | {3 ; 3} | Khối tứ diện đều | 4 | 6 | 4 | | {4 ; 3} | Khối lập phương | 8 | 12 | 6 | | {3 ; 4} | Khối tám mặt đều | 6 | 12 | 12 | | {5 ; 3} | Khối mười hai mặt đều | 20 | 30 | 8 | | {3 ; 5} | Khối hai mươi mặt đều | 12 | 30 | 20 |
Năm khối đa diện đều kể trên được nhà triết học và toán học Pla-tông (427-347 trước Công nguyên) tìm ra, chúng thường được gọi là các thể Pla-tông. Các khối đa diện theo thứ tự trong bảng trên được Pla-tông coi là tượng trưng cho lửa, đất, khí, vũ trụ và nước.
School@net
|

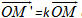 gọi là phép vị tự. Điểm O gọi là tâm vị tự, số k gọi là tỉ số vị tự.
gọi là phép vị tự. Điểm O gọi là tâm vị tự, số k gọi là tỉ số vị tự.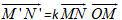 , và do đó M’N’= MN.
, và do đó M’N’= MN.
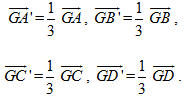

 . Khi đó dễ thấy tứ diện đều ABCD biến thành tứ diện đều A1B1C1D1 có cạnh bằng a’. Vậy tứ diện A1B1C1D1 bằng tứ diện A’B’C’D’. Theo định nghĩa, tứ diện ABCD đồng dạng với tứ diện A’B’C’D’.
. Khi đó dễ thấy tứ diện đều ABCD biến thành tứ diện đều A1B1C1D1 có cạnh bằng a’. Vậy tứ diện A1B1C1D1 bằng tứ diện A’B’C’D’. Theo định nghĩa, tứ diện ABCD đồng dạng với tứ diện A’B’C’D’. 


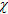 (H)=Đ-C+M được gọi là đặc số Ơ-le (còn gọi tắt là đặc số) của khối đa diện H. (Chữ Hy Lạp
(H)=Đ-C+M được gọi là đặc số Ơ-le (còn gọi tắt là đặc số) của khối đa diện H. (Chữ Hy Lạp 
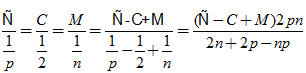
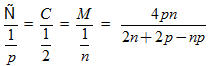
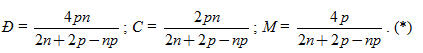
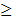 3; p
3; p




