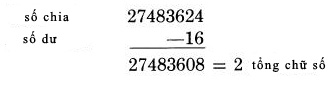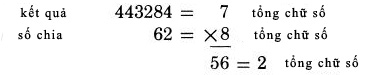Do vậy việc đầu tiên ông làm là thực hiện củng cố các kiến thức căn bản. Ông thuyết phục sinh viên rằng họ cần được dậy các vấn đề cơ sở, bằng cách mở rộng sự tự tin về kiến thức của họ. Ông bắt đầu thử thách họ bằng cách, đưa cho họ một loạt các phép nhân rất rất dài để làm việc. Trên bảng đen ông viết một số lớn, như 7,531,264 và yêu cầu họ chia nó cho một số như 9,798. Tất cả họ đều được yêu cầu tham gia và sau đó một khoảng thời gian, đủ để một sinh viên chậm chạp nhất cũng có thể hoàn thành, ông tiến hành giải đáp.

Sau đó ông xem các tờ kết quả và đối chiếu với đáp số. Tổng kết ba mươi sinh viên ông có hai nhăm kết quả khác nhau, một đúng và hai bốn kết quả sai. Sáu trong hai bốn sinh viên đã làm đúng, nhưng hai bốn sinh viên còn lại đã ít nhất mắc một lỗi trong quá trình làm bài.

Lý do làm sao ? Nhớ rằng, đó là những sinh viên đại học. Họ đều đã làm quen với các phép tính trong trường phổ thông, có những khóa học thêm về Toán ở trung học, và đã qua các đợt kiểm tra. Một thử nghiệm tương tự áp dụng trong các nhóm sinh viên khác thậm chí còn nhận được kết quả tệ hơn. Điều cần giảng giải ở đây là chúng ta đã không được dậy cách làm đúng để chắc chắn nhận được kết quả đúng. Chúng ta đã không nhận biết chính xác sự thật rằng, vấn đề chưa kết thúc chừng nào chúng ta có kết quả đúng, không chỉ dừng lại ở kết quả đã tính được. Thực tế, vấn đề vẫn chưa thực sự kết thúc cho đến khi chúng ta đã chứng minh rằng chúng ta đã có kết quả chính xác.

Trong chương cuối cùng, chúng ta sẽ nhấn mạnh vào tầm quan trọng của việc kiểm tra kết quả một cách có hệ thống. Bây giờ chúng ta làm việc với phép chia, nó thậm chí quan trọng hơn so với các cách làm ta đã làm với phép nhân và phép cộng.

Để cẩn trọng về tầm quan trọng của nó chúng ta đưa ra một lựa chọn giữa hai phương pháp chia với phép chia có số lớn. Cả hai phương pháp đều khác biệt so với phương pháp chia truyền thống.

Phương pháp đầu tiên là một phương pháp “đơn giản”, tập trung vào những người có chút ít kiến thức về toán học – đó là những người trong công việc hàng ngày chỉ yêu cầu một chút sử dụng kiến thức Toán, hoặc họ chỉ có chút ít quan tâm hạn chế về làm toán. Một phương pháp chia chính xác về phép chia số lớn cho những người như vậy phải là một phương pháp dễ nhớ và dễ áp dụng để đưa ra kết quả.

Phương pháp thứ hai là phương pháp “nhanh”. Bất cứ ai có một sở thích về các con số sẽ yêu thích nó. Nó là đủ để hỗ trợ cho những người có quan tâm đến toán học, và khi họ đã nắm được chúng, họ sẽ cảm thấy dễ dàng hơn nhiều so với phương pháp chia cũ. Đồng thời, khi đã nắm vững toàn bộ quá trình thực hiện nó, nó trở nên rất ấn tương để xem xét về chi tiết. Kết quả của phép chia có thể được viết tức thời, mà không cần phải làm các phép tính trung gian.

Phương pháp chia đơn giản:

Nó không yêu cầu một khả năng toán học nào cả. Chúng ta chỉ cần cộng lại hai số lại với nhau và sau đó thực hiện một phép trừ đơn giản.

Chúng ta thực hiện phép chia 27,483,624 cho 62. Việc thiết lập biểu diễn phép chia tương tự như cách mà mọi người thường sử dụng.

Chúng ta gọi 62 là số chia. Như cách chúng ta thực hiện, số 62 trở thành số đầu tiên của cột các chữ số. Chúng ta nhận cột này bằng cách cộng lặp liên tiếp mười lần các số 62 lại trên mỗi hàng.

Ở bên trái cột các số chia chúng ta dùng để tạo một cột các chữ số kiểm tra kết quả, sẽ có dạng: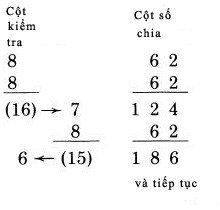

Bây giờ chúng ta nhìn vào cách chúng ta tìm các chữ số kiểm tra. Ở mỗi bước chúng ta cộng một số 62 khác vào cột số chia, do đó trong cột kiểm tra chúng ta thêm một số 8. Đó là bởi vì 8 là tổng các chữ số của 62. Khi chúng ta đi đến kết quả là số có hai chữ số (như ở trên ta có kết quả 8 cộng 8 bằng 16), chúng ta lập tức rút gọn nó thành số có một chữ số, bằng cách cộng hai chữ số của nó lại. Ví dụ ở đây ta rút gọn 16 thành 7. Sau đó chúng ta tiếp tục với ố này. Cộng thêm một số 8 tương ứng với 62 vào bước sau. Bạn có 7 cộng 8 là 15, rút gọn được thêm một lần nữa (số có hai chữ số) được 6. Cứ tiếp tục như vậy cho đến hết …

Bạn sẽ làm gì với những chữ số kiểm tra nhận được ? Bạn sẽ dùng mỗi số ngay sau khi bạn tìm được nó. Sau khi thực hiện lần cộng đầu tiên, bạn có 16 rút gọn thành 7. Để ý rằng nó nằm phía bên trái của lần cộng đầu tiên, 124. Do đó bạn kiểm tra 7 với 124. Cộng lần lượt các chữ số của số 124, bạn cũng được 7. Do đó dòng này là chính xác. Sau đó bạn cộng tiếp 62 cho 124, được 186. Ở cột kiểm tra bên trái ta bạn cộng thêm với 8 và nhận được 15, như đã nói ở trên. Rút gọn 15 ta được 6, là kết quả kiểm tra 186. Kiểm tra lại với 186, ta có 1 cộng 8 là 9, bỏ đi cả hai số và ta chỉ còn lại 6. Do 6 bằng 6, vậy hàng này được kiểm tra. Tại mỗi bước, bạn cộng thêm các số 62 vào cột số chia và cộng 8 vào cột kiểm tra. Ngay sau khi bạn hoàn thành, bạn hãy kiểm tra lại kết quả của hai cột trên.

Hiển nhiên, nếu bạn thực hiện kiểm tra tại mỗi bước như cách bạn đang thực hiện, bạn sẽ phát hiện ngay ra lỗi khi nó vừa xảy ra. Nó giúp cho việc phép chia của bạn luôn được thực hiện chính xác tại mọi thời điểm tính toán.

Nhưng bạn hãy xem số lại số lần mà bạn đã thực hiện theo cách này: 10 lần. Chính xác hơn, các số 62 được viết trên cột 10 lần, do đó bạn tiến hành cộng với nó chín lần. Kết quả sau lần cộng thứ mười sẽ là 620. Đó đơn giản là việc biến đổi số chia gốc, bằng cách thêm một số 0 vào sau nó. Ta thêm một số 0 vào cuối một số khi thực hiện nhân nó với 10. Kết quả là số thứ mười trên cột phải là số ban đầu với số 0 được ghi sau nó. Đây là toàn bộ nội dung cột với các số kiểm tra:

Kết quả 620 bằng 62 nhân 10. Đã được kiểm tra.

Khi cột các số chia được viết ra và kiểm tra chính xác bằng phương pháp tổng các chữ số, cột kiểm tra sẽ không cần dùng đến nữa và có thể được bỏ qua.

Để ý rằng chúng ta đã gán những bước đã thực hiện với các số tô đậm được ghi ở trong ngoặc. Mỗi cặp số được viết như vậy cho ta biết số 62 đã được nhân với nó. Ví dụ bên cạnh số (2) ta có kết quả 124, bằng 62 nhân với 2. Những số đánh nhãn theo kiểu này đồng thời cho ta biết các giá trị bội số của 62. Ví dụ, ta biết số 434 là một bội của 62, bởi vì 434 là 7 nhân 62. Do đó bạn sẽ thấy số 434 ở trong cột số chia, và bên cạnh nó là số chỉ vị trí (7), để xác đinh nó là kết quả của 7 nhân với 62.

Cột số chia mà chúng ta đang dùng cũng rất cần thiết để xác định trong các phép nhân, và trong các phép nhân nó là nguyên nhân chủ yếu gây lỗi. Phần còn lại của phương pháp được phát biểu thành nguyên tắc sau:

Lặp lại phép trừ từ số bị chia, với số lớn nhất mà bạn có thể thấy trong cột số chia.

Bạn bắt đầu phép trừ từ bên tay trái của số bị chia có nhiều chữ số - theo quy tắc chia thông thường. Tại mỗi bước.bạn nhìn vào cột số chia và tìm một số lớn nhất mà đủ để trừ từ số bị trừ. Hãy xem lại ví dụ: 27483624. Nếu bạn thử với hai chữ số đầu tiên bên trái, bạn có 24. Hãy nhìn vào cột số chia. Không có số nào nhỏ hơn 27. Do đó bạn lấy ba chữ số đầu của số trên, 274. Bây giờ tiếp tục nhìn vào cột số chia. Bạn hãy xem những số nào nhỏ hơn 274? (Bạn hãy xem những số nhỏ, vì phải trừ đi nó từ 274). Ở đây có bốn số 62, 124, 186, và 248. Phần còn lại đều lớn hơn 274. Do vậy số lớn nhất mà có thể thấy trong cột là 248. Từ đó, ta tiếp tục có theo quy tắc tiếp theo:

Các số được gán nhãn, hoặc các bội số của hàng được chúng ta trừ là chữ số tiếp theo của kết quả.

Ở đây số gán nhãn của 248 là (4). Do đó 4 là chữ số đầu tiên của kết quả:

Sau khi viết chữ số này vào kết quả, bạn viết lại số mà nhận được từ cột số chia bên dưới các hàng tương ứng của số bị chia, và bạn thực hiện phép trừ như biểu diễn ở trên. Bạn nhận được 26 từ kết quả phép trừ. Sau đó bạn tiếp tục dịch đến chữ số tiếp theo của số bị chia. Đó là cách bạn vẫn làm trong các phép chia thông thường.

Bây giờ bạn tiếp tục quá trình trên, sử dụng các số mới từ cột số chia ghi dưới số bị chia dài. Ở đây là 268. Bạn tiếp nhìn vào cột số chia. Ta tìm được một số lớn nhất thích hợp là 248. Trừ đi nó, và sau đó viết số gán nhãn tương ứng với nó (4) vào kết quả:

Ví dụ trên được giải quyết đầy đủ như sau:

Do đó kết quả phép chia là 443,284, và số dư là 16.

Trong thực hành, bạn sẽ có thể tìm thấy một chút thủ thuật để giảm bớt các lỗi không cần thiết. Khi ta thực hiện bảng số chia, chúng ta cần phải cộng với số chia lặp lại liên tiếp mỗi lần, nhưng chúng ta không cần thiết phải viết lại số chia nhiều lần. Bạn chỉ cần nhìn lại vào đầu cột là vị trí của số chia, để cộng các số chia với số ta nhận được kết quả gần nhất. Theo cách này, chúng ta sẽ biểu diễn lại quá trình thực hiện như sau:

Sau đây là một số ví dụ để bạn thực hành, bạn có thể tìm sự thú vị:

Có thể đôi khi xảy ra trường hợp, mặc dù điều này là không có cơ sở, rằng một người thực hiện phép chia có thể quá cẩn thận đến nỗi chọn một chữ số sai từ cột số chia. Đó là trường hợp khó có thể xảy ra bởi vì tất cả những việc ta làm theo cách này đó là tìm những số lớn ta có thể dùng được trong phép chia. Chữ số lớn nhất có thể được chấp nhận trong cột đó là số cuối cùng mà có giá trị đủ nhỏ để trừ, và mọi chữ số sau nó đều lớn hơn. Nhưng giả sử có trường hợp, ta mắc một lỗi khi nhìn vào cột. Nhưng nó vẫn không gây ra một lỗi thực sự nghiêm trọng, vì chúng ta sẽ nhận ra nó gần như tức thời ở bước đó.

(1) Nếu một ai đó chọn một số mà có giá trị quá lớn, anh ta sẽ không thể trừ đi nó.

(2) Nếu anh ta chọn một số quá nhỏ, thì ngay bước tiếp theo anh ta sẽ thấy rằng chữ số hàng kết quả sẽ là 10, đó không phải là chữ số.

Để kiểm tra phép trừ, có một cách thuận tiện và đủ mạnh để kiểm tra tất cả các phép trừ tại một thời điểm bằng cách xem lại chính kết quả. Chúng ta thực hiện bằng cách sau:

(1) Trừ đi số dư của phép chia từ số bị chia và tính tổng chữ số của số nhận được. Trong ví dụ đầu tiên ở trang 86, chúng ta còn lại số dư của 16 sau khi thực hiện phép chia.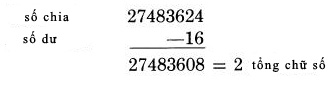

(2) Nhân tổng các chữ số của kết quả với tổng chữ số của số chia: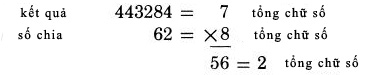

(3) So sánh hai kết quả và xem, nếu nó bằng nhau thì phép chia ta thực hiện là chính xác Trong ví dụ trên, cả hai kết quả đều là 2 do đó phép chia là chính xác.

School@net