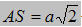Hình 87. Góc giữa hai đường thẳng.
Hai đường thẳng a, b chuyển động tự do trong không gian, mỗi đường xác định bởi hai điểm tự do. Từ điểm O chuyển động tự do trong không gian kẻ hai đường thẳng song song với a và b. Hai đường này xác định mặt phẳng P.
• Góc giữa hai đường thẳng a và b được kí hiệu là (a, b)
Theo định nghĩa ta có:
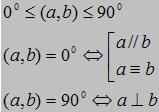
2. Góc giữa một đường thẳng và một mặt phẳng
Cho đường dthẳng a và mặt phẳng (P). Nếu a ⊥mp (P) thì như đã biết, a vuông góc với mọi đường thẳng nằm trong mp(P). Trong trường hợp đó ta nói rằng.
Hình 88. Góc giữa đường thẳng và mặt phẳng.
Đường thẳng a xác định bởi 2 điểm chuyển động tự do trong không gian.
Góc giữa đường thẳng a và mp(P) bằng 90º
Nếu a không vuông góc với mp(P) thì hình chiếu của a trên (P) là đường thẳng a', trong trường hợp đó ta có:
Định nghĩa: Góc giữa đường thẳng a và mp(P) là góc giữa đường thẳng a và hình chiếu a' củanó trên (P).
Góc giữa đường thẳng a và mp(P) đước kí hiệu là góc ( a,(P))
Theo định nghĩa trên có cũng có:
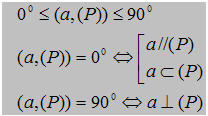
3. Góc giữa hai mặt phẳng
Cho hai mặt phẳng (P) và (Q). Gọi a và b là các đường thẳng lần lượt vuông góc với (P) và (Q). Khi đó hiển nhiên góc giữa a và b không phụ thuộc vào việc chọn hai đường thưảng a và b.
Ta gọi góc giữa a và b là góc giữa (P) và (Q) như vậy.
Hình 89. Góc giữa hai mặt phẳng.
Hai mặt phẳng P, Q xác định bởi 3 điểm chuyển động tự do trong không gian. Các đường a và b lần lượt vuông góc với P và Q.
Định nghĩa: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phảng đó.
Góc giữa hai mặt phẳng (P) và (Q) được kí hiệu là góc (P,Q)
Rõ ràng là:
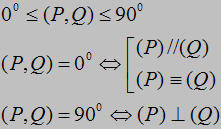
Để xác định góc giữa hai mặt phẳng (P) và (Q) cắt nhau t heo giao tuyến Δ ta có thể làm như sau:
Lấy mp(R) vuông góc với Δ , mp(R) cắt (P) và (Q) lần lượt theo các giao tuyến p và q
Hình 90. Minh họa và tính góc giữa hai mặt phẳng.
Hai mặt phẳng P, Q được xác định bởi 3 điểm chuyển động tự do trong không gian. Điểm A chuyển động trên giao tuyến d của hai mặt phẳng này. Một mặt phẳng vuông góc với giao tuyến và đi qua A (màu xanh). Từ điểm B chuyển động trên mặt phẳng màu xanh kẻ hai đường thẳng vuông góc với các mặt phẳng P, Q. Góc giữa hai đường thẳng này chính là góc giữa P và Q.
Khi đó ta có: góc (P,Q) = góc (p,q)
Thật vậy, trong (R) ta vẽ đường thẳng a ⊥ p và b⊥ q ta có a ⊥ (P) và b⊥ (Q) suy ra
Góc (P,Q) = (a,b) = (p,q)
4. Nhị diện
Ta đã biết mỗi đường thẳng a nằm trong mặt phẳng (P) chi mặt phẳng đó thành hai phần, mỗi phần cùng với đường thẳng a gọi là một nửa mặt phẳng. Đường thẳng a gọ là bờ của các nửa mặt đó
Hình 91. Khái niệm nửa mặt phẳng.
Định nghĩa: Hình hợp bởi hai nửa mặt phẳng (α) và (β), có chung bờ a gọi là nhị diện.
Mỗi nửa mặt phẳng (α) và (β) gọi là một mặt của nhị diện. Đường thẳng a gọi là cạnh của nhị diện.
Một nhị diện như thế có kí hiệu là (α, a, β) hoặc [α, β]
Hình 92. Khái niệm nhị diện.
Các nhị diện P, Q xác định bởi đường thẳng a và điểm M, N lần lượt.
Dịch chuyển các điểm M, N đẻ quan sát các nhị diện P, Q.
Nếu trên (α) ta lấy điểm M và trên (β) ta lấy điểm N (M là N đều không nằm trên a) thì nhị diện đó cũng kí hiệu là [M, a, N].
Ta hãy cắt nhị diện [α, a, β] bởi một mặt phẳng (P) vuông góc với a tại điểm O
Hình 93. Góc nhị diện.
Hình vẽ mô phỏng khái niệm góc của nhị diện. Điểm O chuyển động trên giao tuyến của hai nhị diện. Mặt phẳng P đi qua O và vuông góc với cả hai nhị diện. P giao với hai nhị diện theo hai đường thẳng x, y. Góc giữa x, y chính là góc giữa hai nhị diện.
Giao tuyến của (P) và các nửa mặt phẳng (α) và (β) lần lượt là các nửa đường thẳng Ox và Oy.
Khi đó góc xOy được ọi là góc phẳng của nhi diện (α, a, β)
Hiển nhiên là một nhị diện có nhiều góc phẳng, tuy nhiên các góc phẳng đó đều bằng nhau.
Số đo của góc phẳng nhị diện [α, β] được gọi là số đo của nhị diện [α, β] và đo của nhị diện [α, β] và được kí hiệu là:
Sđ [α, β] hay viết tắt là [α, a, β]
Ta có: 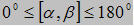
Khi 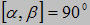 ta nói [α, a, β] là một nhị diện vuông. ta nói [α, a, β] là một nhị diện vuông.
5. Diện tích hình chiếu của một tam giác.
Định lí: Nếu một tam giác có diện tích S thì hình chiếu của nó có diện tích S' bằng tích của S với cosin của gócφ giữa mặt phẳng của tam giác và mặt chiếu.
S’=S.cosφ
Chứng minh: Gọi S là diện tích của tam giác ABC', S' là diện tích của tam giác A'B'C', hình chiếu của tam giác ABC trên mặt chiếu (P), và gọi φ là góc giữa mp(P) và mp(ABC).
Nếu φ = 900 thì công thức hiển nhiên đúng. Sau đây ta giả sử φ < 90º. Ta xét lại hai trường hợp:
Trường hợp 1: Tam giác ABC có một cạnh song song hay nằm trong mặt chiếu (P).
Giả sử cạnh AB nằm trong (P), Gọi C' là hình chiếu của đỉnh C nằm (P)
Hình 94. Định lý về diện tích hình chiếu của tam giác, trường hợp 1.
Điểm C chuyển động tự do trong không gian. A, B chuyển động tự do trên mặt phẳng P.
Trong mp(P) ta kẻ C'H ⊥ AB ta có φ=CHC’ và C’H=CH.cosφ
Do đó S’=1/2.AB.C’H’=1/2 AB.CH.cosφ
Vậy S' = Scosφ
Trường hợp 2: Tam giác ABC không có cạnh nào song song hay nằm trong mặt chiếu (P).
Ta có thể giả sử mp(P) đi qua đỉnh A sao cho các đỉnh B và C ở cùng một phía đỏi với (P).
Gọi D là giao điểm của BC với (P) và B', C' là hình chiếu của B, C trên mp(P), thế thì D thuộc D'C'
Hình 95. Định lý về diện tích hình chiếu của tam giác, trường hợp 2.
Các điểm B, C chuyển động tự do trong không gian.
Theo trường hợp 1, ta có.

Trừ từng vế hai đẳng thức (1) và (2) ta được:
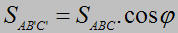
Nghĩa là ta có:
S’=S.cosφ
Bằng cách chia một đa giác thành nhiều tam giác, ta có thể mở rộng kết quả trên cho diện tích hình chiếu của một đa giác như sau:
Hệ quả: Nếu S là diện tích của một đa giác phẳng, S' là diện tích của đa giác chiếu và φ là góc giữa mặt phẳng của đa giác và mặt phẳng chiếu thì có:
S’=S.cosφ
6. Tam diện
Định nghĩa: Hình hợp bởi ba tia Ox, Oy Oz không đồng phẳng được gọi là một tam diện.
Ta kí hiệu tam diện đó là Oxyz.
Các tia Ox, Oy, Oz gọi là các cạnh của tam diện.
Các miền góc xOy, yOz, zOx gọi là các mặt của tam diện.
Độ lớn của các góc xOy, yOz, zOx gọi là các góc phẳng ở đỉnh của tam diện
Hình 96. Khái niệm tam diện.
Một tam diện gọi là tam diện vuông nếu ba góc phẳng ở đỉnh của nó đều là góc vuông
Hình 97. Tam diện vuông góc.
Muốn dịch chuyển tam diện Oxyz hãy dịch chuyển hai điểm nằm trên Ox và Oy.
7. Các ví dụ
Ví dụ 1: Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật AB = a, 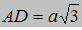 . Cạnh bên SA vuông góc với đáy và SA = . Cạnh bên SA vuông góc với đáy và SA = a. Tính:
a) Góc giữa đường thẳng SB và CD
b) Góc giữa đường thẳng SD và mp(SAB)
c) Góc giữa mặt phẳng (SCD) và (ABCD).
Giải.
a) Ta có CD //AB, từ đó:
(SB, CD)=(SB, AB)=SBA=α
Hình 98. Minh họa cho ví dụ 1.
Vì tam giác SAB vuông cân tại đỉnh A nên α = 45º.
Vậy (SB,CD)=45º
b) Ta có
AD ⊥ SA và AD ⊥ AB ⇒ AD ⊥ (SAB)
Từ đó SA là hình chiếu của SD lên mp(SAB).
Vậy: (SD, (SAB))=(SD, SA)=DSA=β
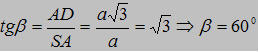
Vậy (SD,(DAB))= 60º
c) Ta có: (SCD) &tap; (ABCD) =CD
CD ⊥ AD và CD ⊥ SA ⇒ CD ⊥ (SAD)
từ đó góc giữa hai mặt phẳng (SCD) và (ABCD) chính là góc SDA=γ
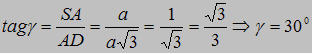
Vậy góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 30º.
Ví dụ 2: Cho lăng trụ tứ giác đều ABCD. A'B'C'D'. Một mặt phẳng α hợp với mặt đáy (ABCD) một góc 450 và cắt cạnh bên của lăng trụ tại M, N, P, Q. Tính diện tích thiết diện, biết rằng cạnh đáy của lăng trụ là a.
Giải. Gọi S là diện tích của thiết diện MNPQ. Ta có hình chiếu của MNPQ xuống mặt đáy ABCD cũng chính là hình vuông ABCD có diện tích là S’=a²
Hình 99. Minh họa cho ví dụ 2.
Thiết diện với hình hộp được xác định bởi mặt phẳng đi quan đường thẳng a và nghiêng với mặt phẳng nằm ngang một góc 45 độ.
Gọi φ là góc giữa hai mặt phẳng (MNPQ) và (ABCD); theo giả thiết ta có: φ = 45º
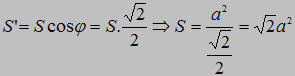
Vậy diện tích thiết diện là 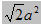
CÂU HỎI VÀ BÀI TẬP
1. Cho hình lập phương ABCD. A'B'C'D'.
a) Hãy tính góc giữa các cặp đường thẳng sau đây: AB' và BC', AC' và CD'.
b) Gọi M, N, P lần lượt à trung điểm các cạnh AB, BC, C'D'. Hãy tính góc giữa các cặp đường thẳng sau đây: MN và C'D'. BD và AD', MN và AP, A'P và DN.
2. Từ một điểm M nằm ngoài mp(P) người ta hạ đường vuông góc MA và hai đường xiên MB, MC tới mp(P). Biết MA = a, MB, MC đều tạo với mp(P) các góc 30º, và MB ⊥MC.
a) Tính đoạn BC.
b) Tính cosin góc của nhị diện [M, BC, A].
3. Cho hình chóp tam giác đều có cạnh đáy bằng 3a, cạnh bên bằng 2a.
a) Tính góc giữa cạnh bên và mặt đáy.
b) Tính tang của góc của nhị diện tạo bởi mặt bên và mặt đáy.
4. Cho lăng trụ ABC. A'B'C' có tất cả các cạnh đáy đều bằng a. Biết góc tạo thành bởi cạnh bên và mặt đáy của 600 và hình chiếu H của đỉnh.
a) Tính khoảng cách giữa hai mặt đáy.
b) Tính tang của góc giữa hai đường thẳng BC và AC'.
c) Tính tang của góc giữa mp (ABB'A') và mặt đáy.
5. Cho tam giác vuông ABC có cạnh huyền BC nằm trên mp (P). Gọi β và γ là góc hợp bởi hai đường thẳng AB, AC và mp(P). Gọi α là góc hợp bởi hai mặt phẳng (ABC) và (P).
Chứng minh rằng: sin²α = sin²β + sin² γ
6. Cho tứ diện OABC có các tam giác OAB, OBC, OCA đều là tam giác vuông tại đỉnh. O, OA = a, OB =b, OC = c. Gọi α, β, γ lần lượt là góc hợp bởi các mp(OBC), mp(OCA), mp(OAB) với mp(ABC).
Chứng minh rằng: cos²α + cos²β + cos²γ
BÀI TẬ P ÔN CHƯƠNG III
1. Hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD).
a) Chứng minh các mặt bên là những tam giác vuông.
b) Mặt phẳng (α) qua A và vuông góc với SC lần lượt cắt SB, SC, SD tại B', C', D'. Chứng minh B'D' song song với BD và AB' vuông góc với SB.
c) M là một điểm di động trên đoạn BC, gọi K là hình chiếu của S trên DM. Tìm quỹ tích các điểm K khi M di động.
d) Đặt BM = x. Tính độ dài đoạn SK theo a và x. Tính giá trị nhỏ nhất của đoạn SK.
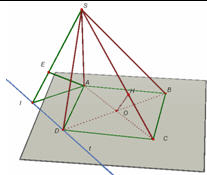
2. Hình chóp S. ABCD có đáy ABCD là hình thoi tâm O cạnh a, góc BAD=60º Đường thẳng SO vuông góc với mặt phẳng (ABCD) và đoạnSO= 3/4a . Gọi E là trung điểm của BC, F là trung điểm của BE.
a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC)
b) Tính khoảng cách từ O và A đến mặt phẳng (SBC).
c) Gọi (α)là mặt phẳng qua AD và vuông góc với mặt phẳng (SBC). Xác định thiết diện của hình chóp với (α). Tính diện tích thiết diện này.
d) Tính góc giữa (α) và mp(ABCD).
3. Cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trong hai mặt phẳng vuông góc với nhau. Gọi H, K lần lượt là trung điểm của AB, CD và E, F lần lượt là trung điểm của SA, SB.
a) Tính khoảng cách từ A đến mặt phảng (SCD) và tang của góc giưã hai mặt phẳng (SAB) và (SCD).
b) Gọi G là giao điểm của CE và DF. Chứng minh CE vuông góc với SA và DF vuông góc với SB. Tính tang của góc giữa hai mặt phẳng (GEF) và (SAB). Hai mặt phẳng này có vuông góc với nhau không?
c) Chứng minh G là trọng tâm của tam giác SHK. Tính khoảng cách từ G đến mặt phẳng (SCD).
d) Gọi M là điểm di động trên đoạn SA. Tìm quỹ tích hình chiếu của S trên mặt phẳng (CDM).
4. Trong mặt phẳng (α) cho đường tròn (O) tâm O bán kính R, CD là một đường kính cố định của (O), EF là một dây song song hoặc trùng với CD. Trên đường thẳng vuông góc với (α) tại O, ta lấy một điểm S sao cho  . Gọi H là trung điểm của EF. . Gọi H là trung điểm của EF.
a) Giả sử EF song song với CD. Chứng minh hai mặt hẳng (SEF) và (SOH) vuông góc với nhau.
b) Tính SE và SF. Chứng minh góc ESF ≤ 60º.
c) Gọi I và M lần lượt là tâm đường tròn ngoại tiếp các tam giác SCD và SEF. Giả sử 0
d) Giả sử )0 ≤OH ≤ R. Tìm tập hợp các điểm M.
5. Hình chóp S. ABCD có đáy SBCD là hình vuong cạnh a, các cạnh bên đều bằng 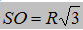
a) Tính khoảng cách từ S đến mặt phẳng (ABCD)
b) Gọi (α) là mặt phẳng qua A và vuông góc với SC. Hãy xác định thiết diện của hình chóp với (α).
c) Tính diện tích của thiết diện nói trên.
d) Gọi φ là góc giữa AB và (α). Tính Sinφ.
6. Cho hình thang ABCD có góc A và B là góc vuông, AD =2a, AB = BC = a, S là điểm nằm trên tia Ax vuông góc với mặt phẳng (ABCD). Gọi C' và D' lần lượt là hìnhc hiếu của A trên SC và SD.
a) Chứng minh góc SBC = góc SCD = 90º
b) Chứng minh AD', AC' và AB cùng nằm trong một mặt phẳng. Từ đó chứng minh rằng C'D' đi qua một điểm cố định khi S di động trên Ax.
c) Cho 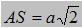 . Tính diện tích của tứ giác ABC'D'. . Tính diện tích của tứ giác ABC'D'.
d) Xác định và tính độ dài đoạn vuông góc chung của hai đường thẳng AB và SC khi 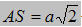
School@net
|

 1. Góc giữa hai đường thẳng.
1. Góc giữa hai đường thẳng. 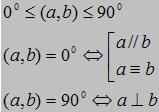
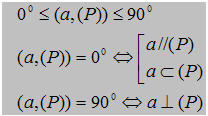
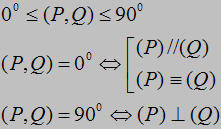
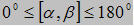
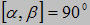 ta nói [α, a, β] là một nhị diện vuông.
ta nói [α, a, β] là một nhị diện vuông. 
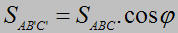
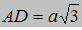 . Cạnh bên SA vuông góc với đáy và SA =
. Cạnh bên SA vuông góc với đáy và SA = 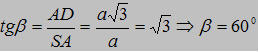
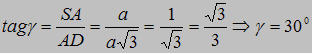
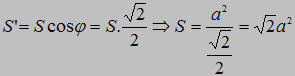
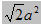
 . Gọi H là trung điểm của EF.
. Gọi H là trung điểm của EF. 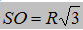
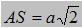 . Tính diện tích của tứ giác ABC'D'.
. Tính diện tích của tứ giác ABC'D'.