| Cong ty Cong Nghe Tin hoc Nha truong | http://www.vnschool.net |
| Ứng dụng phép nhân ma trận trong giải bài tập tin học 18/02/2010 Như tất cả chúng ta đều biết, một trong những yêu cầu không thể thiếu đối với việc giải quyết các bài tập tin học là độ phức tạp của thuật toán. Thông thường, để đạt được độ phức tạp thuật toán như mong muốn, cách làm thường là tìm ra một thuật toán ban đầu làm cơ sở, rồi từ đó dùng các kỹ năng để giảm độ phức tạp của thuật toán. Trong bài viết này, tôi xin giới thiệu với bạn đọc một phương pháp khá thông dụng: nhân ma trận. Trước khi đọc bài viết này, nếu bạn chưa có khái niệm gì về ma trận, bạn có thể tham khảo định nghĩa về ma trận trong một tài liệu khác. Trước hết, tôi xin nhắc lại tóm tắt khái niệm về phép nhân ma trận: Cho 2 ma trận: A kích thước MxN và B kích thước NxP. Kết quả phép nhân ma trận A và B là ma trận C kích thước MxP, với mỗi phần tử của ma trận C được tính theo công thức:
Để thực hiện phép nhân ma trận trên máy tính, ta có thể thực hiện thuật toán với độ phức tạp O(MNP) như sau: for i:=1 to M do for j:=1 to P do begin C[i,j]:=0; for k:=1 to N do C[i,j]:=C[i,j]+A[i,k]*B[k,j]; end; (đối với phép nhân các ma trận vuông kích thước NxN, có thuật toán nhân ma trận Strassen với độ phức tạp O(Nlog7) theo tư tưởng chia nhỏ ma trận (giống với cách nhân nhanh 2 số lớn)) tuy nhiên cài đặt rất phức tạp và nói chung không cần thiết. Thông thường, với các bài toán chúng ta gặp, phép nhân ma trận có độ phức tạp O(N3) là đủ). Cần chú ý thêm là phép nhân ma trận không có tính giao hoán (do có thể thực hiện nhân 2 ma trận A kích thước MxN và ma trận B kích thước NxP nhưng không thể thực hiện phép nhân B*A nếu P ≠ M) nhưng có tính kết hợp: (A*B)*C = A*(B*C) Ví dụ 1:Trước hết, chúng ta hãy cùng xem xét một ví dụ kinh điển nhất trong ứng dụng của phép nhân ma trận, mà thông thường ai đã học qua phần này đều biết. Dãy Fibonacci được định nghĩa như sau: F0= 1 F1= 1 ... Fi= Fi-1 + Fi-1 (i ³ 2) Yêu cầu: Cho N (N ≤ 109), tính FN Phân tích:Hiển nhiên cách làm thông thường là tính lần lượt các Fi. Tuy nhiên, cách làm này hoàn toàn không hiện quả với N lên đến 109, và ta cần một cách tiếp cận khác: Ta xét các lớp số: Lớp 1:F1, F2 Lớp 2: F2, F3 ... Lớp i: Fi, Fi+1 Ta hình dung mỗi lớp là một ma trận 1x2. Tiếp đó, ta sẽ biến đổi từ lớp i-1 đến lớp i. Sau mỗi lần biến đổi như vậy, ta tính thêm được Fi+1. Để thực hiện phép biến đổi này, chú ý là các số ở lớp sau chỉ phụ thuộc vào lớp ngay trước nó theo các phép cộng, ta tìm được cách biến đổi bằng nhân ma trận:
(Chắc hẳn đọc đến đây bạn đọc sẽ thắc mắc, làm thế nào để tìm được ma trận Để tìm được ma trận này, ta làm như sau: Ta có: Fi = 0* Fi-1 +1* Fi nên hàng đầu của ma trận là 0 1 Fi+1 = 1* Fi-1 +1* Fi nên hàng hai của ma trận là 1 1 ) Bây giờ ta sẽ cần tìm cách tăng tốc việc tính type matrix=array[0..1,0..1] of longint; const a: matrix=((0,1),(1,1)); //Định nghĩa phép nhân 2 ma trận operator * (a,b:matrix) c:matrix; var i,j,k:longint; begin fillchar(c,sizeof(c),0); for i:=0 to 1 do for j:=0 to 1 do for k:=0 to 1 do c[i,j]:=c[i,j]+a[i,k]*b[k,j]; end; //Tính a^n function power(n:longint):matrix; var temp:matrix; begin if n=1 then exit(a); temp:=cal(n div 2); temp:=temp*temp; if n mod 2=1 then temp:=temp*a; exit(temp); end; Ví dụ 2:Tiếp theo, chúng ta sẽ cùng xem xét một ví dụ tổng quát hơn của ví dụ 1. Cho số nguyên N (N ≤ 100) và 2 dãy số a1, a2, ..., aN ;b1, b2, ..., bN. Dãy số c được định nghĩa như sau:
Yêu cầu: Tính ck với k ≤ 109. (Nguồn bài: http://www.spoj.pl/problems/SEQ/ . Sau khi code các bạn có thể vào http://www.spoj.pl/register/để đăng ký thành viên và gửi bài để kiểm tra tính đúng đắn của bài làm của mình) Phân tích:Cũng như trong ví dụ 1, ta xét các lớp số: Lớp 1: c1, c2, ..., cN Lớp 2: c2, c3, ..., cN+1 ... Lớp i: ci, ci+1, ..., ci+N-1 Ta cũng sẽ áp dụng phép nhân ma trận để biến đổi từ lớp i sang lớp i+1 như sau:
(Để xây dựng ma trận vuông như trên, ta thực hiện tương tự như trong ví dụ trước: Phân tích ai+1đến ai+N dưới dạng ai đến ai+N-1 ai+1= 0*ai + 1*ai+1 + ... + 0*ai+N-1 nên hàng 1 là 0 1 0 ... 0 ... ai+N-1= 0*ai + 0*ai+1 + ... + 1*ai+N-1 nên hàng N-1 là 0 0 0 ... 1 ai+N= bN*ai + bN-1*ai+1+ ... + b1*ai+N-1 nên hàng N là bN, bN-1, ..., b1 ) Từ đó, ta thu được cách làm như trong ví dụ 1. Cài đặt cụ thể xin nhường lại cho bạn đọc. Chú ý rằng ta hoàn toàn có thể thay thế phép nhân và phép cộng trong định nghĩa phép nhân ma trận. Cụ thể hơn, thay vì Sau đây là một ví dụ minh hoạ cho nhóm các bài toán này Ví dụ 3:Cho đồ thị có hướng N đỉnh (N ≤ 100). Tính ma trận Ckkích thước NxN, với Ck[i,j] = độ dài đường đi ngắn nhất từ i đến j đi qua đúng k cạnh Phân tích: Xét ma trận A là ma trận kề của đồ thị đã cho. Hiển nhiên A = C1 C2[i,j] = min (A[i,u] + A[u,j]) với u chạy từ 1 đến N Ck[i,j] = min (Ck-1[i,u] + A[u,j]) với u chạy từ 1 đến N Như vậy, nếu ta thay phép nhân và phép cộng trong việc nhân ma trận thông thường lần lượt bởi phép cộng và phép lấy min, ta thu được một phép ”nhân ma trận” mới, tạm ký hiệu là Ä, thì
Như vậy, bài toán được đưa về bài toán tính lũy thừa của một ma trận, ta hoàn toàn có thể giải tương tự các ví dụ trước. Cài đặt phép nhân ma trận mới này hoàn toàn không phức tạp hơn cài đặt phép nhân ma trận thông thường. Việc cài đặt xin nhường lại cho bạn đọc. Ví dụ 4: Tóm tắt đề: Người ta mới tìm ra một loại vi khuẩn mới. Chúng sống thành N bầy (N ≤ 100), đánh số từ 0 đến N-1. Ban đầu, mỗi bầy này chỉ có một con vi khuẩn. Tuy nhiên, mỗi giây, số lượng vi khuẩn trong các bầy lại có sự thay đổi. Ví dụ: một bầy có thể bị chết đi, số lượng vi khuẩn trong một bầy có thể tăng lên, hoặc một bầy có thể di chuyển vị trí. Các thay đổi này tuân theo một số quy luật cho trước. Tại mỗi giây chỉ xảy ra một quy luật. Các quy luật này được thực hiện nối tiếp nhau và theo chu kỳ. Có nghĩa là, nếu đánh số các quy luật từ 0 đến M-1, tại giây thứ S thì quy luật được áp dụng sẽ là (S-1) mod M (M ≤ 1000) Nhiệm vụ của bạn là tìm xem, với một bộ các quy luật cho trước, sau T đơn vị thời gian (T ≤ 1018), mỗi bầy có bao nhiêu vi khuẩn. Các loại quy luật có thể có:
(IPSC 2003) Phân tích Cách làm đơn giản nhất là chúng ta mô phỏng lại số lượng vi khuẩn trong mỗi bầy qua từng đơn vị thời gian. Cách làm này có độ phức tạp O(T*N*(độ phức tạp xử lý số lớn)) và không thể chạy được với những test lớn. Ta hình dung số lượng vi khuẩn trong mỗi bầy trong một đơn vị thời gian là một dãy số. Như vậy, mỗi quy luật cho trước thực chất là một phép biến đổi từ một dãy số thành một dãy số mới, và ta hoàn toàn có thể thực hiện biến đổi này bằng một phép nhân ma trận. Cụ thể hơn, ta coi số lượng vi khuẩn trong N bầy tại một thời điểm xác định là một ma trận 1xN, và mỗi phép biến đổi là một ma trận NxN. Khi áp dụng mỗi phép biến đổi, ta nhân hai ma trận nói trên với nhau. Bây giờ, xét trường hợp N = 4, tôi xin lần lượt mô tả các ma trận tương ứng với các phép biến đổi:
Cũng như các bài toán trước, ta sẽ cố gắng áp dụng việc tính toán lũy thừa, kết hợp với phép nhân ma trận để giảm độ phức tạp từ T xuống logT. Tuy nhiên, có thể thấy việc sử dụng phép lũy thừa trong bài toán này phần nào phức tạp hơn bởi các ma trận được cho không giống nhau. Để giải quyết vấn đề này, ta làm như sau: Gọi Nguyễn Thành Trung |
| URL của bài viết này::http://www.vnschool.net/modules.php?name=News&file=article&sid=3782 |
| © Cong ty Cong Nghe Tin hoc Nha truong | contact: sales@schoolnet.vn |
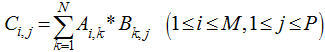
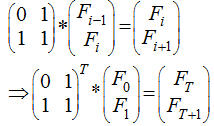
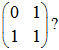
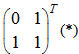 . Việc tính nhanh (*) cũng hoàn toàn tương tự việc ta tính aT với a là số nguyên. Sau đây là đoạn code minh hoạ. Trong đoạn code này, để bạn đọc dễ hiểu, tôi bỏ qua yếu tố về tính toán số lớn, và thực hiện các phép tính với kiểu số longint
. Việc tính nhanh (*) cũng hoàn toàn tương tự việc ta tính aT với a là số nguyên. Sau đây là đoạn code minh hoạ. Trong đoạn code này, để bạn đọc dễ hiểu, tôi bỏ qua yếu tố về tính toán số lớn, và thực hiện các phép tính với kiểu số longint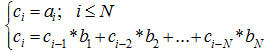
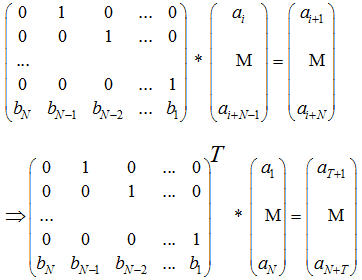
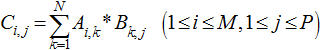 , ta có thể tính
, ta có thể tính 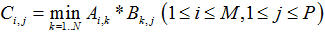 . Từ đó, ta có thể thu được một lớp các bài toán khác.
. Từ đó, ta có thể thu được một lớp các bài toán khác.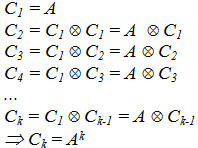


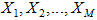 là các ma trận tương ứng với các phép biến đổi được cho. Đặt
là các ma trận tương ứng với các phép biến đổi được cho. Đặt 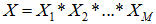 . Đặt
. Đặt 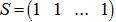
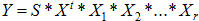 , là ma trận thể hiện số lượng vi khuẩn tại thời điểm M*t + r. Như vậy, thuật toán đến đây đã rõ. Ta phân tích T = M*t + r, nhờ đó, ta có thể giải quyết bài toán trong O(N3 * M) cho bước tính ma trận X, O(N3*(log(T/M)+M) cho bước tính Y. Bài toán được giải quyết.
, là ma trận thể hiện số lượng vi khuẩn tại thời điểm M*t + r. Như vậy, thuật toán đến đây đã rõ. Ta phân tích T = M*t + r, nhờ đó, ta có thể giải quyết bài toán trong O(N3 * M) cho bước tính ma trận X, O(N3*(log(T/M)+M) cho bước tính Y. Bài toán được giải quyết.