Với các thuật toán kể trên, mỗi khi muốn đổi chỗ 2 phần tử, chúng ta phải so sánh giá trị của 2 phần tử đó. Chính vì vậy, có thể nói là ý tưởng chính của các thuật toán này là dựa trên thao tác so sánh phần tử (Elements Comparison - EC). Quả thật cho đến nay chưa có thuật toán sắp xếp nào dựa trên ý tưởng Elements Comparison tốt hơn  . . Với một ý tưởng hoàn toàn mới, đi ngược lại với ý tưởng chính của tất cả các thuật toán trước đó, thuật toán FlashSort được phát minh bởi Karl-Dietrich Neubert là một thuật toán sắp xếp đạt đến tốc độ giới hạn về thời gian - time complexity  . Tư tưởng chính của thuật toán là dựa trên sự phân lớpphần tử (Subclasses Arrangement). FlashSort bao gồm ba khối logic:Phân loại các phần tử (Elements Classification); Phân bố các phần tử vào đúng các phân lớp (Elements Permutation); Sắp xếp các phần tử trong từng phân lớp theo đúng thứ tự (Elements Ordering). . Tư tưởng chính của thuật toán là dựa trên sự phân lớpphần tử (Subclasses Arrangement). FlashSort bao gồm ba khối logic:Phân loại các phần tử (Elements Classification); Phân bố các phần tử vào đúng các phân lớp (Elements Permutation); Sắp xếp các phần tử trong từng phân lớp theo đúng thứ tự (Elements Ordering). Elements Classification: Xuất phát từ tư tưởng: với mỗi một phần tử ai ta có thể tính toán được vị trị gần đúng ( thuộc vào một lớp ) của nó trong mảng đã sắp xếp một cách trực tiếp từ giá trị aimà không cần phải so sánh nó với các phần tử khác.Nếu giá trị phần tử lớn nhất làMax, nhỏ nhất là Min và phân các khóa thành m lớp, ta có thể tính được chỉ số lớp của phần tử aibằng công thức sau: 
Ta dùng mảng phụ L đánh dấu vị trí mphân lớp của mảng khóa a. Phân lớp thứ iđược coi là rỗng khi L[i] là vị trí chính xác phần tử cuối của phân lớp trong mảng khóa (hình 1), phân lớp i được coi là đã đầy khi mà L[i] là vị trí chính xác phần tử đầu tiên của phân lớp trong mảng khóa (hình 2). 
Khi bỏ một phần tử vào phân lớp i, ta giảm L[i] đi 1 cho đến khi về đến đúng vị trí của nó thì nghĩa là đầy (hình 2). Vậy để xác định được vị trí xuất phát cũng như vị trí kết thúc của từng phân lớp, ta phải biết được kích thước của từng phân lớp. Ban đầu, các phân lớp được coi là rỗng, L[i] được khởi gán bằng vị trí của phần tử cuối cùng của lớp i. Dễ thấy rằng, vị trí ban đầu của phân lớp thứ nhất sẽ là kích thước của nó, còn của phân lớp m sẽ là n và L[i]=L[i-1]+ kích thước của phân lớp i (hình 2). 
Elements Permutation: Giai đoạn tiếp theo là thực hiện sắp xếp các phần tử vào đúng phân lớp của nó. Việc này sẽ hình thành các chu trình hoán vị: mỗi khi ta đem một phẩn tử ở đâu đó đến một vị trí nào đó thì ta phải nhấc phần tử hiện tại đang chiếm chỗ ra, và tiếp tục với phần tử bị nhấc ra và đưa đến chỗ khác cho đến khi quay lại vị trí ban đầu thì hoàn tất vòng lặp. Với mỗi phần tử ta tính xem nó phải nằm ở phân lớp nào, rồi bỏ nó vào cái vị trí hiện tại của phân lớp đó, và vì ta bỏ vào phân lớp đó 1 phần tử nên phải lùi vị trí của phân lớp lại 1 đơn vị. Elements Ordering Trong hai giai đoạn trên ta đã chia nhỏ 1 mảng thành nhiều mảng nhỏ (phân lớp) để việc sắp xếp trở nên nhanh hơn. Công việc tiếp theo là sắp xếp thứ tự các phần tử trong mỗi phân lớp. Thuật toán Straight-Insertion Sort là lựa chọn tốt cho yêu cầu này. Dưới đây là cài đặt Flashsort thực hiện sắp xếp các khóa có kiểu số thực bằng ngôn ngữ lập trình Pascal: PROGRAM Flashsort; TYPEARR=array[1..10000]of real; VARKey:ARR; L: array[1..10000] of integer; nmin,nmax,num, cnum,i:integer; HOLD: Real; c1,c2:real; (*************************************************) PROCEDUREInput; VARi:integer;f:text; BEGIN randomize; assign(f,'d:flashsort.inp'); reset(f); Readln(f,num,cnum); for i:= 1 to num doreadln(f,Key[i]); close(f); END; (*************************************************) PROCEDURE Classification; VARi,k:integer; BEGIN nmin:=1; nmax:=1; for i:= 1 to num do begin if Key[i] < Key[nmin] then nmin:=i; if Key[i] > Key[nmax] then nmax:=i; end; c1:=round(( cnum - 1 ) / ( Key[nmax] - Key[nmin])); c2:= c1 * Key[nmin]; for k:= 1 to cnum do L[k]:=0; for i:= 1 to num do begin k:=1 + round( c1 * Key[i] - c2 ); L[k]:=L[k]+1; end; for k:= 2 to cnum do L[k]:=L[k] + L[k-1]; HOLD := Key[nmax]; Key[nmax]:=Key[1]; Key[1]:=HOLD; END; (*************************************************) PROCEDURE Permutation; VARnmove,i,j,k:integer; FLASH:real; BEGIN NMOVE:=0; j:=1; k:=cnum; while nmove < ( num - 1 ) do begin while j > L[k] do begin j:=j + 1; k:=1 + round( c1 * Key[j] - c2 ) end; FLASH:=Key[j]; while j <> ( L[k] + 1 ) do begin k:= 1 + round( c1*FLASH - c2 ); HOLD:=Key[L[k]]; Key[L[k]]:=FLASH; L[k]:=L[k]-1; FLASH:=HOLD; nmove:=nmove+1; end; end; END; (*************************************************) PROCEDURE Ordering; VARi,j:integer; BEGIN for i:= num-2 downto 1 do begin if Key[i+1] < Key[i] then begin HOLD:=Key[i]; j:=i; while Key[j+1] < HOLD do begin Key[j]:=Key[j+1]; j:=j+1; end; Key[j]:=HOLD end; end; END; (*************************************************) PROCEDURE Output; VAR i:integer; f:text; BEGIN assign(f,'flashsort.out'); rewrite(f); for i:= 1 to num do writeln(f,Key[i]:0:2,''); close(f); END; (*************************************************) BEGIN (**** main program ****) Input; Classification; Permutation; Ordering; Output; END. Nhìn lại toàn bộ các giai đoạn của thuật toán, ta thấy như sau: - Giai đoạn Classification đòi hỏi độ phức tạp O(n) và O(m), với n là số phần tử cần sắp xếp, m là số phân lớp. - Giai đoạn Permutation, mỗi phần tử chỉ phải đổi chỗ đúng một lần, do đó đòi hỏi độ phức tạp  . . - Giai đoạn Ordering mỗi 1 phân lớp đòi hỏi độ phức tạp 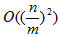 , với m phân lớp có phức tạplà , với m phân lớp có phức tạplà  . . Bằng cách điều chỉnh số lượng phân lớp có thể làm thay đổi thời gian thực hiện của thuật toán. Nếu giảm số lượng phân lớp, thời gian phân loại giảm, nhưng thời gian cho giai đoạn sắp xếp tăng (hình 3). Để tính số phân lớp tối ưu ước tính tổng thời gian thực hiện của thuật toán  . Coi m là biếncủa hàm số . Coi m là biếncủa hàm số  . Khảo sát hàm số . Khảo sát hàm số  xác định m để xác định m để  đạt giá trị cực tiểu, ta có: đạt giá trị cực tiểu, ta có:  Vậy: 
Theo một số khảo sát của các nhà phân tích thuật toán, dựa trên thực nghiệm về tốc độ chạy của chương trình,  xấp xỉ 2 và xấp xỉ 2 và  , như vậy ta có số phân lớp tối ưu là , như vậy ta có số phân lớp tối ưu là  . Nhằm mục đích khảo sát, xo sánh và khẳng định sức mạnh của thuật toán này, Karl-Dietrich Neubert đã tiến hành thực nghiệm Flashsort với Quicksort, Heapsort. Kết quả thực nghiệm thu được như hình 4. Trong trường hợp dữ liệu đầu vào cân bằng với kích thước mỗi phân lớp xấp xỉ nhau, hiệu quả về thời gian của Flashsort sẽ đạt tốt nhất. Một điều hết sức thú vị là mặc dù đạt được hiệu quả tốt về thời gian nhưng Flashsort chỉ cần đến một không gian nhớ phụ rất khiêm tốn, thông thường nó yêu cầu ít hơn 0.1n bộ nhớ phụ để sắp xếp nphần tử. . Nhằm mục đích khảo sát, xo sánh và khẳng định sức mạnh của thuật toán này, Karl-Dietrich Neubert đã tiến hành thực nghiệm Flashsort với Quicksort, Heapsort. Kết quả thực nghiệm thu được như hình 4. Trong trường hợp dữ liệu đầu vào cân bằng với kích thước mỗi phân lớp xấp xỉ nhau, hiệu quả về thời gian của Flashsort sẽ đạt tốt nhất. Một điều hết sức thú vị là mặc dù đạt được hiệu quả tốt về thời gian nhưng Flashsort chỉ cần đến một không gian nhớ phụ rất khiêm tốn, thông thường nó yêu cầu ít hơn 0.1n bộ nhớ phụ để sắp xếp nphần tử. Ngô Văn Du - ĐHSPKT NamĐịnh
School@net
|

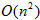 , các thuật toán phức tạp hơn là Quick Sort, Heap Sort... có độ phức tạp
, các thuật toán phức tạp hơn là Quick Sort, Heap Sort... có độ phức tạp 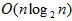 .
.  .
. . Tư tưởng chính của thuật toán là dựa trên sự phân lớpphần tử (Subclasses Arrangement). FlashSort bao gồm ba khối logic:Phân loại các phần tử (Elements Classification); Phân bố các phần tử vào đúng các phân lớp (Elements Permutation); Sắp xếp các phần tử trong từng phân lớp theo đúng thứ tự (Elements Ordering).
. Tư tưởng chính của thuật toán là dựa trên sự phân lớpphần tử (Subclasses Arrangement). FlashSort bao gồm ba khối logic:Phân loại các phần tử (Elements Classification); Phân bố các phần tử vào đúng các phân lớp (Elements Permutation); Sắp xếp các phần tử trong từng phân lớp theo đúng thứ tự (Elements Ordering).


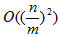 , với m phân lớp có phức tạplà
, với m phân lớp có phức tạplà  .
.  . Coi m là biếncủa hàm số
. Coi m là biếncủa hàm số  . Khảo sát hàm số
. Khảo sát hàm số  xác định m để
xác định m để 


 xấp xỉ 2 và
xấp xỉ 2 và  , như vậy ta có số phân lớp tối ưu là
, như vậy ta có số phân lớp tối ưu là  . Nhằm mục đích khảo sát, xo sánh và khẳng định sức mạnh của thuật toán này, Karl-Dietrich Neubert đã tiến hành thực nghiệm Flashsort với Quicksort, Heapsort. Kết quả thực nghiệm thu được như hình 4. Trong trường hợp dữ liệu đầu vào cân bằng với kích thước mỗi phân lớp xấp xỉ nhau, hiệu quả về thời gian của Flashsort sẽ đạt tốt nhất. Một điều hết sức thú vị là mặc dù đạt được hiệu quả tốt về thời gian nhưng Flashsort chỉ cần đến một không gian nhớ phụ rất khiêm tốn, thông thường nó yêu cầu ít hơn 0.1n bộ nhớ phụ để sắp xếp nphần tử.
. Nhằm mục đích khảo sát, xo sánh và khẳng định sức mạnh của thuật toán này, Karl-Dietrich Neubert đã tiến hành thực nghiệm Flashsort với Quicksort, Heapsort. Kết quả thực nghiệm thu được như hình 4. Trong trường hợp dữ liệu đầu vào cân bằng với kích thước mỗi phân lớp xấp xỉ nhau, hiệu quả về thời gian của Flashsort sẽ đạt tốt nhất. Một điều hết sức thú vị là mặc dù đạt được hiệu quả tốt về thời gian nhưng Flashsort chỉ cần đến một không gian nhớ phụ rất khiêm tốn, thông thường nó yêu cầu ít hơn 0.1n bộ nhớ phụ để sắp xếp nphần tử.

