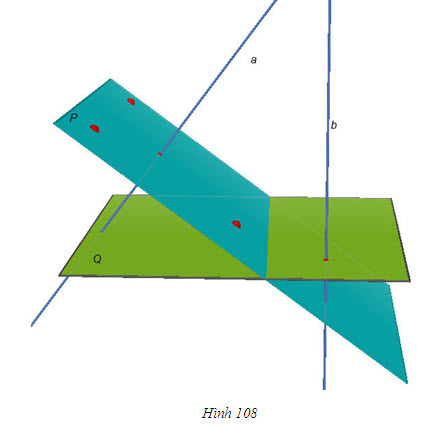
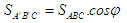 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h108.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Khi đó, góc giữa hai đường thẳng a và b không phụ thuộc vào cách lựa chọn chúng và được gọi là góc giữa hai mặt phẳng (P) và (Q). ĐỊNH NGHĨA 1  Cách xác định góc giữa hai mặt phẳng  1 1 Khi hai mặt phẳng (P) và (Q) song song hoặc trùng nhau thì góc giữa chúng bằng bao nhiêu? 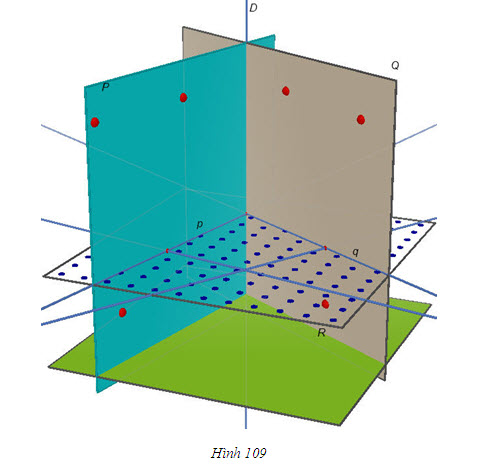 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h109.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Bây giờ, giả sử (P) và (Q) cắt nhau theo giao tuyến  . Ta vẽ một mặt phẳng (R) vuông góc với . Ta vẽ một mặt phẳng (R) vuông góc với 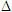 và gọi p, q lần lượt là giao tuyến của (R) với (P) và(R) với (Q). Khi đó, góc giữa (P) và (Q) bằng góc giữa p và q. và gọi p, q lần lượt là giao tuyến của (R) với (P) và(R) với (Q). Khi đó, góc giữa (P) và (Q) bằng góc giữa p và q. Thật vậy, trong mp(R), xét các đường thẳng a và b lần lượt vuông góc với p và q thì 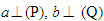 và dễ thấy góc giữa hai đường thẳng a, b bằng góc giữa hai đường thẳng p, q (h.109). Như vậy ta có: và dễ thấy góc giữa hai đường thẳng a, b bằng góc giữa hai đường thẳng p, q (h.109). Như vậy ta có: CHÚ Ý Khi hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến 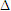 , để tính góc giữa chúng, ta chỉ , để tính góc giữa chúng, ta chỉ việc xét một mặt phẳng (R) vuông góc với  , lần lượt cắt (P) và (Q) theo các giao tuyến , lần lượt cắt (P) và (Q) theo các giao tuyến p và q. Lúc đó, góc giữa (P) và (Q) bằng góc giữa hai đường thẳng p, q. Ví dụ Cho hình chóp S.ABC có 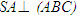 Gọi là góc giữa hai mặt phẳng (ABC) và (SBC). Chứng minh rằng Gọi là góc giữa hai mặt phẳng (ABC) và (SBC). Chứng minh rằng 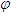 ở đây kí hiệu ở đây kí hiệu 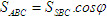 là diện tích tam giác ABC. là diện tích tam giác ABC. Giải(h.110) 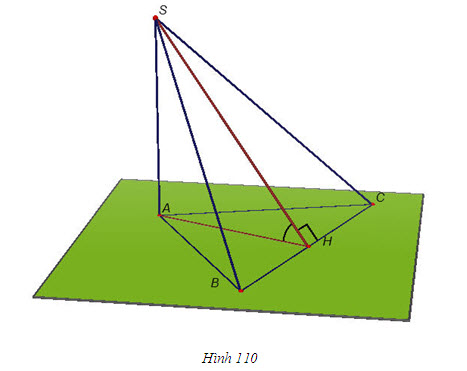 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h110.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe )
Kẻ đường cao AH của tam giác ABC. Do 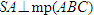 . Suy ra . Suy ra 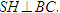 . Từ đó ta có . Từ đó ta có 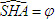 và và 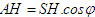 Từ đó ta có Từ đó ta có 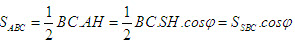 Mở rộng kết quả của ví dụ trên, ta có định lí tổng quát sau đây: ĐỊNH LÍ 1 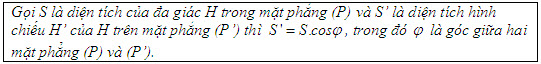 2. Hai mặt phẳng vuông góc ĐỊNH NGHĨA 2  Khi hai mặt phẳng (P) và (Q) vuông góc với nhau thì ta còn nói gọn là hai mặt phẳng (P) và (Q) vuông góc, kí hiệu 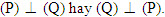  1 1 Cho hình tứ diện ABCD có AB, AC, AD đôi một vuông góc (h.111). Hãy chỉ ra các đường thẳng lần lượt vuông góc với các mặt phẳng (ABC), (ACD), (ABD) và từ đó suy ra các mặt phẳng ấy đôi một vuông góc. 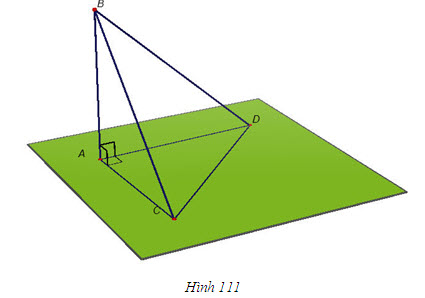 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h111.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe )
Điều kiện để hai mặt phẳng vuông góc Định lí dưới đây nói về một điều kiện để hai mặt phẳng vuông góc. ĐỊNH LÍ 2  Chứng minh(h.112) 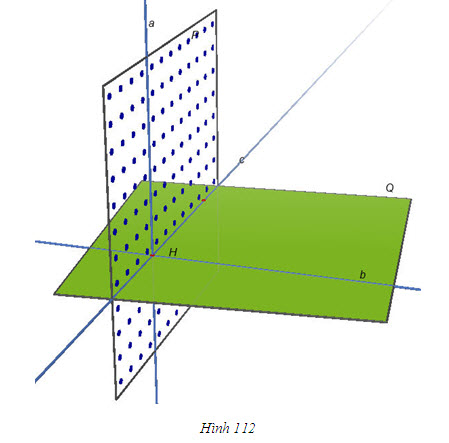 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h112.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe )
Giả sử (P) là mặt phẳng chứa đường thẳng a mà a vuông góc với mp(Q). Gọi H là giao điểm của a và (Q) thì H thuộc giao tuyến c của (P) và (Q). Trong (Q), kẻ đường thẳng b đi qua H và vuông góc với c. Khi đó, góc giữa (P) và (Q) chính là góc giữa a và b. 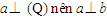 từ đó suy ra hai mặt phẳng (P) và (Q) vuông góc với nhau. từ đó suy ra hai mặt phẳng (P) và (Q) vuông góc với nhau. Ngược lại, nếu cho hai mặt phẳng vuông góc với nhau thì mặt phẳng này có chứa đường thẳng vuông góc với mặt phẳng kia hay không? Định lí 3 sau đây trả lời câu hỏi đó. Tính chất của hai mặt phẳng vuông góc ĐỊNH LÍ 3 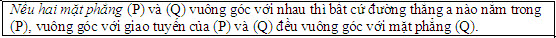 Chứng minh(h.112) Gọi c là giao tuyến của (P) và (Q),Hlà giao điểm của a và c. Trong mp(Q), kẻ đường thẳng b đi qua điểm H và vuông góc với c. Khi đó, góc giữa (P) và (Q) chính là góc giữa a và b. Vì 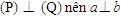 Như vậy, ta có đường thẳng a vuông góc với hai đường thẳng b , c cắt nhau cùng thuộc(Q) , suy Như vậy, ta có đường thẳng a vuông góc với hai đường thẳng b , c cắt nhau cùng thuộc(Q) , suy 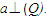 Từ định lí 2 và định lí 3, ta dễ dàng suy ra các hệ quả sau: HỆ QUẢ 1 ( h.113)  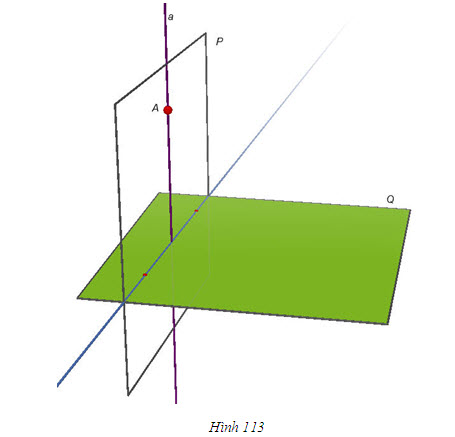 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h113.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Hệ quả 1 được viết gọn là: 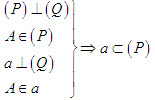 HỆ QUẢ 2(h.114) 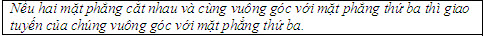 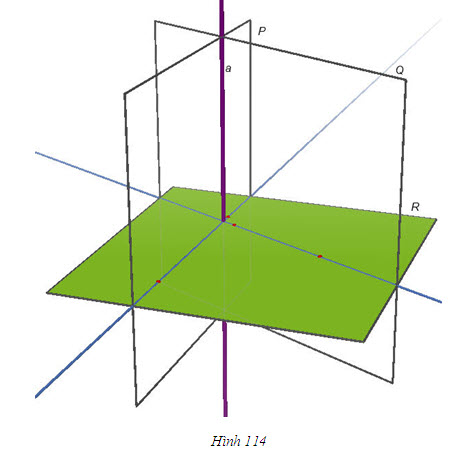 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h114.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe )
Hệ quả 2 được viết gọn là: 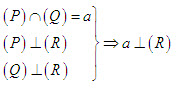 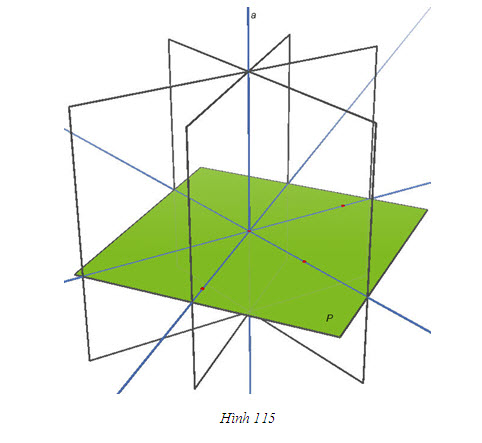 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h115.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe )
Từ định lí 2, ta nhận thấy nếu đường thẳng a vuông góc với mặt phẳng (P) thì qua a có vô số mặt phẳng vuông góc với (P) (h.115). Vậy khi a không vuông góc với (P) thì có bao nhiêu mặt phẳng chứa a và vuông góc với (P) ? Hệ quả sau sẽ trả lời câu hỏi đó. HỆ QUẢ 3   2(Để chứng minh hệ quả 3) 2(Để chứng minh hệ quả 3) Lấy điểm O thuộc a, dựng đường thẳng b đi qua điểm O và vuông góc với (P). Hãy chứng tỏ mp(a, b) chính là mp(Q) phải tìm (h.116). Sử dụng hệ quả 2 để chứng minh tính duy nhất của mặt phẳng (Q). 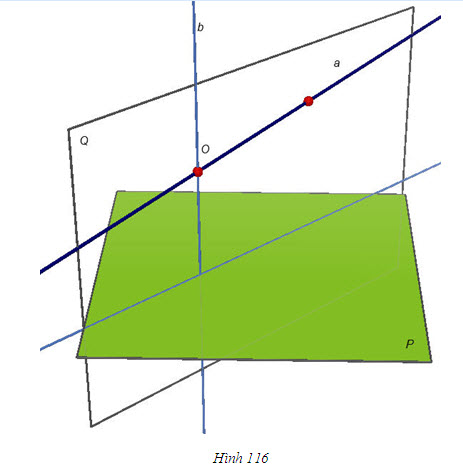 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h116.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) 3. Hình lăng trụ đứng. Hình hộp chữ nhật. Hình lập phương Trong chương II, ta đã nêu định nghĩa hình lăng trụ. Ở phần này, ta sẽ xét một số hình lăng trụ đặc biệt. Bài toán Tính độ dài đường chéo của hình hộp chữ nhật khi biết độ dài ba cạnh xuất phát từ một đỉnh là a, b, c (a, b, c gọi là ba kích thước của hình hộp chữ nhật) Giải(h.122) 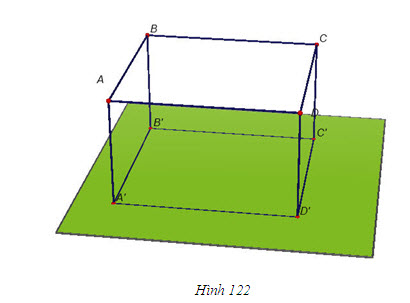 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h122.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) 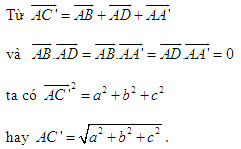 Tương tự các đường chéo còn lại cũng bằng 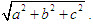  3 3 Độ dài đường chéo của hình lập phương cạnh a bằng bao nhiêu? 4. Hình chóp đều và hình chóp cụt đều ĐỊNH NGHĨA 4  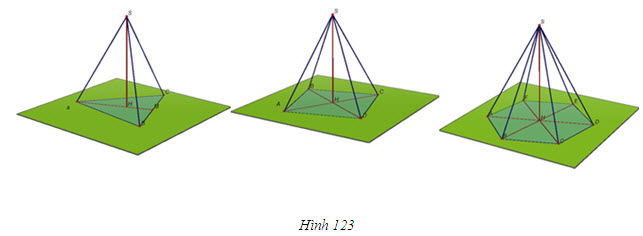 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h123a.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h123b.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h123c.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Ta biết rằng đối với một hình chóp bất kì, đường thẳng vuông góc với mặt đáy kẻ từ đỉnh gọi là đường cao của hình chóp.  4 4 Các kết quả sau đây vẽ hình chóp đều có đúng không? Vì sao? Một hình chóp là hình chóp đều khi và chỉ khi đáy của nó là đa giác đều và đường cao của hình chóp đi qua tâm của đáy (tâm của đa giác đều chính là tâm đường tròn ngoại tiếp và nội tiếp đa giác đó). Một hình chóp là hình chóp đều khi và chỉ khi đáy của nó là đa giác đều và các cạnh bên tạo với mặt đáy các góc bằng nhau. ĐỊNH NGHĨA 5 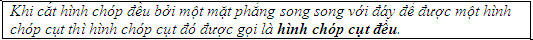 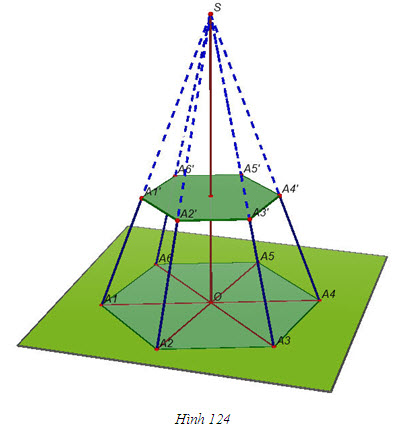 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L11_nc_ch3_h124.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe )
Đoạn nối tâm của hai đáy được gọi là đường cao của hình chóp cụt đều.  5 5 Tại sao trong hình chóp cụt đều, các mặt bên là những hình thang cân bằng nhau? Em có biết  Kim tự tháp Ai Cập Kim tự tháp Ai Cập Nhiều kim tự tháp (từ Hán - Việt nghĩa là cái tháp hình chữ kim, tức là hình chóp) đã được xây dựng ở Ai Cập bắt đầu khoảng 2500 năm trước công nguyên. Các tháp đó là những ngôi mộ của vua, hoàng hậu, … Kim tự tháp Kê-ốp (Chéops) (ở hình trên) là tháp lớn nhất. Nó được coi là một trong bảy kì quan của thế giới. Đó là một hình chóp tứ giác đều, đáy là một hình vuông có cạnh dài khoảng 230m, ngày xưa có chiều cao khoảng 147m, ngày nay chỉ còn cao 138m do bị xói mòn ở đỉnh. Trong hơn 400 năm, đó là kiến trúc cao nhất thế giới. Mãi đến thời Trung cổ mới có một số nhà thờ cao hơn. Tháp nặng khoảng 6 triệu tấn và được tạo thành bởi hơn 2 300 000 tảng đá. Ở bên trong kim tự tháp Kê-ốp có “buồng của vua” dạng hình hộp chữ nhật, dài 20 “cánh tay”, rộng 10 ”cánh tay”, cao 11,18 “cánh tay” (“cánh tay” là đơn vị độ dài thời cổ, xấp xỉ 52,5cm). Số đo khá lẻ 11,18 này đã hấp dẫn các nhà khảo cứu: phải chăng có thể giải thích điều này khi tính độ dài đường chéo hình hộp và độ dài đường chéo mặt bên của hình hộp đó? Câu hỏi và bài tập 21. Các mệnh đề sau đúng hay sai? a) Hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì song song với nhau; b) Hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì vuông góc với nhau; c) Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước; d) Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì luôn đi qua một đường thẳng cố định; f) Hình lăng trụ có hai mặt bên là hình chữ nhật là hình lăng trụ đứng; g) Hình chóp có đáy là đa giác đều và ba cạnh bên bằng nhau là hình chóp đều. 22. Cho hình hộp ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Nếu 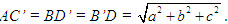 thì hình hộp đó có phải là hình hộp chữ nhật không? Vì sao? 23. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. a) Chứng minh rằng AC’ vuông góc với hai mặt phẳng (A’BD)và (B’CD’). b) Cắt hình lập phương bởi mặt phẳng trung trực của AC’. Chứng minh thiết diện tạo thành là một lục giác đều. Tính diện tích thiết diện đó. 24. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và 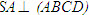 , SA = x. Xác định x để hai mặt phẳng (SBC) và (SDC) tạo với nhau góc . , SA = x. Xác định x để hai mặt phẳng (SBC) và (SDC) tạo với nhau góc . 25. Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến 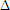 . LấyA , B cùng thuộc . LấyA , B cùng thuộc 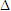 và lấy và lấy 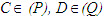 sao cho sao cho 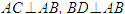 và AB = AC = BD. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng và AB = AC = BD. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng 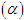 đi qua điểm A và vuông góc với CD. Tính diện tích thiết diện khi AC = AB = BD = a. đi qua điểm A và vuông góc với CD. Tính diện tích thiết diện khi AC = AB = BD = a. 26. Hình hộp ABCD.A’B’C’D’ là hình hộp gì nếu thỏa mãn một trong các điều kiện sau? a) Tứ diện AB’CD’ có các cạnh đối bằng nhau; b) Tứ diện AB’CD’ có các cạnh đối vuông góc; c) Tứ diện AB’CD’ là tứ diện đều. 27. Cho hai tam giác ACD, BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Gọi I, J lần lượt là trung điểm của AB và CD. a) Tính AB, IJ theo a và x. b) Với giá trị nào của xthì hai mặt phẳng (ABC) và (ABD) vuông góc? 28. Cho tam giác ABC và mặt phẳng (P). Biết góc giữa mp(P) và mp(ABC) là 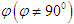 ; hình chiếu của tam giác ABC trên mp(P) là tam giác A’B’C’. Chứng minh rằng ; hình chiếu của tam giác ABC trên mp(P) là tam giác A’B’C’. Chứng minh rằng 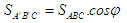 Hướng dẫn. Xét hai trường hợp: a) Tam giác ABC có một cạnh song song hoặc nằm trong mp(P); b) Tam giác ABC không có cạnh nào song song hay nằm trong mp(P).
School@net
|



 1
1
 . Ta vẽ một mặt phẳng (R) vuông góc với
. Ta vẽ một mặt phẳng (R) vuông góc với 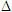 và gọi p, q lần lượt là giao tuyến của (R) với (P) và(R) với (Q). Khi đó, góc giữa (P) và (Q) bằng góc giữa p và q.
và gọi p, q lần lượt là giao tuyến của (R) với (P) và(R) với (Q). Khi đó, góc giữa (P) và (Q) bằng góc giữa p và q. và dễ thấy góc giữa hai đường thẳng a, b bằng góc giữa hai đường thẳng p, q (h.109). Như vậy ta có:
và dễ thấy góc giữa hai đường thẳng a, b bằng góc giữa hai đường thẳng p, q (h.109). Như vậy ta có: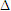 , để tính góc giữa chúng, ta chỉ
, để tính góc giữa chúng, ta chỉ  , lần lượt cắt (P) và (Q) theo các giao tuyến
, lần lượt cắt (P) và (Q) theo các giao tuyến 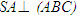 Gọi là góc giữa hai mặt phẳng (ABC) và (SBC). Chứng minh rằng
Gọi là góc giữa hai mặt phẳng (ABC) và (SBC). Chứng minh rằng 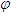 ở đây kí hiệu
ở đây kí hiệu 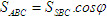 là diện tích tam giác ABC.
là diện tích tam giác ABC.
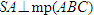 . Suy ra
. Suy ra 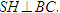 . Từ đó ta có
. Từ đó ta có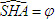 và
và 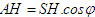 Từ đó ta có
Từ đó ta có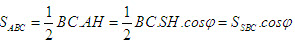
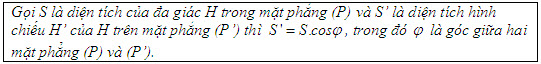

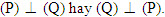
 1
1
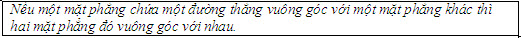

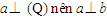 từ đó suy ra hai mặt phẳng (P) và (Q) vuông góc với nhau.
từ đó suy ra hai mặt phẳng (P) và (Q) vuông góc với nhau.
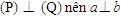 Như vậy, ta có đường thẳng a vuông góc với hai đường thẳng b , c cắt nhau cùng thuộc(Q) , suy
Như vậy, ta có đường thẳng a vuông góc với hai đường thẳng b , c cắt nhau cùng thuộc(Q) , suy 


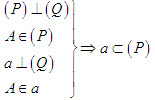
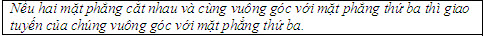

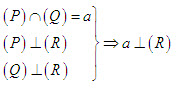


 2(Để chứng minh hệ quả 3)
2(Để chứng minh hệ quả 3)

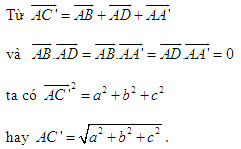
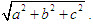
 3
3

 4
4

 Kim tự tháp Ai Cập
Kim tự tháp Ai Cập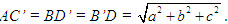
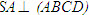 , SA = x. Xác định x để hai mặt phẳng (SBC) và (SDC) tạo với nhau góc .
, SA = x. Xác định x để hai mặt phẳng (SBC) và (SDC) tạo với nhau góc .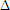 . LấyA , B cùng thuộc
. LấyA , B cùng thuộc 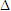 và lấy
và lấy 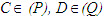 sao cho
sao cho 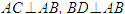 và AB = AC = BD. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng
và AB = AC = BD. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng 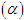 đi qua điểm A và vuông góc với CD. Tính diện tích thiết diện khi AC = AB = BD = a.
đi qua điểm A và vuông góc với CD. Tính diện tích thiết diện khi AC = AB = BD = a.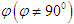 ; hình chiếu của tam giác ABC trên mp(P) là tam giác A’B’C’. Chứng minh rằng
; hình chiếu của tam giác ABC trên mp(P) là tam giác A’B’C’. Chứng minh rằng