Bài toán 1: Cho đường tròn (O;R) và hình vuông có cạnh a (a > 2R). Trên (O;R) lấy điểm M bất kì, trên hình vuông lấy điểm N bất kì, Gọi I là trung điểm của MN. Tìm quỹ tích của điểm I khi M, N lần lượt di động trên các đường tròn và hình vuông trên. Khi khảo sát bài toán này trên phần mềm Cabri ta làm theo trình tự sau:
+ Vẽ đường tròn (O;R) và hình vuông cạnh a.
+ Lấy M, N lần lượt thuộc đường tròn và hình vuông, chọn đoạn MN rồi vào Midpoint (chức năng phần mềm CabriII plus) để xác định trung điểm I.
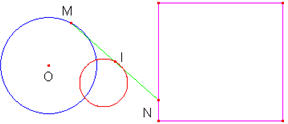
+ Vào Locus rồi chọn I và chọn M ta đợc quỹ tích của điểm I theo M (lúc đó coi như N cố định) là đường tròn (O’; R/2) như sau:
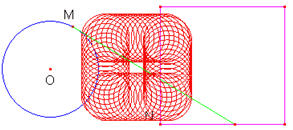
 + Vào Trace on/off rồi chọn (O’) và vào Animation sau đó chọn N ta được dấu vết quỹ tích của (O’) như hình dưới đây:
+ Vào Trace on/off rồi chọn (O’) và vào Animation sau đó chọn N ta được dấu vết quỹ tích của (O’) như hình dưới đây:
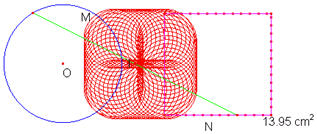
 Hình có màu nền đỏ chính là quỹ tích điểm I. Như vậy quỹ tích điểm I là một hình vuông bít tròn bốn góc và có lỗ thủng hình vuông ở trung tâm. Vậy miền quỹ tích đó được xác định cụ thể bằng suy luận như thế nào ?
Hình có màu nền đỏ chính là quỹ tích điểm I. Như vậy quỹ tích điểm I là một hình vuông bít tròn bốn góc và có lỗ thủng hình vuông ở trung tâm. Vậy miền quỹ tích đó được xác định cụ thể bằng suy luận như thế nào ?
Phần thuận:
Trước hết ta thấy nếu cố định N và M chuyển động trên (O;R) thì quỹ tích trung điểm I là đường tròn (O’;R/2) với O’ là trung điểm của ON.
Dễ thấy quỹ tích của O’ khi N chuyển động là hình vuông cạnh a/2 có tâm K’ (là trung điểm của OK). Ta xét hình thù của phần mặt phẳng mà (O’;R/2) quét lên khi O’ chuyển động trên hình vuông A’B’C’D’:
Khi O’ chạy trên cạnh A’B’, B’C’, C’D’, D’A’ thì đường tròn (O’) lần lượt quét lên mặt phẳng các lục giác cong A1B1UF1E1E, B1UJC1XY, JC1D1VH1G1, D1VTA1ZW. Vì điều kiện a >2R nên các lục giác cong này không lấp đầy hình vuông mà còn để khuyết một khoảng là hình vuông có cạnh bằng (a/2)-R nằm ở trung tâm hình vuông A’B’C’D’.
Phần đảo:
Lấy điểm I’ bất kì thuộc thuộc một trong 6 lục giác nêu trên, giả sử I’ thuộc lục giác A1B1UF1E1T (các trường hợp khác chứng minh tương tự).
Dựng đường tròn (I’; R/2), vì I’ thuộc lục giác nên (I’) cắt TU tại ít nhất một điểm, gọi một trong các giao điểm đó là O’. Vì A’là trung điểm của OA và A’O’//AM’ (M’ là giao điểm của OO’ và AB) suy ra O’ là trung điểm của OM’. Dựng bán kính ON’ của đường tròn (O’) song song với O’I’, lại có O’I’ = ON’/2 suy ra I’ là trung điểm của M’N’.
Vậy quỹ tích điểm I là hình vuông có kích thước (a/2)+R có bít tròn bốn góc bởi các 1/4 đường tròn bán kính R/2, ở trung tâm bị rỗng bởi một hình vuông kích thước bằng (a/2)-R.
* Nhận xét: Bài toán trên ta xét quỹ tích điểm I trong trường hợp (a/2)>R. Vậy trong các trường hợp khác thì sao?
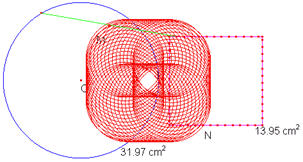
+ Nếu (a/2)< R ta có hình như miền quỹ tích điểm I như sau:
 + Nếu R >(a/2) ta có hình như miền quỹ tích điểm I như sau:
+ Nếu R >(a/2) ta có hình như miền quỹ tích điểm I như sau:
 Việc chứng minh bài toán trong các trường hợp này xin dành cho bạn đọc.
Việc chứng minh bài toán trong các trường hợp này xin dành cho bạn đọc.
Đặng Văn Biểu-THCS Đô
|







