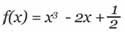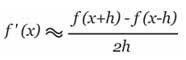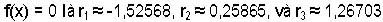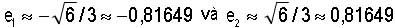Trước hết ta hiển thị các trục toạ độ bằng công cụ [Thuộc tính]Hiện các Trục. Sau đó ta tạo biểu thức tương ứng trong vùng làm viêc. Một biểu thức đặt trong vùng làm việc có thể được tính với các giá trị khác nhau của biến. Ở đây ta kích hoạt công cụ [Văn bản và Biểu tượng]Biểu thức và vào biểu thức x^3 - 2*x + 1/2. Các tên có thể gán cho các biến là các chữ a,b,c,...,z. Đặt điểm P trên trục hoành (bằng công cụ [Điểm] Điểm). Sau đó ta có được toạ độ điểm P bằng công cụ [Đo]Toạ độ hoặc Phương trình sau khi chọn điểm P. Văn bản sẽ hiển thị toạ độ mà ban đầu sẽ gắn cho P, và sẽ thay đổi tương ứng với sự dịch chuyển của điểm này. Với công cụ [Thao tác]Chọn, ta có thể tách rời các toạ độ của điểm P và đặt tại một vị trí bất kì trên vùng làm việc. Ta cũng có thể gắn các toạ độ này lại với điểm P bằng cách dịch chuyển nó gần vào điểm P.

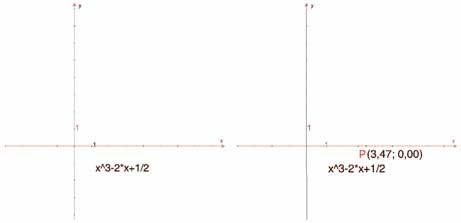
Hình2.1 - [Bên Trái]. Ta nhập vào biểu thức tương ứng với hàm số cần nghiên cứu. [Bên Phải]. Ta đặt điểm P trên trục hoành và ta hiển thị các toạ độ bằng công cụ [Đo]Toạ độ hoặc Phương trình.

Bây giờ ta tính giá trị f(x) trong đó x là hoành độ điểm P. Để thực hiện điều đó, ta kích hoạt công cụ và ta chọn hoành độ của P từ văn bản biểu thị các toạ độ của P.

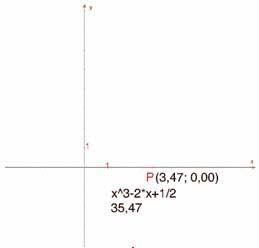
Hình 2.2 – Công cụ [Đo] Áp dụng một Biểu thức được dùng để tính giá trị của f(x) với x là hoành độ của điểm P

Sau đó ta chuyển giá trị này lên trục tung bằng công cụ [Dựng hình]Chuyển độ Đo, bằng cách chọn giá trị cần chuyển, sau đó trọn trục tung. Sau đó ta chỉ cần dựng các đường thẳng song song với các trục và đi qua hai điểm này ([Dựng hình] Đường thẳng Song song) và ta thu được giao điểm M có toạ độ (x, f(x)). Trên hình 2.3, ta đã chuyển P so với vị trí của nó ở hình 2.2 để dẫn đến điểm thuộc trục tục thu được bằng cách chuyển độ đo và điểm đó thuộc phần hiển thị được của vùng làm việc.

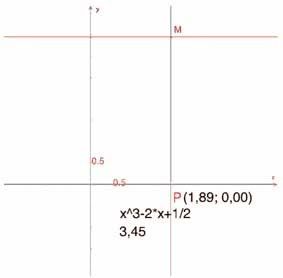
Hình 2.3 - Dựng điểm M(x, f(x)).

Ta thu được đồ thị của hàm số bằng cách hiển thị tập hợp điểm M khi P chạy trên trục hoành. Ta dựng tập hợp điểm này với công [Dựng hình]Tập hợp điểm và chọn điểm M, rồi sau đó là điểm P. Để có thể hiển thị một cách tốt nhất phần của đồ thị mà ta quan tâm nghiên cứu, ta có thể dịch chuyển gốc của hệ trục toạ độ và các khoảng chia trên trục bằng cách rê-trượt gốc của toạ độ hoặc điểm chia đơn vị bất kì.

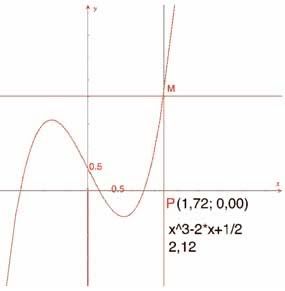
Hình 2.4 – Công cụ [Dựng hình]Tập hợp điểm cho phép dựng đồ thị của hàm số.

Ta sẽ dựng một cách gần đúng một tiếp tuyến với cong tại một điểm. Đối với giá trị h nhỏ, ta có :

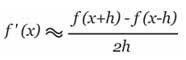
Theo quan điểm hình học, công thức tính gần đúng này tương đương với việc lấy phương của tiếp với đường cong tại điểm có hoành độ x là phương của đường thẳng nối các điểm có hoành độ x- h và x+ h. Với công cụ [Văn bản và Biểu tượng]Số, ta nhập một giá trị cho h, chẳng hạn ở đây là 0,3 cho phép dựng. Sau đó ta có thể nhập một số khác nhỏ hơn để có một sự xấp xỉ tốt hơn. Sau đó ta dựng điểm A trên trục hoành và dựng đường tròn tâm A và bán kính h nhờ công cụ [Dựng hình] Đường tròn bằng cách chọn h và sau đó là A. Hai giao điểm của đường tròn này với trục hoành có hoành độ tương ứng là x- h và x+ h, ở đó x là hoành độ của điểm A. Tiếp theo ta dựng ba đường thẳng song với trục tung và đi qua hai giao điểm trên, điểm A nhờ công cụ [Dựng hình] Đường thẳng song song.

Ta gọi các giao điểm của các đường song song này với đường cong lần lượt là B-, B, B+ và chúng sẽ có hoành độ tương ứng là x- h, x, và x + h.

Vì hình vẽ đã phức tạp hơn nhiều, bây giờ ta sẽ che các yếu tố mà ta không dùng đến nữa. Ta kích hoạt công cụ [Thuộc tính]Che/Hiện và ta chọn các yếu tố cần che. Ở đây ta sẽ che các điểm P, M, hai đường thẳng để dựng điểm M, các toạ độ của P và ảnh của hoành độ của P qua hàm số. Các đối tượng bị che không được hiển thị nữa, và khi mà công cụ [Thuộc tính]Che/Hiện được kích hoạt thì các đường biểu diễn chúng sẽ biến thành đứt đoạn. Để hiển thị lại một lần nữa công cụ này, ta chỉ cần chọn chúng lại một lần nữa bằng công cụ nói trên.

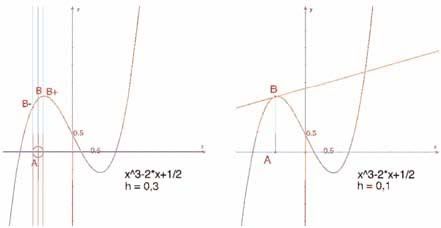
Hình 2.5 - [Bên Trái]. Bằng cách lấy giao điểm của điểm tròn tâm A bán kính h, ta dựng ba điểm của đồ thị có hoành độ lần lượt là x-h, x, và x+h.
[Bên phải]. Việc dựng gần đúng tiếp tuyến tại B thu được bằng cách dựng đường thẳng song song với đường thẳng (B- B+) và đi qua B.

Ta dựng đường thẳng này nhờ công cụ [Đường]Đường thẳng và sau đó đường thẳng song song với [Dựng hình] Đường thẳng Song song. Sau đó ta che đường thẳng (B- B+) và các yếu tố khác của phép dựng và chỉ để lại các yếu tố h, A,B và tiếp tuyến tại B được hiển thị.

Ta thấy rằng giá trị h = 0,3 cho ta một sự xấp xỉ tiếp tuyến khá tốt. Tuy nhiên ta còn có thể nâng cao chất lượng sự xấp xỉ này bằng cách thu nhỏ giá trị h, ví dụ lấy h bằng 0,0001.

Việc dịch chuyển điểm A trên trục cho phép xác định bằng trực giác ba nghiệm của phương trình f(x) = 0, hai cực trị địa phương của f và điểm uốn của đồ thị.

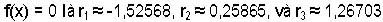
Hoành độ các điểm cực trị là

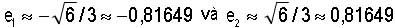
Điểm uốn có toạ độ (0 ; 1/2).

Bài tập 10* - Sử dụng hệ số góc của tiếp tuyến để dựng đồ thị của hàm số đạo hàm

Bài tập 11* - Tiếp tuyến này cắt trục hoành tại điểm A’. Nói chung điểm này là một nghiệm xấp xỉ tốt hơn giá trị x nếu như điểm A đã ở lân cận của một nghiệm của phương trình f(x) = 0. Nhận xét này chính là cơ sở của phương pháp lặp Newton1 - Raphson2 để tìm nghiệm gần đúng của phương trình. Dựng điểm A’, sau đó ta lặp lại cách dựng để có điểm A’’, sau đó khảo sát vị trí của điểm A’’ so với vị trí của điểm A. Đặc biệt ta có thể tìm được hai vị trí của điểm A khác với ba nghiệm sao cho điểm A’’ quay trở lại điểm A.

Để có thêm thông tin đó là hai nghiệm gần đúng của một đa thức bậc 6 là - 0,56293 và 0,73727. Ta cũng có thể thấy rằng việc chọn không tốt điểm A sẽ dẫn đến các điểm tương ứng không hội tụ về nghiệm và sẽ dẫn A’ đến một trong hai điểm mà ở đó đạo hàm bằng không.

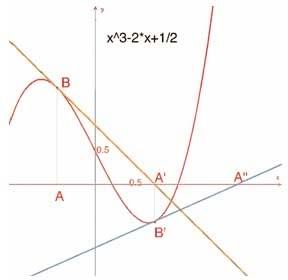
Hình 2.6 – Hai bước lặp đầu tiên theo phương pháp Newton-Raphson bắt đầu từ điểm A.

Chú ý : Ta có thể thu được đồ thị của hàm số này bằng cách sử dụng công cụ [Đo]Áp dụng một biểu thức. Đầu tiên chọn biểu thức rồi sau đó chọn một trong hai trục.

School@net