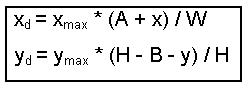Dễ thấy, khi muốn mô phỏng một vật thể hay một hình phẳng (mà ta gọi chung là đối tượng), trong đó nếu cần thể hiện các thông số về kích thước, ta luôn phải gắn đối tượng đó vào một hệ tọa độ. Hệ tọa độ này (mà ta gọi là hệ tọa độ ngoài) do chúng ta tự chọn gốc, phương chiều các trục, đơn vị trên trục sao cho phù hợp với những điều kiện cụ thể thuận lợi cho việc giải quyết vấn đề. Tuy nhiên khi biểu diễn cùng đối tượng đó lên màn hình máy tính, chúng ta cần có phép chuyển hệ tọa độ nhằm đảm bảo đúng mọi tính chất đặc trưng về hình học của đối tượng. Vấn đề không đơn giản như phép đổi hệ tọa độ chúng ta đã được học, bới hệ tọa độ màn hình có gốc tọa độ là điểm trên cùng bên trái màn hình, trục x nằm ngang hướng sang phải, trục y vuông góc với trục x, có chiều đi xuống. Hệ tọa độ màn hình chỉ sử dụng đơn vị là pixel và tọa độ các điểm biên của đối tượng không được vượt quá độ phân giải hiện thời của màn hình đồ họa. Trong khi đó, hệ tọa độ ngoài, các trục có độ dài tùy ý(hay vô tận), và hệ tọa độ màn hình cũng không tồn tại các tọa độ âm. Tất nhiên màn hình máy tính có thể mô phỏng các đối tượng có kích thước rất lớn, nhưng một điều chắc chắn là các kích thước đó phải hữu hạn. Thông thường để dễ dàng hơn trong việc biểu diễn đối tượng lên màn hình, chúng ta nên biểu diễn nó trong hệ tọa độ ngoài, tiếp đó nhờ vào công thức chuyển hệ trục tọa độ để có thể tìm ra tọa độ của đối tượng đó trong hệ tọa độ màn hình. Vậy mấu chốt của vấn đề ở chỗ tìm ra công thức chuyển đổi đó. Như đã nói, vì kích thước đối tượng là hữu hạn nên ta có thể thiết rằng đối tượng có thể được biểu diễn trong một hệ tọa độ ngoài (nằm trên một tờ giấy chẳng hạn) bị giới hạn trong một hình chữ nhật có kích thước lần lượt là W và H (hay cũng chính là kích thước của tờ giấy). Trên tờ giấy đó có hệ tọa độ ngoài xOy với gốc tọa độ O cách mép trái tờ giấy khoảng cách A và cách mép dưới tờ giấy khoảng cách B. Biểu diễn đối tượng lên màn hình cũng chính là biểu diễn tất cả các điểm trên đối tượng đó lên màn hình, nên không mất tính tổng quát ta có thể coi đối tượng cần biểu diễn như một điểm Q có tọa độ (x,y) nằm trong hệ tọa độ xOy. Giả sử điểm Q này khi qua phép chuyển trục tọa độ trở thành điểm Q' có tọa độ (xd,yd) nằm trong hệ tọa độ màn hình. Ta cần tìm được giá trị xd, yd qua các giá trị đã biết. 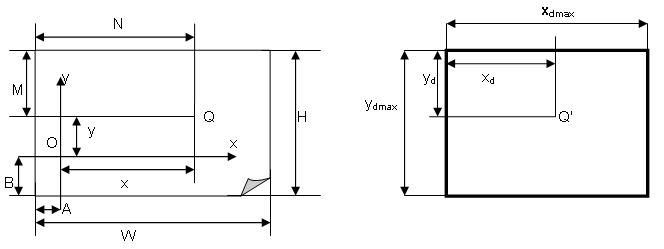
Gọi M là khoảng cách giữa Q tới mép trên của tờ giấy, N là khoảng cách giữa Q tới mép trái tờ giấy, dựa vào hình vẽ ta có: M = H - (B + y) và N = A + x. Ta có tỷ số chiều rộng và cao của điểm Q trong hệ tọa độ ngoài là: N / W = (A + x) / W(1) M / H = (H - B - y) / H(2) Trong hệ tọa độ màn hình, tỷ số chiều rộng và cao của điểm Q' được tính bởi tỷ số giữa xd với độ phân giải ngang và giữa yd với độ phân giải đứng của màn hình. Giá trị độ phân giải màn hình đồ họa như ta đã biết, là do người lập trình quy định (khi khởi tạo chế độ đồ họa) và có thể được thay đổi theo một số cặp giá trị phù hợp mà màn hình đó được hỗ trợ. Chúng ta có thể gọi độ phân giải màn hình đang sử dụng là xmax và ymax. Khi đó trong hệ tọa độ màn hình, điểm Q' có tỷ số chiều rộng là xd /xmax(3) và tỷ số chiều cao là yd / ymax (4). Để đảm bảo đúng tính chất hình học của đối tượng, tỷ số chiều rộng và cao trong hệ tọa độ màn hình của Q' và trong hệ tọa độ ngoài của Q phải tương ứng bằng nhau. Điều đó có nghĩa là: (1) = (3) và (2) = (4). Tức là ta có: (A + x) / W = xd / xmax và (H - B - y) / H = yd / ymax Do đó ta dễ dàng rút ra được công thức tính xd, yd là: 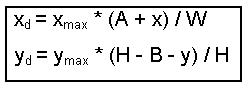 Nhận xét rằng: vì M luôn không âm, nên (H - B - y) cũng không âm. Mặt khác do đối tượng luôn nằm trong tờ giấy nên nếu x < 0 thì |x| <= A nên chắc chắn rằng dù điểm Q có tọa độ (x,y) mang giá trị âm thì tọa độ Q' tương ứng trên màn hình máy tính không bao giờ có kết quả âm. Nếu sau phép chuyển đổi thu được tọa độ không nguyên thì chúng ta cần đưa giá trị đó về số nguyên gần nhất. Cần lưu ý sử dụng đơn vị khoảng cách phù hợp cho các giá trị đã biết và phải có sự thống nhất để đảm bảo giá trị trả về có số pixel đủ lớn để khi thể hiện lên màn hình có thể quan sát đối tượng bằng mắt thường. Ví dụ, nếu đối tượng được thể hiện trong hệ tọa độ ngoài nằm trên giấy A4, nếu chúng ta dùng đơn vị của trục là cm sẽ có thể cho ta một giá trị tọa độ quá nhỏ so với việc sử dụng đơn vị trục là mm.
Nguyễn Tuấn Nghĩa
Schoolnet
|