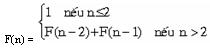Trong Toán học, ta cũng thường hay gặp các định nghĩa đệ qui:
1) Số tự nhiên:
a) 1 là một số tự nhiên
b) x là số tự nhiên nếu x-1 là số tự nhiên
2) Hàm giai thừa: n!
a) 0!=1
b) Nếu n>0 thì n! = n(n -1)!
* Giải thuật đệ qui và thủ tục đệ qui
Nếu lời giải của một bài toán T được thực hiện bằng lời giải của một bài toán T có dạng giống như T, thì đó là một lời giải đệ qui. Giải thuật tương ứng với lời giải như vậy gọi là giải thuật đệ qui.
Thoạt nghe thì các bạn thấy có vẻ hơi lạ nhưng điểm mấu chốt cần lưu ý là: T? tuy có dạng giống như T, nhưng theo một nghĩa nào đó, nó phải "nhỏ" hơn T.
Hãy xét bài toán tìm một từ trong một quyển từ điển. Có thể nêu giải thuật như sau:
if Từ điển là một trang
then Tìm từ trong trang này
else begin
Mở từ điển vào trang giữa
Xác định xem nửa nào của từ điển chứa từ cần tìm
if Từ đó nằm ở nửa trước của từ điển
then Tìm từ đó trong nửa trước
else Tìm từ đó trong nửa sau
end;
Tất nhiên giải thuật trên mới chỉ được nêu dưới dạng "thô" và còn nhiều chỗ chưa cụ thể, chẳng hạn:
- Tìm từ trong một trang thì làm thế nào
- Thế nào là mở từ điển vào trang giữa
- Làm thế nào để biết từ đó nằm ở nửa nào của từ điển...
Để trả lời rõ những câu hỏi trên không phải là khó, nhưng ta sẽ không sa vào các chi tiết này mà muốn tập trung vào việc xét "chiến thuật" lời giải. Có thể hình dung chiến thuật tìm kiếm này một cách khái quát như sau:
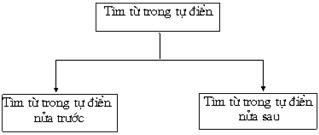
Ta thấy có hai điểm chính cần lưu ý:
1. Sau mỗi lần từ điển được tách đôi thì một nửa thích hợp sẽ lại được tìm kiếm bằng một "chiến thuật? như đã dùng trước đó.
2. Có một trường hợp đặc biệt, khác với mọi trường hợp trước, sẽ đạt được sau nhiều lần tách đôi, đó là trường hợp tự điển chỉ còn duy nhất một trang. Lúc đó việc tách đôi ngừng lại và bài toán trở thành đủ nhỏ để ta có thể giải quyết trực tiếp bằng cách tìm từ mong muốn trên trang đó chẳng hạn, bằng cách tìm tuần tự. Trường hợp đặc biệt này được gọi là trường hợp suy biến.
Có thể coi đây là một "chiến thuật " kiểu "chia để trị". Bài toán được tách thành bài toán nhỏ hơn và bài toán nhỏ hơn lại được giải quyết với thuật chia để trị như trước, cho tới khi xuất hiện trường hợp suy biến.
Ta thể hiện giải thuật tìm kiếm này dưới dạng một thủ tục:
Procedure TIMKIEM (TD,Tu)
{TD được coi là đầu mối để truy nhập được vào tự điển đang xét, Tu chỉ từ cần tìm}
1. if Tự điển chỉ còn là một trang
then Tìm từ Tu trong trang này
else begin
2. Mở tự điển vào trang giữa
Xác định xem nửa nào của tự điển chứa từ Tu
if Tu nằm ở nửa trước của tự điển
then call TIMKIEM (TD 1,Tu)
else call TIMKIEM (TD 2,Tu)
end;
{TD 1 và TD 2 là đầu mối để truy nhập được vào nửa trước và nửa sau của từ điển}
3. Return
Thủ tục như trên được gọi là thủ tục đệ qui. Từ đó, có thể nêu ra mấy đặc điểm sau:
a) Trong thủ tục đệ qui có lời gọi đến chính thủ tục đó. ở đây, trong thủ tục TIMKIEM có call TIMKIEM.
b) Mỗi lần có lời gọi lại thủ tục thì kích thước của bài toán đã thu nhỏ hơn trước. ở đây khi có call TIMKIEM thì kích thước từ điển chỉ còn bằng một "nửa" trước đó.
c) Có một trường hợp đặc biệt: trường hợp suy biến. Đó chính là trường hợp mà từ điển chỉ còn là một trang. Khi trường hợp này xảy ra thì bài toán còn lại sẽ được giải quyết theo một cách khác hẳn và gọi đệ qui cũng kết thúc. Chính tình trạng kích thước của bài toán cứ giảm dần sẽ đảm bảo dẫn tới trường hợp suy biến.
Một số ngôn ngữ lập trình như Pascal chẳng hạn, cho phép viết các thủ tục đệ qui. Nếu thủ tục chứa lời gọi đến chính nó, như thủ tục TIMKIEM ở trên thì nó được gọi là đệ qui trực tiếp. Cũng có dạng thủ tục chứa lời gọi đến thủ tục khác mà ở thủ tục này lại chứa lời gọi đến nó. Trường hợp này gọi là đệ qui gián tiếp.
* Thiết kế giải thuật đệ qui
Khi bài toán đang xét hoặc dữ liệu đang xử lý được định nghĩa dưới dạng đệ qui thì việc thiết kế các giải thuật đệ qui tỏ ra rất thuận lợi. Hầu như nó phản ánh rất sát nội dung của định nghĩa đó. Các bạn có thể thấy điều này qua bài toán sau:
* Bài toán Dãy số FIBONACCI
Dãy số Fibonacci bắt nguồn từ bài toán cổ về việc sinh sản của các cặp thỏ. Bài toán được đặt ra như sau:
1) Các con thỏ không bao giờ chết.
2) Hai tháng sau khi ra đời một cặp thỏ mới sẽ sinh ra một cặp thỏ con (một đực và một cái).
3) Khi đã sinh con rồi thì cứ mỗi tháng tiếp theo chúng lại sinh được một cặp con mới.
Giả sử bắt đầu từ một cặp mới ra đời thì đến tháng thứ n sẽ có bao nhiêu cặp?
Ví dụ: n=6, ta thấy:
Tháng thứ 1: 1 cặp (cặp ban đầu)
Tháng thứ 2: 1 cặp (cặp ban đầu vẫn chưa đẻ)
Tháng thứ 3: 2 cặp (đã có thêm 1 cặp con)
Tháng thứ 4: 3 cặp (cặp đầu vẫn đẻ thêm)
Tháng thứ 5: 5 cặp (cặp con bắt đầu đẻ)
Tháng thứ 6: 8 cặp (cặp con vẫn đẻ tiếp)
Bây giờ ta xét tới việc tính số cặp thỏ ở tháng thứ n: F(n)
- Nếu mỗi cặp thỏ ở tháng thứ (n-1) đều sinh con thì F(n) = 2(n-1).
Nhưng không phải như vậy. Trong các cặp thỏ ở tháng thứ (n-1) chỉ có những cặp đã có ở tháng thứ (n-2) mới sinh con ở tháng thứ n được thôi.
Do đó: F(n) = F(n-2) + F(n-1)
Vì vậy có thể tính F(n) theo
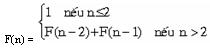
Dãy số thể hiện F(n) ứng với các giá trị của n= 1, 2, 3,... có dạng:
1 1 2 3 5 8 13 21 34 55...
được gọi là dãy số Fibonacci.
Dãy số Fibonacci còn là mô hình của rất nhiều hiện tượng tự nhiên và cũng được sử dụng nhiều trong tin học. Sau đây là thủ tục đệ qui thể hiện giải thuật tính F(n):
Function F(n)
1. if n <= 2 then F:=1
else F:=F(n-2) + F(n-1)
2. Return
ở đây chỉ có một chi tiết hơi khác là trường hợp suy biến ứng với hai giá trị F(1) = 1 và F(2)=1.
Qua ví dụ trên, ta có thể thấy: Đệ qui là một công cụ để giải các bài toán. Đối với bài toán trên, việc thiết kế các giải thuật đệ qui tương ứng khá thuận lợi vì thuộc dạng tính giá trị hàm mà định nghĩa đệ qui của hàm đó xác định được dễ dàng. Nhưng không phải lúc nào tính đệ qui trong cách giải bài toán cũng thể hiện rõ nét và đơn giản như vậy.
Có những bài toán, bên cạnh giải thuật đệ qui vẫn có những giải thuật lặp khá đơn giản và hữu hiệu. Chẳng hạn, giải thuật lặp tính số Fibonacci có thể viết:
Function FIBONACCI(n)
1. if n<=2 then FIBONACCI:=1;
2. Fib1:=1; Fib2:=2;
3. For i:=3 to no do begin
Fibn:=Fib1 + Fib2;
Fib1:=Fib2;
Fib2:=Fibn
end;
4. FIBONACCI:=Fibn;
return
Khi thay các giải thuật đệ qui bằng các giải thuật không tự gọi chúng, như giải thuật lặp nêu trên, được gọi là khử đệ qui.
Tuy vậy, đệ qui vẫn có vai trò xứng đáng của nó. Có những bài toán, việc nghĩ ra lời giải đệ qui thuận lợi hơn nhiều so với lời giải lặp và có những giải thuật đệ qui thực sự cũng có hiệu lực cao nữa. Mặt khác, về mặt định nghĩa, công cụ đệ qui đã cho phép xác định một tập vô hạn các đối tượng bằng một phát biểu hữu hạn. Các bạn có thể làm quen với cách giải bài toán đệ qui qua các bài tập sau:
* Bài tập
1. Hãy viết một thủ tục đệ qui in ra tất cả các hoán vị của n phần tử của một dãy số a={a1, a2,.., an}. Ví dụ n=3, a1 = 1, a2 = 2, a3 =3, thì in ra: 123; 132; 213; 231; 312; 321.
2. Viết một thủ tục đệ qui thực hiện in ngược một dòng ký tự cho trước. Ví dụ cho dòng PASCAL thì in ra LACSAP.
Quang Hưng( đăng trên THNT
|

 * Khái niệm về đệ qui
* Khái niệm về đệ qui