1. Định nghĩa tích của một vectơ với một số
Xét các vectơ trên hình 20. Ta hãy chú ý đến hai vectơ  và và 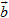 . Hai vectơ đó có cùng hướng, và độ dài vectơ . Hai vectơ đó có cùng hướng, và độ dài vectơ 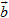 bằng hai lần độ dài vectơ bằng hai lần độ dài vectơ  , tức là , tức là 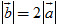 . Trong trường hợp đó ta viết . Trong trường hợp đó ta viết 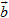 = 2 = 2 và nói rằng: Vectơ và nói rằng: Vectơ 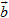 bằng 2 nhân với vectơ bằng 2 nhân với vectơ  (hoặc bằng vectơ (hoặc bằng vectơ  nhân với 2), hoặc vectơ nhân với 2), hoặc vectơ 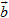 là tích của vectơ là tích của vectơ  với số 2. với số 2.
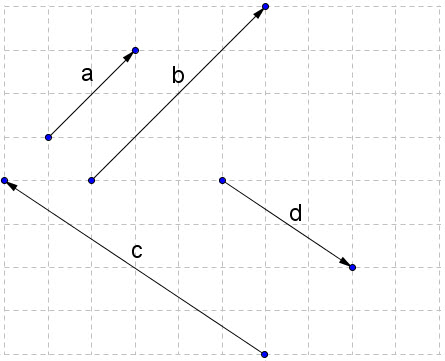
Hình 20
Tải trực tiếp tệp hình học động: L10_nc_ch1_h20.ggb Xem trực tiếp hình vẽ động trên màn hình.
Lại chú ý đến hai vectơ 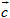 và và 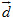 . Hai vectơ này ngược hướng, và . Hai vectơ này ngược hướng, và 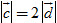 . Khi đó ta viết . Khi đó ta viết 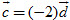 và nói rằng: Vectơ và nói rằng: Vectơ 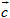 bằng -2 nhân với vectơ bằng -2 nhân với vectơ 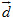 (hoặc bằng vectơ (hoặc bằng vectơ 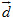 nhân với -2), hoặc vectơ nhân với -2), hoặc vectơ 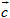 là tích của vectơ là tích của vectơ 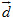 với -2. với -2.
 1. Vẽ hình bình hành ABCD. 1. Vẽ hình bình hành ABCD.
a) Xác định điểm E sao cho 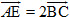 . .
b) Xác định điểm F sao cho 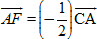 . .
ĐỊNH NGHĨA
Tích của vectơ  với số thực k là một vectơ, kí hiệu là k với số thực k là một vectơ, kí hiệu là k , được xác định như sau , được xác định như sau
1) Nếu k 0 thì vectơ k cùng hướng với vectơ cùng hướng với vectơ  ; ;
Nếu k < 0 thì vectơ k ngược hướng với vectơ ngược hướng với vectơ  ; ;
2) Độ dài vectơ k bằng bằng 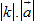 . .
Phép lấy tích của một vectơ với một số gọi là phép nhân vectơ với số (hoặc phép nhân số với vectơ).
Nhận xét. Từ định nghĩa ta thấy ngay 1 = =  , (˗1) , (˗1)  là vectơ đối của là vectơ đối của  , tức là (˗1) , tức là (˗1)  = ˗ = ˗ . .
Ví dụ. Trên hình 21, ta có tam giác ABC với M và N lần lượt là trung điểm hai cạnh AB và AC. Khi đó ta có
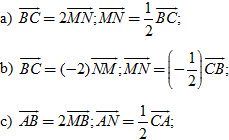
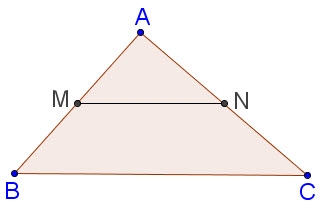
Hình 21
Tải trực tiếp tệp hình học động: L10_nc_ch1_h21.ggb Xem trực tiếp hình vẽ động trên màn hình.
2. Các tính chất của phép nhân vectơ với số
Dựa vào định nghĩa phép nhân vectơ với số ta có thể chứng minh các tính chất sau đây

 2. (Để kiểm chứng tính chất 3 với k = 3) 2. (Để kiểm chứng tính chất 3 với k = 3)
a) Vẽ tam giác ABC với giả thiết 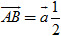 và và 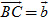 . .
b) Xác định điểm A' sao cho 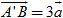 và điểm C' sao cho và điểm C' sao cho 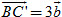 . .
c) Có nhận xét gì về hai vectơ 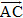 và và 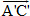 ? ?
d) Hãy kết thúc việc chứng minh tính chất 3 bằng cách dùng quy tắc ba điểm.
CHÚ Ý
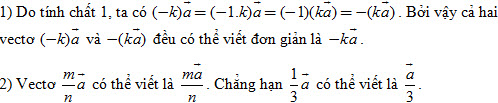
Bài toán 1. Chứng minh rằng điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi với điểm M bất kì, ta có 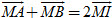 . .
Giải. (h. 22) Với điểm M bất kì, ta có
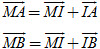
Như vậy
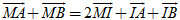
Ta biết rằng I là trung điểm của AB khi và chỉ khi 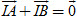 . Từ đó suy ra điều phải chứng minh. . Từ đó suy ra điều phải chứng minh.
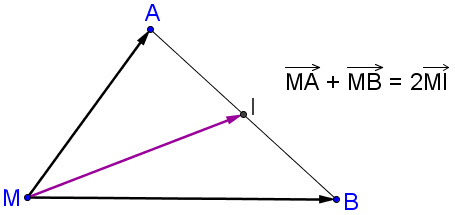
Hình 22
Tải trực tiếp tệp hình học động: L10_nc_ch1_h22.ggb Xem trực tiếp hình vẽ động trên màn hình.
Bài toán 2. Cho tam giác ABC với trọng tâm G. Chứng minh rằng với điểm M bất kì, ta có
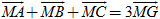
 3. (Để giải bài toán 2) (h. 23) 3. (Để giải bài toán 2) (h. 23)
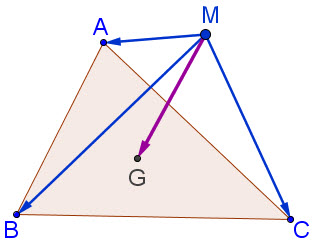
Hình 23
Tải trực tiếp tệp hình học động: L10_nc_ch1_h23.ggb Xem trực tiếp hình vẽ động trên màn hình.
a) Tương tự Bài toán 1, hãy biểu thị các vectơ 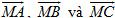 qua vectơ qua vectơ 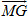 và từng vectơ và từng vectơ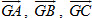 . .
b) Tính tổng 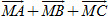 . Với chú ý rằng G là trọng tâm tam giác ABC, hãy suy ra điều phải chứng minh. . Với chú ý rằng G là trọng tâm tam giác ABC, hãy suy ra điều phải chứng minh.
3. Điều kiện để hai vectơ cùng phương
Ta đã biết rằng nếu 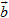 = k = k thì hai vectơ thì hai vectơ  và và 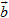 cùng phương. Điều ngược lại có đúng hay không? cùng phương. Điều ngược lại có đúng hay không? 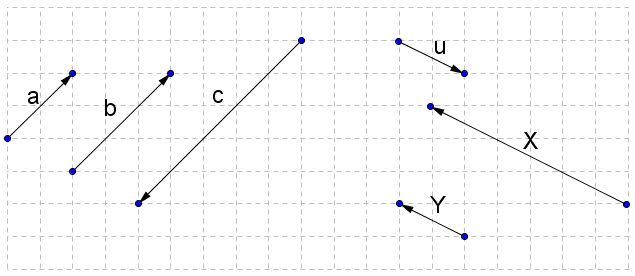
Hình 24
Tải trực tiếp tệp hình học động: L10_nc_ch1_h24.ggb Xem trực tiếp hình vẽ động trên màn hình.
?1. Xem hình 24. Hãy tìm các số k, m, n, p, q sao cho  . .
Một cách tổng quát ta có

?2. Trong phát biểu ở trên, tại sao phải có điều kiện  ? ?
Điều kiện để ba điểm thẳng hàng

Chứng minh. Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vectơ 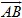 và và 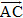 cùng phương. Bởi vậy theo trên ta phải có cùng phương. Bởi vậy theo trên ta phải có 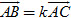 . .
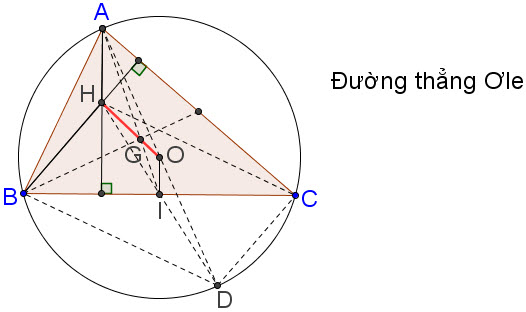
Bài toán 3. Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O.
a) Gọi I là trung điểm của BC. Chứng minh 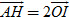 . .
b) Chứng minh 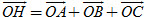 . .
c) Chứng minh ba điểm O, G, H thẳng hàng.
Giải. (h. 25)
Hình 25
Tải trực tiếp tệp hình học động: L10_nc_ch1_h25.ggb Xem trực tiếp hình vẽ động trên màn hình.
a) Dễ thấy 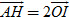 nếu tam giác ABC vuông. nếu tam giác ABC vuông.
Nếu tam giác ABC không vuông, gọi D là điểm đối xứng của A qua O. Khi đó
BH // DC (vì cùng vuông góc với AC),
BD // CH (vì cùng vuông góc với AB).
Suy ra BDCH là hình bình hành, do đó I là trung điểm của HD. Từ đó
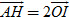 . .
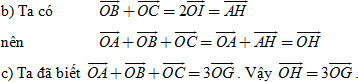
Suy ra ba điểm O, G, H thẳng hàng.
Đường thẳng đi qua ba điểm này gọi là đường thẳng Ơle của tam giác ABC.
4. Biểu thị một vectơ qua hai vectơ không cùng phương
Cho hai vectơ  và và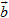 . Nếu vectơ . Nếu vectơ 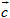 có thể viết dưới dạng có thể viết dưới dạng 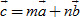 , với m và n là hai số thực nào đó, thì ta nói rằng: Vectơ , với m và n là hai số thực nào đó, thì ta nói rằng: Vectơ 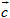 biểu thị được qua hai vectơ biểu thị được qua hai vectơ  và và 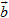 . .
Một câu hỏi đặt ra là: Nếu đã cho hai vectơ không cùng phương  và và 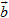 thì phải chăng mọi vectơ đều có thể biểu thị được qua hai vectơ đó? thì phải chăng mọi vectơ đều có thể biểu thị được qua hai vectơ đó?
Ta có định lí sau đây
ĐỊNH LÍ

Chứng minh
Từ một điểm O nào đó, ta vẽ các vectơ 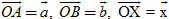 (h. 26). (h. 26).
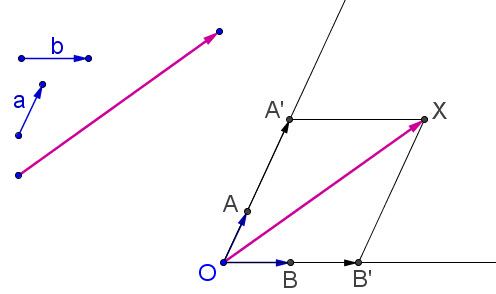
Hình 26
Tải trực tiếp tệp hình học động: L10_nc_ch1_h26.ggb Xem trực tiếp hình vẽ động trên màn hình.
Nếu điểm X nằm trên đường thẳng OA thì ta có số m sao cho 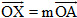 . .
Vậy ta có 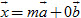 (lúc này n = 0). (lúc này n = 0).
Tương tự, nếu điểm X nằm trên đường thẳng OB thì ta có
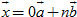 (lúc này m = 0). (lúc này m = 0).
Nếu điểm X không nằm trên OA và OB thì ta có thể lấy điểm A' trên OA và B' trên OB sao cho OA'XB' là hình bình hành. Khi đó ta có 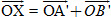 , và do đó có các số m, n sao cho , và do đó có các số m, n sao cho 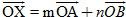 , hay , hay
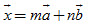
Bây giờ nếu còn có hai số m' và n' sao cho 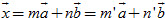 , thì , thì 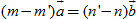 . .
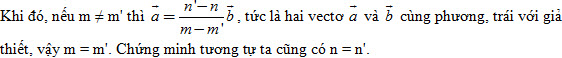
Câu hỏi và bài tập
21. Cho tam giác vuông cân OAB với OA = OB = a. Hãy dựng các vectơ sau đây và tính độ dài của chúng
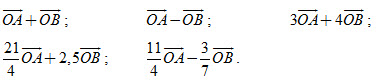
22. Cho tam giác OAB. Gọi M, N lần lượt là trung điểm hai cạnh OA và OB. Hãy tìm các số m và n thích hợp trong mỗi đẳng thức sau đây
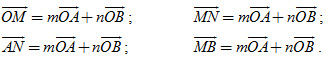
23. Gọi M và N lần lượt là trung điểm các đoạn thẳng AB và CD. Chứng minh rằng
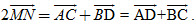
24. Cho tam giác ABC và điểm G. Chứng minh rằng
a) Nếu 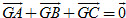 thì G là trong tâm tam giác ABC; thì G là trong tâm tam giác ABC;
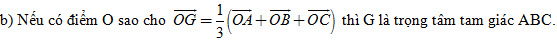
25. Gọi G là trọng tâm tam giác ABC. Đặt 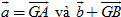 . Hãy biểu thị mỗi vectơ . Hãy biểu thị mỗi vectơ 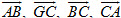 qua các vectơ qua các vectơ  và và 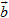 . .
26. Chứng minh rằng nếu G và G' lần lượt là trọng tâm tam giác ABC và tam giác A'B'C' thì
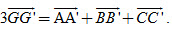
27. Cho lục giác ABCDEF. Gọi P, Q, R, S, T, U lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác PRT và QSU có trọng tâm trùng nhau.
28. Cho tứ giác ABCD. Chứng minh rằng
a) Có một điểm G duy nhất sao cho 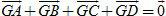 . Điểm như thế gọi là trọng tâm của bốn điểm A, B, C, D. Tuy nhiên, người ta vẫn quen gọi G là trọng tâm của tứ giác ABCD. . Điểm như thế gọi là trọng tâm của bốn điểm A, B, C, D. Tuy nhiên, người ta vẫn quen gọi G là trọng tâm của tứ giác ABCD.
b) Trọng tâm G là trung điểm của mỗi đoạn thẳng nối các trung điểm hai cạnh đối của tứ giác, nó cũng là trung điểm của đoạn thẳng nối trung điểm hai đường chéo của tứ giác.
c) Trọng tâm G nằm trên các đoạn thẳng nối một đỉnh của tứ giác và trọng tâm của tam giác tạo bởi ba đỉnh còn lại.
School@net
|

 cộng với chính nó thì ta có thể nói kết quả là hai lần vectơ
cộng với chính nó thì ta có thể nói kết quả là hai lần vectơ 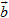 . Hai vectơ đó có cùng hướng, và độ dài vectơ
. Hai vectơ đó có cùng hướng, và độ dài vectơ 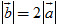 . Trong trường hợp đó ta viết
. Trong trường hợp đó ta viết 
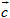 và
và 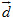 . Hai vectơ này ngược hướng, và
. Hai vectơ này ngược hướng, và 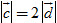 . Khi đó ta viết
. Khi đó ta viết 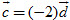 và nói rằng: Vectơ
và nói rằng: Vectơ  1. Vẽ hình bình hành ABCD.
1. Vẽ hình bình hành ABCD.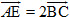 .
.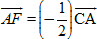 .
.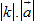 .
.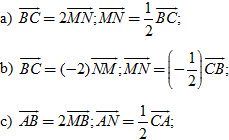


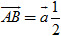 và
và 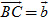 .
.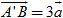 và điểm C' sao cho
và điểm C' sao cho 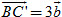 .
.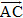 và
và 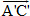 ?
?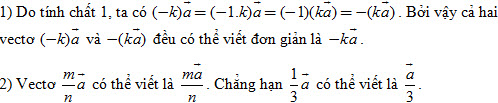
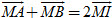 .
.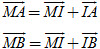
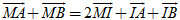
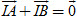 . Từ đó suy ra điều phải chứng minh.
. Từ đó suy ra điều phải chứng minh.
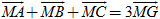

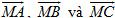 qua vectơ
qua vectơ 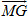 và từng vectơ
và từng vectơ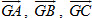 .
.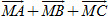 . Với chú ý rằng G là trọng tâm tam giác ABC, hãy suy ra điều phải chứng minh.
. Với chú ý rằng G là trọng tâm tam giác ABC, hãy suy ra điều phải chứng minh.
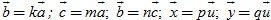 .
.
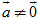 ?
?
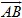 và
và 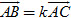 .
.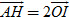 .
.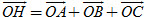 .
.
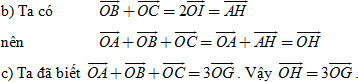
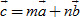 , với m và n là hai số thực nào đó, thì ta nói rằng: Vectơ
, với m và n là hai số thực nào đó, thì ta nói rằng: Vectơ 
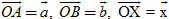 (h. 26).
(h. 26).
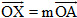 .
.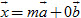 (lúc này n = 0).
(lúc này n = 0).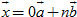 (lúc này m = 0).
(lúc này m = 0).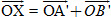 , và do đó có các số m, n sao cho
, và do đó có các số m, n sao cho 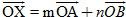 , hay
, hay 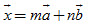
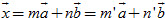 , thì
, thì 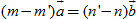 .
.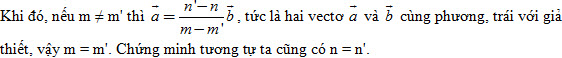
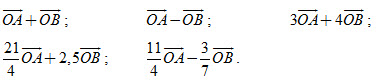
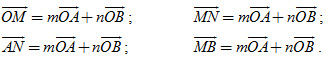
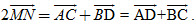
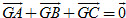 thì G là trong tâm tam giác ABC;
thì G là trong tâm tam giác ABC;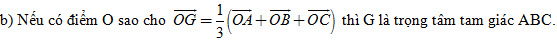
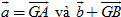 . Hãy biểu thị mỗi vectơ
. Hãy biểu thị mỗi vectơ 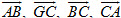 qua các vectơ
qua các vectơ 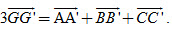
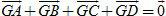 . Điểm như thế gọi là trọng tâm của bốn điểm A, B, C, D. Tuy nhiên, người ta vẫn quen gọi G là trọng tâm của tứ giác ABCD.
. Điểm như thế gọi là trọng tâm của bốn điểm A, B, C, D. Tuy nhiên, người ta vẫn quen gọi G là trọng tâm của tứ giác ABCD.




