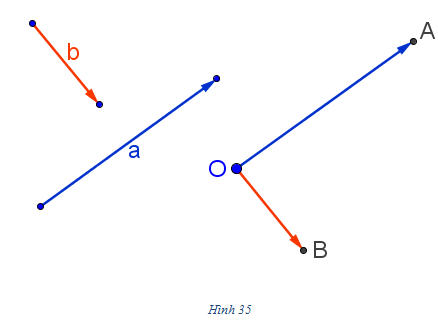
 Tải trực tiếp tệp hình học động: L10_nc_ch2_h35.ggb Xem trực tiếp hình vẽ động trên màn hình. Trong trường hợp có ít nhất một trong hai vectơ 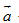 hoặc hoặc 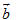 là vectơ là vectơ 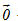 thì ta xem góc giữa hai vectơ đó là tùy ý (từ 00 đến 1800). thì ta xem góc giữa hai vectơ đó là tùy ý (từ 00 đến 1800). Rõ ràng cách xác định góc giữa hai vectơ không phụ thuộc vào việc chọn điểm O: cho nên góc giữa hai vectơ 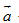 và và 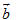 được kí hiệu là được kí hiệu là 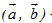 . . 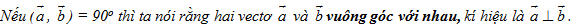 ?1. Khi nào góc giữa hai vectơ bằng 00 ? Bằng 1800 ?  1. Cho tam giác ABC vuông tại A và có 1. Cho tam giác ABC vuông tại A và có 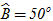 (h. 36). (h. 36).
Tính các góc 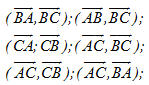
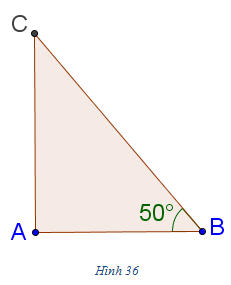 Tải trực tiếp tệp hình học động: L10_nc_ch2_h36.ggb Xem trực tiếp hình vẽ động trên màn hình. 2. Định nghĩa tích vô hướng của hai vectơ Trong Vật lí, ta có khái niệm “công sinh bởi một lực”. Giả sử một lực không đổi 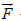 tác dụng lên một vật làm cho vật đó di chuyển từ điểm O đến điểm O’ (h. 37). tác dụng lên một vật làm cho vật đó di chuyển từ điểm O đến điểm O’ (h. 37). 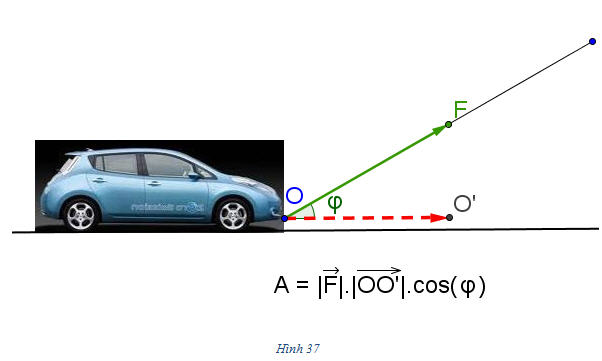 Tải trực tiếp tệp hình học động: L10_nc_ch2_h37.ggb Xem trực tiếp hình vẽ động trên màn hình. Khi đó lực 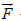 đã sinh ra một công A tính theo công thức đã sinh ra một công A tính theo công thức 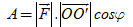
Trong đó 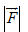 là cường độ lực là cường độ lực 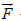 tính bằng Niutơn (kí hiệu là N), tính bằng Niutơn (kí hiệu là N), 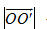 là độ dài vectơ là độ dài vectơ 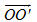 tính bằng mét (kí hiệu là m), tính bằng mét (kí hiệu là m), 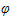 là góc giữa hai vectơ là góc giữa hai vectơ 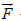 và và 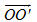 . Công A được tính bằng Jun (kí hiệu là J). Như vậy J = N. m. . Công A được tính bằng Jun (kí hiệu là J). Như vậy J = N. m. Trong Toán học, giá trị A trong các biểu thức trên (không kể đơn vị đó) được gọi là tích vô hướng của hai vectơ 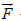 và và 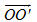 . . Tích vô hướng của hai vectơ 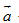 và và 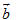 là một số, kí hiệu là là một số, kí hiệu là 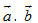 , được xác định bởi , được xác định bởi 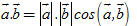 . . Ví dụ 1. Cho tam giác đều ABC có cạnh a và trọng tâm G (h. 38). Tính các tích vô hướng sau đây: 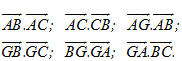
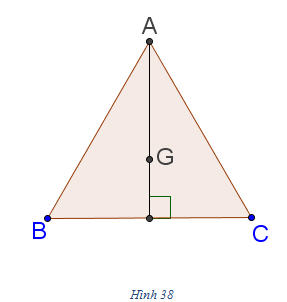 Tải trực tiếp tệp hình học động: L10_nc_ch2_h38.ggb Xem trực tiếp hình vẽ động trên màn hình. Giải. Theo định nghĩa, ta có 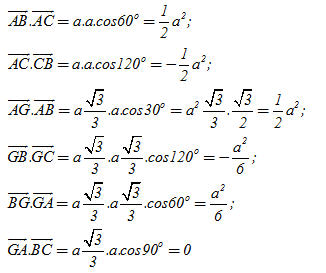
?2. Trong trường hợp nào thì tích vô hướng của hai vectơ 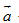 và và 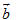 bằng 0? bằng 0? Bình phương vô hướng Với vectơ 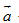 tùy ý, tích vô hướng tùy ý, tích vô hướng 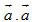 được kí hiệu là được kí hiệu là 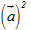 hay đơn giản hơn là hay đơn giản hơn là 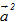 và gọi là bình phương vô hướng của vectơ và gọi là bình phương vô hướng của vectơ 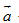 . . Từ định nghĩa của tích vô hướng ta có 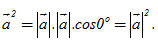
Vậy 
Hécman Grat-xơ-man (Hermann Grassmann 1808 – 1877), nhà toán học Đức, là cha đẻ của tích vô hướng của hai vectơ mà ông đã kí là 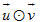 . Chính việc nghiên cứu thủy triều dẫn ông đến các khảo sát về vectơ. . Chính việc nghiên cứu thủy triều dẫn ông đến các khảo sát về vectơ. 3. Tính chất của tích vô hướng ?3. Với hai số thực a và b, ta có ab = ba. Vậy với hai vectơ 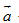 và và 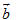 , ta có tính chất tương tự hay không? , ta có tính chất tương tự hay không? 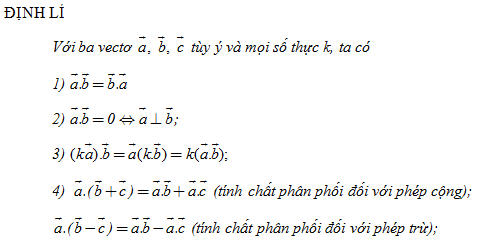
Ta có thể dễ dàng chứng minh được các tính chất 1, 2, 3. Tính chất 4 được thừa nhận, không chứng minh. Dùng các tính chất của tích vô hướng, ta có thể chứng minh các hệ thức sau: 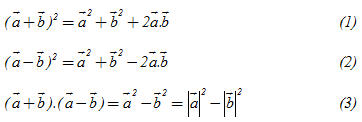
Sau đây ta chứng minh hệ thức 3. Theo tính chất phân phối ta có: 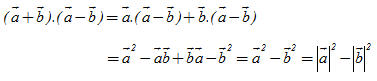
 2. Hãy chứng minh các hệ thức (1) và (2). 2. Hãy chứng minh các hệ thức (1) và (2).
?4. Ta biết rằng với hai số thực bất kì a và b, luôn có (ab)2=a2b2. Vậy với hai vectơ bất kì 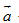 và và 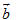 , đẳng thức có đúng không ? Viết thế nào mới đúng ? , đẳng thức có đúng không ? Viết thế nào mới đúng ? Bài toán 1. Cho tứ giác ABCD. a) Chứng minh rằng: 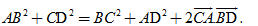
b) Từ câu a), hãy chứng minh rằng: Điều kiện cần và đủ để tứ giác có hai đường chéo vuông góc là tổng bình phương các cặp cạnh đối diện bằng nhau. Giải. (h. 39) 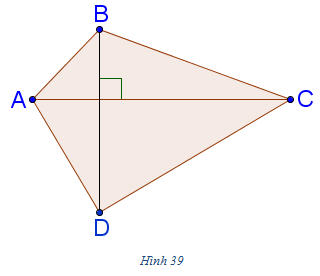 Tải trực tiếp tệp hình học động: L10_nc_ch2_h39.ggb Xem trực tiếp hình vẽ động trên màn hình. a) Ta có 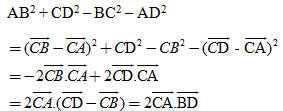
Từ đó suy ra điều phải chứng minh. b) Từ a) ta có ngay: 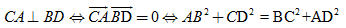
Bài toán 2. Cho đoạn thẳng AB có độ dài 2a và số k2. Tìm tập hợp các điểm M sao cho 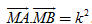 . . Giải. (h. 40) Gọi O là trung điểm đoạn thẳng AB, ta có 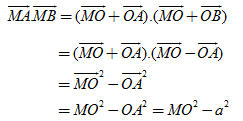
Do đó 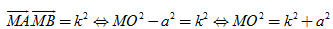
Vậy tập hợp các điểm M là đường tròn tâm O, bán kính 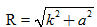 . . 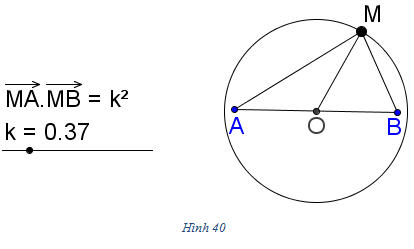 Tải trực tiếp tệp hình học động: L10_nc_ch2_h40.ggb Xem trực tiếp hình vẽ động trên màn hình. Bài toán 3. Cho hai vectơ 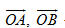 . Gọi B’ là hình chiếu của B trên đường thẳng OA. Chứng minh rằng: . Gọi B’ là hình chiếu của B trên đường thẳng OA. Chứng minh rằng: 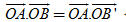 . . Chứng minh. Nếu 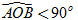 (h. 41a) thì (h. 41a) thì 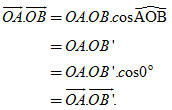
Còn nếu 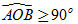 (h. 41b) thì (h. 41b) thì 
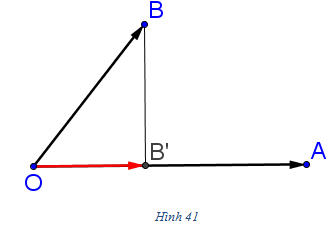 Tải trực tiếp tệp hình học động: L10_nc_ch2_h41.ggb Xem trực tiếp hình vẽ động trên màn hình. Vectơ 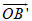 gọi là hình chiếu của vectơ gọi là hình chiếu của vectơ 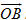 trên đường thẳng OA. trên đường thẳng OA. Công thức 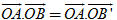 gọi là công thức hình chiếu. gọi là công thức hình chiếu.  3. Hãy phát biểu bằng lời kết luận của Bài toán 3. 3. Hãy phát biểu bằng lời kết luận của Bài toán 3.
Bài toán 4. Cho đường tròn (O;R) và điểm M cố định. Một đường thẳng Δ thay đổi, luôn đi qua M, cắt đường tròn đó tại hai điểm A và B. Chứng minh rằng: 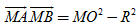
Chứng minh. (h. 42) Vẽ đường kính BC của đường tròn (O ; R). Ta có 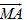 là hình chiếu của là hình chiếu của 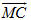 trên đường thẳng MB. Theo công thức hình chiếu, ta có trên đường thẳng MB. Theo công thức hình chiếu, ta có 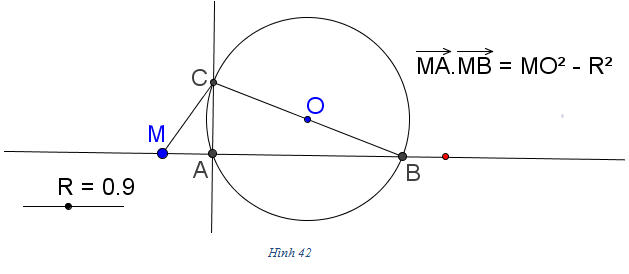 Tải trực tiếp tệp hình học động: L10_nc_ch2_h42.ggb Xem trực tiếp hình vẽ động trên màn hình. 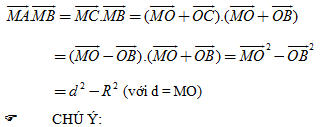
1) Giá trị không đổi 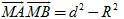 nói trong Bài toán 4 gọi là phương tích của điểm M đối với đường tròn (O) và kí hiệu là PM/(O). nói trong Bài toán 4 gọi là phương tích của điểm M đối với đường tròn (O) và kí hiệu là PM/(O). 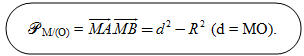
2) (h. 43) Khi điểm M nằm ngoài đường tròn (O), MT là tiếp tuyến của đường tròn đó (T là tiếp điểm), thì 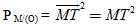
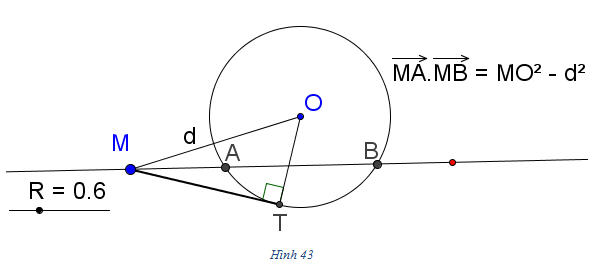 Tải trực tiếp tệp hình học động: L10_nc_ch2_h43.ggb Xem trực tiếp hình vẽ động trên màn hình. 4. Biểu thức tọa độ của tích vô hướng  4. Trong hệ tọa độ 4. Trong hệ tọa độ 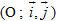 , cho , cho 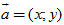 và và 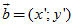 . Tính . Tính

Các hệ thức quan trọng  5. Cho hai vectơ 5. Cho hai vectơ 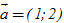 và và 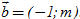
a) Tìm m để 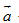 và và 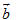 vuông góc với nhau. vuông góc với nhau. b) Tìm độ dài của 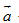 và và 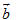 . Tìm m để . Tìm m để 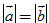 HỆ QUẢ Trong mặt phẳng tọa độ, khoảng cách giữa hai điểm M(xM ; yM) và N(xN ; yN) là 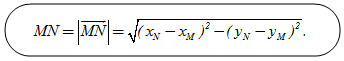
Ví dụ 2. Trong mặt phẳng tọa độ, cho hai điểm M(-2 ; 2) và N(4 ; 1). a) Tìm trên trục Ox điểm P cách đều hai điểm M, N. b) Tính cosin của góc MON. Giải. a) Vì P thuộc trục Ox nên P có tọa độ (p ; 0). Khi đó MP = NP 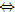 MP2 = NP2 MP2 = NP2 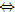 (p + 2)2 + 22 = (p – 4)2 + 12. (p + 2)2 + 22 = (p – 4)2 + 12. Từ đó ta được phương trình 12p = 9, suy ra: 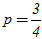 Vậy: 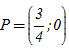
b) Ta có 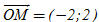 và và 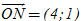 . Vậy . Vậy 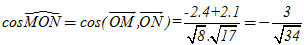
Câu hỏi và bài tập
4. Trong trường hợp nào tích vô hướng 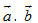 có giá trị dương, có giá trị âm, bằng 0? có giá trị dương, có giá trị âm, bằng 0? 5. Cho tam giác ABC. Tổng 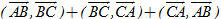 có thể nhận giá trị nào trong các giá trị sau: 900 ; 1800 ; 2700 ; 3600 ? có thể nhận giá trị nào trong các giá trị sau: 900 ; 1800 ; 2700 ; 3600 ? 6. Cho tam giác ABC vuông ở A và 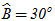 . Tính giá trị của các biểu thức sau . Tính giá trị của các biểu thức sau 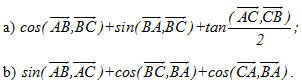
7. Cho bốn điểm bất kì A, B, C, D. Chứng minh rằng: 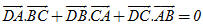
Từ đó suy ra một các chứng minh định lí: “Ba đường cao của một tam giác đồng quy”. 8. Chứng minh rằng điều kiện cần và đủ để tam giác ABC vuông tại A là 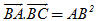
9. Cho tam giác ABC với ba đường trung tuyến AD, BE, CF. Chứng minh rằng 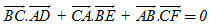
10. Cho hai điểm M, N nằm trên đường tròn đường kính AB = 2R. Gọi I là giao điểm của hai đường thẳng AM và BN. a) Chứng minh rằng: 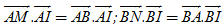
b) Tính: 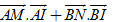 theo R. theo R. 11. Cho hai đường thẳng a và b cắt nhau tại M. Trên a có hai điểm A và B, trên b có hai điểm C và D đều khác M sao cho 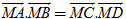 . Chứng minh rằng bốn điểm A, B, C, D cùng nằm trên một đường tròn. . Chứng minh rằng bốn điểm A, B, C, D cùng nằm trên một đường tròn. 12. Cho đoạn thẳng AB cố định, AB = 2a và một số k2. Tìm tập hợp các điểm M sao cho MA2 – MB2 = k2. 13. Trong mặt phẳng tọa độ, cho: 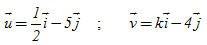
a) Tìm các giá trị của k để 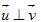 b) Tìm các giá trị của k để 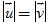 . . 14. Trong mặt phẳng tọa độ, cho tam giác ABC có các đỉnh A(- 4 ; 1), B(2 ; 4), C(2 ; -2). a) Tính chu vi và diện tích của tam giác đó. b) Tìm tọa độ của trọng tâm G, trực tâm H và tâm I của đường tròn ngoại tiếp tam giác ABC. Từ đó hãy kiểm tra tính chất thẳng hàng của ba điểm.
Schoolnet
|

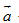 và
và 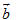 đều khác vectơ
đều khác vectơ 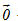 .
.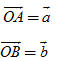

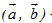 .
.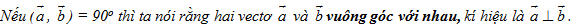
 1. Cho tam giác ABC vuông tại A và có
1. Cho tam giác ABC vuông tại A và có 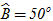 (h. 36).
(h. 36).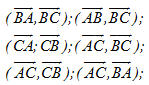

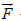 tác dụng lên một vật làm cho vật đó di chuyển từ điểm O đến điểm O’ (h. 37).
tác dụng lên một vật làm cho vật đó di chuyển từ điểm O đến điểm O’ (h. 37). 
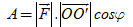
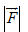 là cường độ lực
là cường độ lực 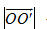 là độ dài vectơ
là độ dài vectơ 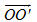 tính bằng mét (kí hiệu là m),
tính bằng mét (kí hiệu là m), 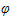 là góc giữa hai vectơ
là góc giữa hai vectơ 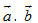 , được xác định bởi
, được xác định bởi 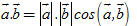 .
.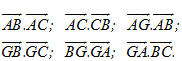

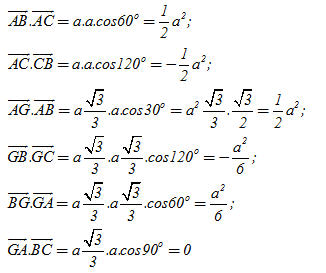
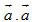 được kí hiệu là
được kí hiệu là 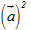 hay đơn giản hơn là
hay đơn giản hơn là 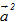 và gọi là bình phương vô hướng của vectơ
và gọi là bình phương vô hướng của vectơ 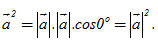

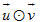 . Chính việc nghiên cứu thủy triều dẫn ông đến các khảo sát về vectơ.
. Chính việc nghiên cứu thủy triều dẫn ông đến các khảo sát về vectơ.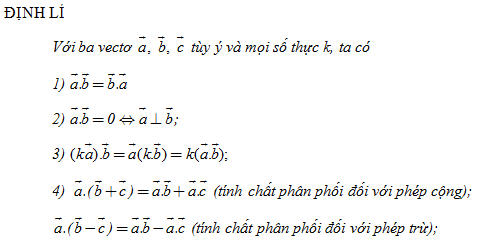
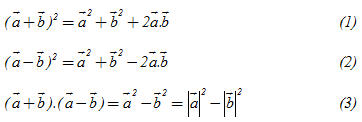
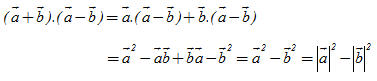
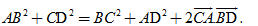

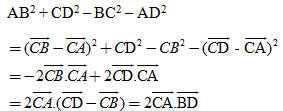
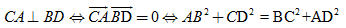
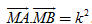 .
.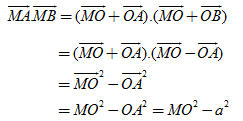
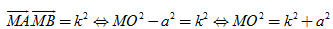
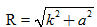 .
.
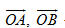 . Gọi B’ là hình chiếu của B trên đường thẳng OA. Chứng minh rằng:
. Gọi B’ là hình chiếu của B trên đường thẳng OA. Chứng minh rằng: 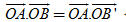 .
.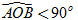 (h. 41a) thì
(h. 41a) thì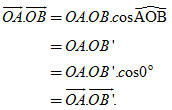
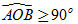 (h. 41b) thì
(h. 41b) thì

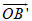 gọi là hình chiếu của vectơ
gọi là hình chiếu của vectơ 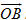 trên đường thẳng OA.
trên đường thẳng OA.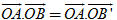 gọi là công thức hình chiếu.
gọi là công thức hình chiếu.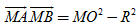
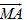 là hình chiếu của
là hình chiếu của 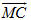 trên đường thẳng MB. Theo công thức hình chiếu, ta có
trên đường thẳng MB. Theo công thức hình chiếu, ta có
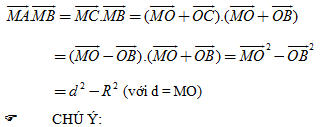
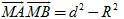 nói trong Bài toán 4 gọi là phương tích của điểm M đối với đường tròn (O) và kí hiệu là PM/(O).
nói trong Bài toán 4 gọi là phương tích của điểm M đối với đường tròn (O) và kí hiệu là PM/(O).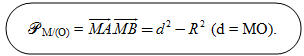
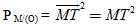

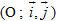 , cho
, cho 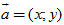 và
và 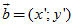 . Tính
. Tính
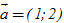 và
và 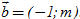
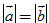
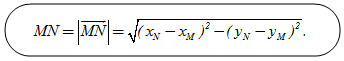
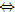 MP2 = NP2
MP2 = NP2 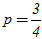
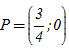
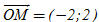 và
và 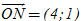 . Vậy
. Vậy 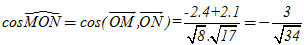
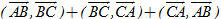 có thể nhận giá trị nào trong các giá trị sau: 900 ; 1800 ; 2700 ; 3600 ?
có thể nhận giá trị nào trong các giá trị sau: 900 ; 1800 ; 2700 ; 3600 ?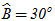 . Tính giá trị của các biểu thức sau
. Tính giá trị của các biểu thức sau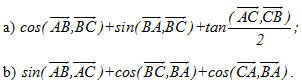
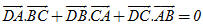
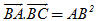
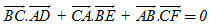
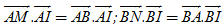
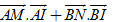 theo R.
theo R.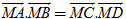 . Chứng minh rằng bốn điểm A, B, C, D cùng nằm trên một đường tròn.
. Chứng minh rằng bốn điểm A, B, C, D cùng nằm trên một đường tròn.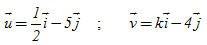
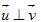
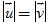 .
.




