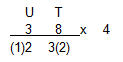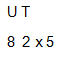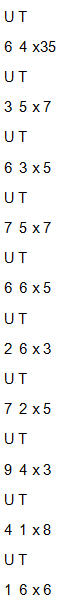Trước hết, chúng ta sẽ nhìn vào các tính năng mới được thêm vào phương pháp, và sau đó chúng ta sẽ áp dụng nó vào vấn đề cần giải quyết để có thể giải quyết triệt để về phép nhân. Do vậy bây giờ chúng ta hãy tạm quên phương pháp nhân mà chúng ta đang áp dụng và chỉ tập trung vào những điểm sau: 1. Một chữ số là một số có một chữ số, như 5 hoặc 7. 0 cũng là một chữ số. 2. Khi chúng ta nhân một chữ số với một chữ số, chúng ta nhận được một số có một hoặc hai chữ số. Chứng minh: kết quả lớn nhất mà chúng ta có thể nhận được là 9 nhân 9 bằng 81, là số có hai chữ số. 3. Đôi khi chúng ta nhân một chữ số với một chữ số, tạo thành kết quả có một chữ số, dạng như 2 nhân 3. Khi đó ta vẫn xét đến nó như một số có hai chữ số bằng cách viết thêm một số 0 nữa ở trước nó. Ta sẽ nói, trong phương pháp sẽ trình bày, 2 nhân 3 bằng 06. Nó sẽ giúp ích cho việc đơn giản hóa các quy tắc và thủ tục thực hiện, bằng cách chuẩn hóa tất cả các kết quả thành số có hai chữ số. Tất nhiên, viết một số 0 ở đằng trước kết quả, không làm thay đổi giá trị thực của nó. 4. Trong các số có hai chữ số, chữ số hàng bên trái là hàng “chục”, chữ số còn lại là hàng “đơn vị”. Lấy ví dụ, trong số 37, hàng chục là 3 và hàng đơn vị là 7. Nó được áp dụng rộng rãi trong cuộc sống hàng ngày, bởi vì nếu chúng ta có 37 $, chúng ta có tương ứng biểu diễn 3 chục và 7 đơn vị, không có biểu diễn nào khác. 5. Trong phương pháp mới, chúng ta sẽ thường xuyên chỉ làm việc với chữ số hàng đơn vị của một số. Lấy ví dụ, chúng ta có thể đi qua số 24 và chỉ xem là “4”, mà không cần đến số 2 ở hàng chục. Bạn có thể cho rằng là sai, vì bỏ qua số hàng chục. Tuy nhiên, nó vẫn đúng bởi vì số hàng chục bị quên sẽ được tính vào một hàng nào đó của kết quả. Trong một số trường hợp khác, chúng ta chỉ sử dụng số hàng chục mà bỏ qua số hàng đơn vị. Trong trường hợp này chúng ta nhìn số 24 và chỉ quan tâm đến số 2. 6. ĐIỀU NÀY RẤT QUAN TRỌNG. Trong phương pháp mới chúng ta thường xuyên phải kết hợp điều 2 và điều 5. Do vậy khi nói, trong phép nhân hai chữ số lại với nhau, như 3 nhân 8, chúng ta thường sử dụng hàng đơn vị của kết quả, ví dụ số 4 của 24, hoặc trong một vài trường hợp khác, chỉ dùng đến chữ số hàng chục, như số 2 ở kết quả trên. Đó là một phương pháp nhân nhẩm hơi lạ. Chúng ta không xem nó như phép nhân thông thường, và bạn có thể bỡ ngỡ vài lần đầu khi áp dụng nó. Hãy nhìn các ví dụ sau và đọc nhẩm với chỉ hàng đơn vị của kết quả: 
Kết quả: 2, 8, 0 và 6. Bây giờ xem lại các ví dụ trên và hãy nhẩm hàng chục của kết quả. Kết quả: 1, 1, 2 và 1. 7. Bây giờ chúng ta hãy xem xét đến ý nghĩa tên của phương pháp “hàng chục và hàng đơn vị”. Đặt hai chữ số lại gần nhau, như 3 và 8. Nhân mỗi số với các chữ số khác, như 4, sử dụng ý tưởng về chỉ lấy kết quả hàng đơn vị và hàng chục của kết quả, như chúng ta đã làm ở bước 5. Tất nhiên, chúng ta sẽ làm theo một cách đặc biệt. Chúng ta chỉ sử dụng chữ số hàng đơn vị khi nhân chữ số hàng bên trái (3) và hàng chục của phép nhân chữ số hàng bên phải (8). Kí hiệu U mang ý nghĩa chúng ta chỉ giữ chữ số hàng đơnvij của kết quả, kí hiệu T mang ý nghĩa chúng ta chỉ giữ chữ số hàng chục. Kết quả, được viết trong cặp dấu ngoặc là” 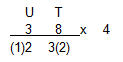
Chúng ta sẽ luôn dùng kí hiệu U và T theo thứ tự trên từ bây giờ. Với chữ số bên trái của cặp số đối diện, như số 3 của 3 8, chúng ta chỉ dùng hàng đơn vị của kết quả. Cho chữ số hàng bên phải của cặp số, số 8 của 3 8, chúng ta chỉ sử dụng chữ số hàng chục của kết quả. 8. Cuối cùng, chúng ta thực hiện thêm một bước đơn giản – chúng ta cộng hai kết quả đã nhận được ở bước 7. Chúng ta có 2 và 3, cộng lại được 5. Đó là kết quả mà ta sẽ dùng trong quá trình nhân thực sự.Để ý rằng chúng ta chỉ nhận được một chữ số 5, từ cặp số 3 và 8. Chúng ta “nhân“ 3 8 với 4, tuy nhiên nó không phải là phép nhân thông thường. Đó là thuộc tính của phương pháp “hàng chục và hàng đơn vị”; một cặp số được nhân bởi chữ số thé ba và bạn kết thúc với việc chỉ nhận được một chữ số kết quả. Điều xảy ra trong trường hợp này là chúng ta chỉ cần chữ số hàng đơn vị và hàng chục của các kết quả. Bởi vì đây là một phần thiết yếu của “phương pháp hai ngón tay”, chúng ta sẽ trình bày ví dụ đầy đủ hơn. Chúng ta sử dụng lại ví dụ 3 8 nhân 4 (phép nhân không theo nghĩa thông thường), và chúng ta sẽ trình bày theo sơ đồ sau: 
Chúng ta phải nhấn mạnh lại rằng đây chưa phải là một áp dụng trong thực tế, sau khi phương pháp đã trở nên quen thuộc, ta không cần phải viết dạng đầy đủ như thế này. Không có số nào được viết ngoại trừ những số được tính, là 3, 8 và 4, và kết quả là 5. Hơn thế nữa: sau khi bạn đã nắm được phương pháp bạn nên tránh đến việc nghĩ về cách tínhcác số trung gian bạn nhìn thấy trong sơ đồ. Nó lên được thực hiện một cách thức tự động, phần lớn những số liên quan sẽ tiếp tục được tính trong đầu bạn. Bạn nhìn cặp 3 8 và 4 và sau đó nên để tâm đến các số 2 và 3 (trong 12 và 32), sau đó đọc nhẩm 5 một cách tức thì. Mức độ thực hiện tốt sẽ đến sau một số lần thực hiện, như đã làm trong các phương pháp trước. Để nhấn mạnh về sự quan trọng của quá trình ta đang thực hiện, chúng ta gọi kết quả quá trình tính này theo một cái tên đặc biệt, “cặp kết quả”. Số 5 chúng ta nhận được từ ví dụ trên là “cặp kết quả” của 3 8 X 4 Định nghĩa: Một cặp kết quả là một số nhận được bằng cách nhân một cặp các chữ số bởi các chữ số được phân cách trong số nhân theo một cách đặc biệt: chúng ta sử dụng các chữ số của số nhân để nhân mỗi chữ số trong cặp một cách tách biệt, và sau đó chúng ta cộng lại các số hàng đơn vị của kết quả phép nhân các chữ số hàng bên trái và hàng chục của kết quả nhân các chữ số bên phải trong cặp. Chữ số mà ta nhận được theo cách này, cặp kết quả, được chúng ta sử dụng trong phép nhân nhanh vì chúng cho phép chúng ta thực hiện phép nhân mà không phải nhớ với số lớn, hoặc phải làm việc với những số lớn. Chúng ta sẽ thấy tác dụng của nó ngay bây giờ. Đầu tiên chúng ta xem một số ví dụ trong đó có một số điều nhỏ cần chú ý: 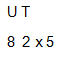
Kết quả là 1, như bạn có thể tính nhẩm, nếu không, bạn có thể xem lại cách thực hiện: 
Chúng ta cộng hai chữ số này lại với nhau để nhận được cặp kết quả. Có một số trường hợp chúng ta nhận được kết quả vượt quá 10, như 11 trong ví dụ cuối. Nhưng để ý rằng, nó không bao giờ vượt quá 18, do đó chúng ta chỉ cần đánh một dấu chấm cho nó. Những điều được minh họa trong các ví dụ cần được chú ý: 1. Hãy cố nghĩ về các kết quả có một chữ số như một số có hai chữ số nếu nó có số 0 được viết ở đằng trước. Ví dụ, 2 nhân 2 là 04, 6 nhân 1 là 06. Mục đích của việc làm này để giúp bạn có ý thức tránh lỗi xảy ra. Hãy nghĩ nhanh về chữ số hàng chục của phép nhân 2 với 2, chúng ta có thể nhận nhầm là 4. 2. Khi chúng ta cộng hai phần kết quả, hàng chục của một số và hàng đơn vị của số còn lại, kết quả nhận được có thể vượt quá 10, do đó ta có thể nhận được số có hai chữ số. Trong trường hợp này, chúng ta làm như thông thường, viết lại hàng đơn vị và đánh dấu hàng chục bởi một dấu chấm. Nó có ý nghĩa rằng chúng ta đang làm việc với số nhớ, tuy nhiên rất dễ nhớ. Chúng ta sẽ không cần cộng đến số nhớ 15, như chúng ta đã thấy trong chương trước. 3. Hãy nhớ, 0 nhân với bất cứ số nào cũng là 0, và nhân bất cứ số nào với 1 cũng không làm thay đổi giá trị của nó. 4. Chỉ có 1 hoặc 2 quá trình tính cặp kết quả nên được viết ở dạng đầy đủ, như chúng ta đã làm ở phần trước. Sau khi bạn đã viết một hoặc hai sơ đồ, bạn nên cố gắng tập trung để hình dung hai số trong cặp – như 12 và 32, và kết hợp các chữ số bên trong của chúng (để nhận được 5). Nó rất dễ để bạn hình dung. Điều quan trọng là bạn phải tập thói quen bỏ qua một số bước – có nghĩa là bạn thực hiện một số bước tính toán mà không cần tập trung vào nó. Thực hành một số lần đủ để bạn làm được điều này.một số lần đủ để bạn làm được điều này. Hãy thử làm thêm một số ví dụ sau để thực hành: 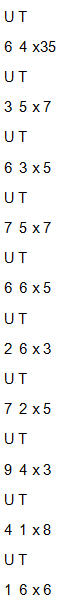
Tạm ngừng một chút. Nếu mọi việc đều hoàn hảo, bạn có thể tiếp tục với phần sau. Nếu không, hãy quay lại và thử làm lại. Đây là một khâu rất quan trọng, tuy rằng nó không phức tạp, do đó bạn cần phải nắm vững. Đó là khâu quan trọng nhất trong chương này.
School@net
|

 Như ta đã thấy ở chương trước, một tiện ích quan trọng của hệ thống tính toán Trachtenberg là chúng ta có thể nhân bất cứ hai số nào và viết ra kết quả một cách trực tiếp. Chúng ta không viết các phép tính trung gian như cách làm thông thường. Phương pháp trực tiếp chúng ta vừa học là một trong những áp dụng có tính tổng quát – nó có thể được dùng để nhân hai số bất kỳ với nhau. Nhưng trong nhiều trường hợp, nó cần thêm những cải tiến phù hợp. Khi chúng ta áp dụng phương pháp đó với những số có nhiều chữ số có giá trị lớn, như 978 nhân 647, chúng ta sẽ phải cộng lại các kết quả lớn trong đầu, và phải nhớ những số nhớ lớn. Phát triển tiếp theo cho phương pháp bao gồm việc giảm bớt việc tính toán những số lớn trong đầu. Chúng ta thực hiện điều này bằng việc tích hợp vào phương pháp một bước mới – mà giáo sư Trachtenberg gọi là phương pháp “hai ngón tay”. Nó cũng có thể giống với phương pháp được gọi “các số hàng đơn vị và các số hàng chục”. Bạn sẽ biết rõ hơn về các tên này và các phương pháp trên, ở phần sau.
Như ta đã thấy ở chương trước, một tiện ích quan trọng của hệ thống tính toán Trachtenberg là chúng ta có thể nhân bất cứ hai số nào và viết ra kết quả một cách trực tiếp. Chúng ta không viết các phép tính trung gian như cách làm thông thường. Phương pháp trực tiếp chúng ta vừa học là một trong những áp dụng có tính tổng quát – nó có thể được dùng để nhân hai số bất kỳ với nhau. Nhưng trong nhiều trường hợp, nó cần thêm những cải tiến phù hợp. Khi chúng ta áp dụng phương pháp đó với những số có nhiều chữ số có giá trị lớn, như 978 nhân 647, chúng ta sẽ phải cộng lại các kết quả lớn trong đầu, và phải nhớ những số nhớ lớn. Phát triển tiếp theo cho phương pháp bao gồm việc giảm bớt việc tính toán những số lớn trong đầu. Chúng ta thực hiện điều này bằng việc tích hợp vào phương pháp một bước mới – mà giáo sư Trachtenberg gọi là phương pháp “hai ngón tay”. Nó cũng có thể giống với phương pháp được gọi “các số hàng đơn vị và các số hàng chục”. Bạn sẽ biết rõ hơn về các tên này và các phương pháp trên, ở phần sau.