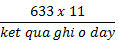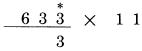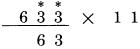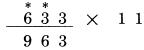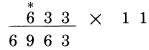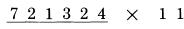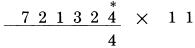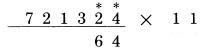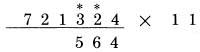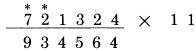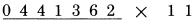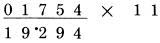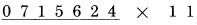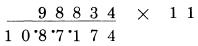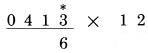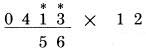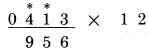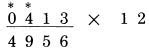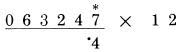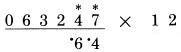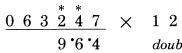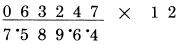Để giải thích rõ hơn điều này, cần nói rõ: chúng ta không nói sẽ bỏ qua bảng nhân. Phần lớn mọi người biết sự hữu dụng của nó trong thực tế, ngoại trừ một số ngoại lệ khó khăn khi áp dụng. Việc thực hiện tám nhân với bẩy, hoặc sáu nhân với chín có thể không chắc chắn với nhiều người, tuy nhiên tính toán với các số nhỏ hơn như bốn nhân năm gần như là một câu lệnh chính xác trong não người. Chúng ta áp dụng việc sử dụng các hiểu biết có sẵn này. Cái chúng ta hướng đến là sử dụng hiệu quả chúng. Phần cuối chương này chúng ta sẽ quay lại vấn đề này. Bây giờ chúng ta cần học cách nhân mà không cần sử dụng một bảng nhân nào cả. Bây giờ chúng ta xem xét phép nhân với 11. Để tiện lợi cho việc giải thích, chúng ta sẽ phát biểu phương thức nhân theo mẫu các quy tắc sau: PHÉP NHÂN VỚI 11: 1.Chữ số cuối của số bị nhân được đặt chính xác tại vị trí bên phải nhất của tích. 2.Mọi chữ số của số bị nhân được cộng với số liền kề với nó bên tay phải. 3.Chữ số đầu tiên của số bị nhân trở thành số bên trái nhất của tích. Đó là bước cuối cùng của phép tính. Trong cách tính Trachtenberg, bạn hình dung kết quả một lần tại mỗi thời điểm, từ phải qua trái, đúng như cách bạn làm theo từng bước như sau: Lấy 1 ví dụ đơn giản: 633 nhân 11 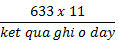 Kết quả sẽ được ghi dưới số 633, được tính theo từng bước, từ phải sang trái sau khi chúng ta áp dụng các quy tắc ở trên. Chúng ta sẽ biểu diễn việc tính toán theo mẫu dưới. Dấu sao (*) ở trên số bị nhân được dùng để chỉ rõ từng chữ số ta sẽ áp dụng trong từng bước. Áp dụng quy tắc đầu tiên: Viết chữ số cuối cùng của số 633 về bên phải của hàng kết quả như sau: 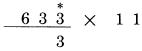 Áp dụng quy tắc thứ hai: Mỗi chữ số các hàng còn lại của số 633 được cộng với chữ số hàng bên phải liền kề với nó: 3 cộng 3 bằng 6 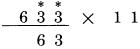
Áp dụng quy tắc trên một lần nữa, 6 cộng 3 bằng 9 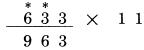 Áp dụng quy tắc thứ ba: Chữ số đầu tiên của 633, số 6 trở thành chữ số bên trái nhất của kết quả: 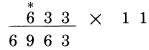
Kết quả là 6,863. Việc tính toán với những số có độ dài lớn hơn cũng được thực hiện theo cách tương tự. Quy tắc thức hai, “mỗi chữ số của các hàng còn lại của số bị nhân được cộng với số bên phải của nó”, được sử dụng hai lần trong ví dụ trên, ở các phép tính khác có thể được áp dụng nhiều hơn. Lấy ví dụ 721,324 nhân 11: 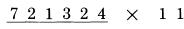 Áp dụng quy tắc một: Chữ số cuối cùng của 721,324 được viết ở vị trí bên phải nhất của kết quả: 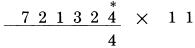 Áp dụng quy tắc thứ hai: Mỗi hàng còn lại của 721,324 được cộng với số bên phải nó: 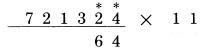
2 cộng 4 là 6 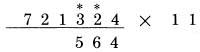 3 cộng 2 là 5  1 cộng 3 là 4  2 cộng 1 là 3 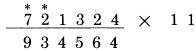 7 cộng 2 là 9 Áp dụng quy tắc thứ ba: Chữ số hàng đầu tiên của 721,324 trở thành số hàng đầu tiên của kết quả: 
Kết quả là 7,934,564. Như bạn đã thấy, ở mỗi ví dụ mỗi chữ số mỗi hàng được dùng hai lần. Một lần dùng để như một chữ số gốc, và sau đó,ở lần tiếp theo được dùng như một chữ số liền kề. Ở ví dụ trên, chữ số 1 (của số bị nhân) được dùng như phần số gốc khi nó tạo số 4 ở chữ số cùng hàng tại kết quả, và có vai trò như một số liền kết khi nó tạo số 3 ở hàng bên trái phía trước.  Thay vì áp dụng đủ 3 quy tắc, chúng ta có thể chỉ dùng một quy tắc: “cộng với số liền kề” nếu chúng ta áp dụng trong tính toán hàng ngày, tạo một thói quen áp dụng hiệu quả Chúng ta cần viết số 0 ở phía các hàng, hoặc ít nhất tưởng tượng có một số 0 ở đây. Sau đó, chúng ta áp dụng quy tắc cộng số liền kề tại mỗi hàng của kết quả, có dạng:  Ví dụ trên chỉ ra tại sao chúng ta sử dụng số 0 ở phía trước số bị nhân. Chúng giúp chúng ta tạo được phép tính liền mạch, không cần dừng lại. Nếu bỏ số 0 ở đầu đi, chúng ta phải mất thời gian xao nhãng để quan tâm đến số 6 cuối cùng, và chúng ta có thể nghĩ rằng kết quả là 963. Đáp án dài hơn kết quả nhận được một chữ số, và số 0 ở đầu giúp chúng ta xử lý vấn đề này. Thử với phép tính: 441,362 nhân 11. Chúng ta viết lại theo mẫu: 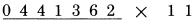 Nếu chúng ta bắt đầu với số 2, là số bên phải nhất để bắt đầu, và tiếp tục công việc về phía trái, cộng các hàng với số liền cạnh trong mỗi lần, chúng ta kết thúc với đáp án chính xác: 4.854,882. Đôi khi bạn sẽ cộng một số với số cạnh nó và nhận được một kết quả có hai chữ số, như 5 cộng 8 ra kết quả 13. Trong trường hợp này, bạn viết số 3 và “nhớ” số 1, để tiếp tục chuyển lên các hàng cao hơn. Tuy nhiên bạn sẽ thấy trong phương pháp của Trachtenberg, bạn sẽ không cần phải nhớ với một số lớn. Nếu có phép nhớ, nó chỉ là 1, hoặc trong các phép tính tiếp theo có thể là 2. Nó tạo nên sự khác biệt đáng kể khi chúng ta làm việc với các phép tính phức tạp. Để cho tiện biểu diễn, chúng ta đáng một dấu chấm cho số nhớ 1, và dấu hai chấm cho số nhớ 2: 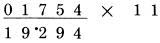
- 2 của 12 từ tổng 7 cộng 5 Bạn hãy thử với phép tính: 715,624 nhân 11. Viết nó dưới dạng: 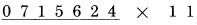
Ở đây có nhớ 1 hàng số 4 của số nhân. Kết quả chính xác là 7,871,864. Trong trường hợp đặc biệt, với các số lớn bắt đầu bởi chữ số 9 theo sau bởi 1 chữ số lớn, ví dụ như số 8, chúng ta có thể nhận được kết quả 10 ở bước cuối cùng. Lấy ví dụ: 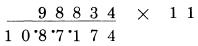 PHÉP NHÂN VỚI MƯỜI HAI Để thực hiện phép nhân với 12, chúng ta làm như sau: Gấp đôi mỗi chữ số ở số bị nhân và cộng nó với số bên cạnh. Việc thực hiên cũng tương tự như phép nhân với 11 ngoại trừ rằng bây giờ chúng ta cần phải gấp đôi mỗi chữ số trước khi cộng nó với số bên cạnh. Nếu chúng ta muốn nhân 413 với 12, chúng ta làm như sau: Bước 1: gấp đôi chữ số ngoài cùng bên phải và viết xuống hàng dưới (không có chữ số liền kề) 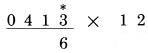
Bước 2: gấp đôi 1 và cộng 3 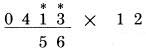
Bước 3: gấp đôi 4 và cộng 1 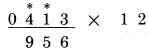
Bước cuối: gấp đôi 0 được 0 và cộng 4 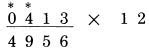 Đáp án là 4,956. Nếu bạn thực hiện đủ các bước, bạn sẽ thấy rằng việc thực hiện rất nhanh và dễ dàng. Thử một ví dụ khác: 63.247 nhân với 12. Viết phép tính với các chữ số đặt cách nhau, và đặt mỗi chữ số của kết quả ngay dưới các chữ số của số 63,247 theo thứ tự xuất hiện của chúng. Đó không chỉ là một thói quen tốt vì sự gọn gàng, mà còn có giá trị ngăn ngừa lỗi. Trong trường hợp áp dụng cụ thể, chúng ta cần lưu ý điều này, để định vị trí các số và số liền kề. Ô trống bên cạnh kết quả, nơi chữ số tiếp theo của kết quả được viết trực tiếp bên dưới chữ số (là số mà bạn cần phải nhân lên với 2). Chữ số ở vị trí bên phải trở thành số bên cạnh để cộng vào. Ta lấy một ví dụ: gấp đôi 7, được 14, nhớ 1 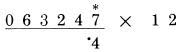
gấp đôi 4, cộng 7, cộng 1 được 16; nhớ 1 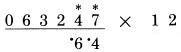
gấp đôi 2, cộng 4, cộng 1 được 9 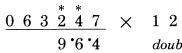
Cho đến khi ta kết thúc: 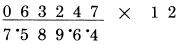
Còn tiếp ...
School@net (Theo NamTB)
|

 CÁC PHÉP NHÂN CƠ BẢN
CÁC PHÉP NHÂN CƠ BẢN