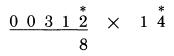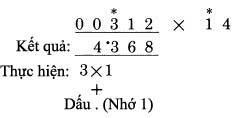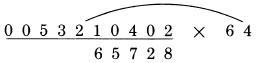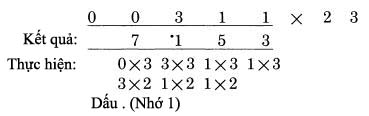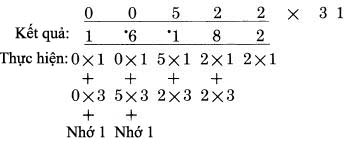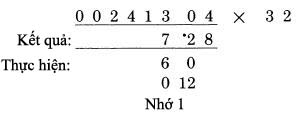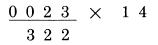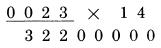Bước 1: Nhân hai hàng bên phải nhất của hai số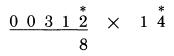

Bước 2: Bây giờ sử dụng các cặp số bên trong và bên ngoài. Chữ số tiếp theo ta làm việc là số 1 của 312. Đó là vị trí hàng kết quả sẽ được tính. Do đó 1 là một phần của cặp số ngoài.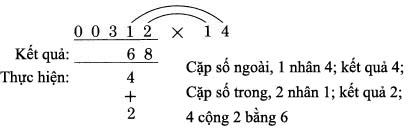

Bước 3: Thực hiện lại bước 2, ngoại trừ việc chúng ta phải dịch chuyển các cặp số. Do đó, chúng ta có các cặp số khác. Nhưng vẫn theo quy tắc trước, chữ số tiếp theo của 312 là chữ số ngay trên hàng kết quả cần điền, đó là một phần của cặp số ngoài. Trong ví dụ này, đó là số 3. Do đó ta có: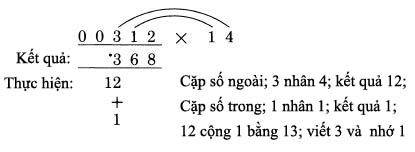

Bước cuối cùng: Để tìm chữ số hàng bên trái nhất của kết quả, nhân hai chữ số ngoài cùng bên trái, 3 với 1 và cộng thêm nhớ 1: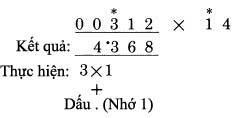

Tiếp theo chúng ta sẽ cần mở rộng các đường cong kết nối quá số 0 ở đằng trước số bị nhân. Bây giờ chúng ta thực hiện điều đó ở đây, để làm rõ việc thực hiện như thế nào. Nhớ rằng:

BẤT CỨ SỐ NÀO NHÂN VỚI 0 CŨNG LUÔN RA KẾT QUẢ LÀ 0

Trong phép nhân, số 0 luôn triệt tiêu kết quả với mọi số khác. Một triệu nhân 0 cũng ra 0. Sử dụng hệ quả này, chúng ta thực hiện bước cuối như thực hiện với các bước trung gian.

Bước cuối: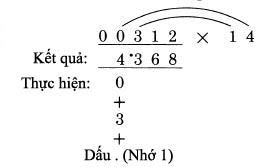

Cặp số ngoài, 0 nhân 4, được kết quả 0. Cặp số bên trong, 3 nhân 1, được 3. Tổng hai cặp, 0 cộng 3 là 3. Thêm các số nhớ (dấu .) ta nhận 4, kết quả giống với kết quả ta làm ở trước. Điều này chứng tỏ chúng ta có thể thực hiện bước cuối tương tự như bước hai và bước ba, đó là chúng ta vẫn thực hiện qua cặp số trong và ngoài, thay vì sử dụng một quy tắc riêng ở bước cuối.

Mỗi lần chúng ta thể hiện hàng kết quả và đánh dấu nó “làm việc”, nó được hiểu rằng trong thực tế ta sẽ thực hiện nó bằng cách tính nhẩm trong đầu. Chúng ta đã thể hiện các bước làm việc một cách tường minh chỉ để mục đích giải thích. Khi bạn làm việc thực sự, bạn chỉ việc thực hiện nó bằng cách viết hai chữ số mà bạn muốn nhân và kết quả đem lại.

Ví dụ chúng ta sẽ trình bày dưới đây trình bày cách định vị vị trí cặp số bên ngoài. Nó luôn luôn được xác định bởi hệ quả: phải bao gồm chữ số của số bị nhân trực tiếp nằm trên vị trí hàng kết quả sẽ được tính: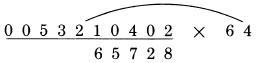

Chiều còn lại của đoạn thẳng nối với phần bên tay phải của số nhân có hai chữ số, bởi vì đó là vị trí nằm ngoài. Sau đó cặp số bên trong được lấy từ hai chữ số ngay cạnh phía trong cặp số ta đang sử dụng.

Trong thực tế, có thể bạn sẽ thấy rằng có một cách hay để làm điều này, để đánh dấu vị trí của các chữ số trong cặp số trong và cặp số ngoài, bằng việc chỉ lại vị trí các cặp số với ngón tay của bạn. Nó không quá đối rắc tối, vàngăn ngừa các lỗi có thể xảy ra từ việc để quên vị trí hiện thời của các số. Trong trường hợp nhân số có ba chữ số với số có hai chữ số, như 312 nhân 14, nguy cơ này là khôn lớn, nhưng chúng ta sẽ thấy trong các trường hợp dài hơn. Trong bất cứ trường hợp nào, một lời khuyên là bạn nên viết các chữ số rõ ràng và ngăn cách nhau, và viết các chữ số hàng kết quả ngay dưới vị trí của số hàng nhân nó làm việc. Sự gọn gàng sẽ giúp tránh các lỗi không cần thiết. Nó không chỉ giúp chúng ta trong phương pháp này, mà còn trong cả các phép tính cộng trừ, hoặc nhân theo phương pháp thông thường. Sự gọn gàng là thói quen tốt cần phát triển.

Đây là cách để bạn tự kiểm tra mình xem đã hiểu về phương pháp này nhưn thế nào. Bên dưới là ví dụ hoàn chỉnh của phép nhân 311 với 23. Kết quả được viết dưới số 311, và hàng làm tính nhân, giả sử đã có trong đầu bạn, sẽ được viết dưới kết quả. Bây giờ chúng ta viết lại cả hàng kết quả và hàng nhân trên giấy, và tính lại hàng bên phải của kết quả trong đầu. Dịch chuyển tờ giấy đủ xa để nhìn được hàng đầu của kết quả, và bạn sẽ biết mình có làm đúng hay không. Sau đó tính nhẩm các hàng tiếp theo của kết quả, khi bạn có nó, dịch lại tờ giấy để đối chiếu xem bạn có làm đúng hay không ? Nếu bạn làm sai, xem kỹ lại hàng nhân để biết về chữ số đó, và bạn sẽ thấy nó được tính như thế nào. Trong các bước làm việc, mỗi hàng được cộng với nhau để tạo chữ số của hàng kết quả.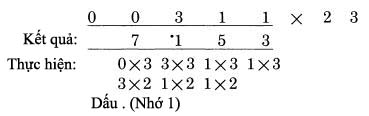

Những số 0 ở đầu

Trong ví dụ trên chúng ta đã nhìn thấy, chúng ta có hai số 0 ở đằng trước số bị nhân, nhưng chỉ một số được dùng. Thỉnh thoảng, trong trường hợp khác chúng ta có hai chữ số ở hàng trước. Xem xét ví dụ sau: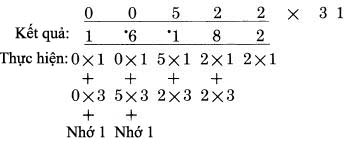

Trong trường hợp này chúng ta có chữ số ở dưới số 0 thứ hai, khi thực hiện đến bước cuối. Chú ý rằng đó chỉ là kết quả của việc nhớ 1 (dấu .). Các chữ số của 31 không đem lại kết quả, vì chúng đều bị triệt tiêu khi nhân với 0. Chỉ duy nhất số nhớ còn lại.

Điều này giải thích tại sao chúng ta cần tới hai chữ số 0 ở đằng trước. Một chữ số 0 ở đằng trước số bị nhân cũng có kết quả tương tự, khi không cần cộng nhớ ở bước cuối cùng.

Quy tắc tổng quát: Khi nhân với số nhân có độ dài bất kỳ, đặt số số 0 ở đằng trước số bị nhân trong khoảng từ 1 cho tới số chữ số của số nhân.

Thỉnh thoảng, như ta đã thấy, chúng ta không cần dùng hết các số 0, tuy nhiên làm theo quy tắc này không gây bất cứ thiệt hại nào. Nếu chúng ta áp dụng quy tắc và sử dụng hai số 0thay vì chỉ cần một số 0, chúng ta sẽ thấy hiển nhiên bước cuối không cần thực hiện.

Với những số có nhiều chữ số, như 241,304 cũng được xử lý như trên. Chúng ta đơn giản chỉ lặp lại việc nhân các cặp số lại với nhau và tính tổng. Giả sử bạn muốn nhân 241,304 với 32: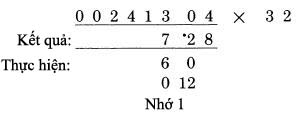

Đây là trường hợp mở rộng hơn so với các ví dụ trước vớisố có 3 chữ số là số bị nhân. Bước tiếp theo được hoàn thành theo phương pháp cũ: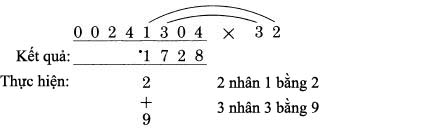

Tất nhiên, chúng ta cộng 2 và 9, ra 11 là chữ số tiếp theo của kết quả. Ta viết 1 là một phần kết quả và nhớ 1 bằng cách đánh dấu (.). Sau đó ta tiếp tục dịch sang trái. Cặp số tiếp theo được xác định là (4,1) và (3,2) đưa ra kết quả là 4 nhân 2 cộng 1 nhân 3. Cách giải hoàn chỉnh như sau:

Số 0 ở vị trí xa nhất không được dùng. Đó là một trường hợp khi không có nhớ ở bước cuối, do vậy ta không cần gi dưới số 0 cuối cùng. Chúng ta biểu diễn nó chỉ với mục đích hoàn thiện các bước. Quy tắc áp dụng với việc gi 2 số 0 ở đầu tương ứng với 2 chữ số nhân. Một số 0 bị bỏ phí nhưng toàn cục, nó không có giá trị gì.

Sau đây là một chút thủ thuật nhỏ “tư duy - vấn đề” : Bạn nên tự trả lời nó mà không cần thực hiện tính toán trực tiếp. Bây giờ bạn đã biết, kết quả của 311 nhân 23 là 7,153, vậy kết quả của phép nhân 31,100 với 23 ? Khác biệt duy nhất là bây giờ ta có hai số 0 ở đằng sau số bị nhân. Vậy kết quả bây giờ là gì ? Quyết định trước khi bạn đọc tiếp đoạn sau.

Kết quả, không còn nghi ngờ gì nữa là 715,300. Hai số 0 mở rộng đằng sau số bị nhân đưa lại kết quả 2 số 0 tương ứng sau kết quả. Điều này luôn luôn đúng. Bất kỳ số 0 nào được viết sau số bị nhân, không cần biết số bị nhân là bao nhiêu – sẽ được gi tương ứng vào sau kết quả.

Có bốn cách giải có thể để bạn có thể áp dụng trong trường hợp này. Có thể bạn rất thông minh để sử dụng nhiều hơn một cách tại cùng một lúc. Trong bất kỳ trường hợp, đây là bốn cách thực hiện:

Đoán. Đó là từ mang nghĩa hơi thô, do đó bạn có thể dùng một từ thích hợp hơn. Những người không làm toán học thông thường đề cập đến nó như một “cảm giác chung”. Những nhà toán học đề cập đến nó như một “trực giác toán học”. Dù có tên nào thì nó cũng thường đưa ra kết quả sai, tuy nhiên cũng đủ tin cậy để thử.

2.Nhớ. Từ những ngày học trong nhà trường, bạn có thể nhớ đến cách nó sẽ trả lại kết quả như thế nào. Nếu trí nhớ không rõ ràng, nó sẽ trở thành một nửa nhớ, nửa “cảm giác”.

3.Phép nhân với 0. Chúng ta biết rằng 0 nhân với bất kỳ số nào cũng ra 0. Hiển nhiên, khi ta bắt đầu thực hiện phép nhân với 23 với hai số 0 ở cuối số 31,100, chúng ta vẫn được các chữ số0 cho đến khi gặp số 1 đầu tiên. Cộng với hai số 0 vẫn là 0. Chúng ta không nhận gì thêm từ số 0 cho đên skhi ta bắt đầu nhân đến các chữ 311 của 31,100 và sau đó nhận được kết quả tương tự như 311 nhân 23.

Sắp xếp lại các thành phần. Đó là phương pháp mà các nhà toán học đã dùng. Ý tưởng cơ bản là khi ta nhân kết hợp 2 số, nó không tạo sự thay đổi trong khi ita nhóm chúng lại, cho đến khi chúng ta dùng chúng trong mọi phép nhân. Lấy ví dụ, lấy 2 nhân 3 nhân 4. Thực hiện theo cách thông thường, ta nhân 2 với 3 là 6, sau đó nhân 6 với 4 được 24. Nhưng ta có thể, nếu muốn, nhân 3 với 4 trước. 2 nhân 3 nhân 4 trở thành 2 nhân 12, cũng đưa ra kết quả 24. Xa hơn, ta có thể sắp xếp lại, 2 nhân 3 nhân 4 tương tự như 2 nhân 4 nhân3, hoặc 8 nhân 3, cũng ra kết quả 24.

Bâygiờ áp dụng trong trường hợp 31,100 nhân 23. Chúng ta nghĩ theo cách 311 nhân 100 rồi nhân 23. Sắp lại các số, thành 311 nhân 23 rồi nhân 100. Nó bảo chúng ta thực hiện nhân 311 với 23, được kết quả như ở ví dụ trước, rồi nhân với 100. Bởi vì nhân bất kỳ số nào với 100 đơn giản chỉ là việc thêm 2 số 0 đằng sau số đó. Do đó ta ghi thêm 2 số 0 đằng sau kết quả vừa rồi, như đã đề cập.

Tiện lợi của phương pháp thứ tư là nó chỉ cho ta biết cách làm trong các trương hợp khác.Giả sử rằng hai chữ số 0 ở đằng sau số 23: Ta nhân 311 với 2,300 . Theo như cách 4, ta biết có hai số 0 ở đằng sau kết quả. Kết quả vẫn là 715,300. Nếu mỗi số đều có một số 0, phép nhân 3,110 với 230, cả hai số 0 này đều trả về sau kết quả, và ta vẫn có đáp số 715,300.

Quy tắc: Tổng hợp lại toàn bộ các số 0 ở đằng sau số bị nhân và số nhân và đặt chúng ở đằng sau kết quả. Sau đó thực hiện phép tính như bình thường với các số còn lại.

Lấy ví dụ, đây là ví dụ đầu tiên của chúng ta: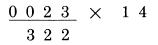

Giả sử chúng ta muốn nhân 230,000 với 140, vậy đáp án sẽ là ? Đơn giản chúng ta nhân như trong ví dụ trên, không quan tâm các số 0, sau đó tập hợp lại 5 số 0 ở hai số và viết chúng vào sau kết quả: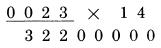

Đáp số là 32,200,000

Còn tiếp ...

School@net